
Subject Areas: Dynamical System

1. Introduction
We will consider a system  given by a locally compact Hausdorff space (phase space) X and λ-irresolute map
given by a locally compact Hausdorff space (phase space) X and λ-irresolute map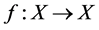 . A point
. A point 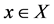 “moves,” its trajectory being the sequence
“moves,” its trajectory being the sequence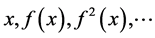 , where
, where 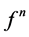 is the nth iteration of f. The point
is the nth iteration of f. The point  is the position of x after n units of time. The set of points of the trajectory of x under f is called the orbit of x, denoted by
is the position of x after n units of time. The set of points of the trajectory of x under f is called the orbit of x, denoted by . As a motivation for the notion of topological transitivity of
. As a motivation for the notion of topological transitivity of  one may think of a real physical system, where a state is never given or measured exactly, but always up to a certain error. So instead of points one should study λ-open subsets of the phase space and describe how they move in that space. If for instance the λ-type minimality of
one may think of a real physical system, where a state is never given or measured exactly, but always up to a certain error. So instead of points one should study λ-open subsets of the phase space and describe how they move in that space. If for instance the λ-type minimality of 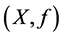 is defined by requiring that every point
is defined by requiring that every point  visits every λ-open set V in X (i.e.,
visits every λ-open set V in X (i.e.,  for some
for some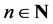 ) then, instead, one may wish to study the following concept: every nonempty λ-open subset U of X visits every nonempty λ-open subset V of X in the following sense:
) then, instead, one may wish to study the following concept: every nonempty λ-open subset U of X visits every nonempty λ-open subset V of X in the following sense:  for some
for some . If the topological system
. If the topological system 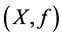 has this property; then it is called topologically λ-type transitive. We also say that f itself is topologically λ-transitive.
has this property; then it is called topologically λ-type transitive. We also say that f itself is topologically λ-transitive.
In this paper, new types of topologically λ-type transitive sets are introduced and studied. This is intended as a survey article on transitive sets in a system given by a λ-irresolute self-map on a topological space. On one hand it introduces postgraduate students to the study of new types of topological transitive sets and gives an overview of results on the topic; but, on the other hand, it covers some of the recent developments of mathematical science, technology, electronic and computer science. I introduced and defined a new type of transitive sets called λ-type transitive set and some of its properties are investigated. Relationships with some other types of transitive sets are given. I list some relevant properties of the λ-type transitive set. I have proved that every λ-type transitive set is transitive set but the converse not necessarily true. A topologically λ-type transitive set does not partition into nonempty λ-closed subsets. If A is a topologically λ-type transitive set, then there does not exist nonempty disjoint λ-closed subsets B and C of A such that![]() . Every topologically transitive set is nonempty λ-closed and invariant. The set of all λ-cluster points is called the λ-closure of A and is denoted by
. Every topologically transitive set is nonempty λ-closed and invariant. The set of all λ-cluster points is called the λ-closure of A and is denoted by ![]() A point x ∈ X is said to be a λ-interior point of a subset A ⊂ X if there exists a λ-open set U containing x such that U ⊂ A. The set of all λ-interior points of A is said to be the λ-interior of A and is denoted by
A point x ∈ X is said to be a λ-interior point of a subset A ⊂ X if there exists a λ-open set U containing x such that U ⊂ A. The set of all λ-interior points of A is said to be the λ-interior of A and is denoted by![]() , [1] - [3] .
, [1] - [3] .
2. Preliminaries and Definitions
To study the dynamics of a self-map ![]() means to study the qualitative behavior of the sequences
means to study the qualitative behavior of the sequences ![]() as n goes to infinity when x varies in X,
as n goes to infinity when x varies in X, ![]() is the position of x after n unit of time, where
is the position of x after n unit of time, where ![]() denotes the composition of f with itself n times.
denotes the composition of f with itself n times.
Definition 2.1. [4] By a topological system I mean a pair ![]() where X is a locally compact Hausdorff space (the phase space), and
where X is a locally compact Hausdorff space (the phase space), and ![]() is a continuous function. The dynamics of the system is given by
is a continuous function. The dynamics of the system is given by ![]() and the solution passing through x is the sequence
and the solution passing through x is the sequence![]() .
.
Definition 2.2. Let![]() , then the set
, then the set ![]() is called an orbit of x under f, so
is called an orbit of x under f, so ![]() is the set of points which occur on the orbit of x at some positive time, and the sequence
is the set of points which occur on the orbit of x at some positive time, and the sequence ![]() is called the trajectory of x.
is called the trajectory of x.
The set of limit points of the orbit ![]() is called the
is called the ![]() -limit set of x, and is denoted by
-limit set of x, and is denoted by ![]() A subset D of X is f-invariant if
A subset D of X is f-invariant if ![]() A non-empty closed invariant subset D of X is minimal, if
A non-empty closed invariant subset D of X is minimal, if ![]() for every
for every ![]() A point
A point ![]() is minimal if it is contained in some minimal subset of X.
is minimal if it is contained in some minimal subset of X.
For a point ![]() we say that f is λ-type open at x if for every open set U containing x,
we say that f is λ-type open at x if for every open set U containing x, ![]() for a subset
for a subset ![]() we say that f is λ-type open on A, if f is λ-type open at x for every
we say that f is λ-type open on A, if f is λ-type open at x for every ![]() Note that if f is open at x then it is λ-type open at x but not conversely.
Note that if f is open at x then it is λ-type open at x but not conversely.
Definition 2.3. [5] A function ![]() is called λ-irresolute if the inverse image of each λ-open set is a λ-open set in X.
is called λ-irresolute if the inverse image of each λ-open set is a λ-open set in X.
Proposition 2.4. Let ![]() be a map, where X, Y are λ-compact, second countable, Hausdorff spaces. If for each
be a map, where X, Y are λ-compact, second countable, Hausdorff spaces. If for each ![]() there exists a λ-open set U containing p such that
there exists a λ-open set U containing p such that ![]() is λ-irresolute, then f is λ-irresolute.
is λ-irresolute, then f is λ-irresolute.
Proof: Suppose that for every ![]() there exists a λ-open set U such that
there exists a λ-open set U such that ![]() is λ-irresolute. So there is a cover
is λ-irresolute. So there is a cover ![]() with this property. Consider a λ-open set
with this property. Consider a λ-open set![]() . Note that
. Note that ![]() so
so ![]() which is λ-open since f is λ-irresolute.
which is λ-open since f is λ-irresolute.
Definition 2.5. (1) Let ![]() be a topological space,
be a topological space, ![]() be λ-irresolute map, then the set
be λ-irresolute map, then the set ![]() is called λ-type transitive set if for every pair of non-empty λ-open sets U and V in X with
is called λ-type transitive set if for every pair of non-empty λ-open sets U and V in X with ![]() and
and ![]() there is a positive integer n such that
there is a positive integer n such that![]() .
.
(2) A topological system ![]() is λ-type chaotic if for every λ-open pair of not empty subsets
is λ-type chaotic if for every λ-open pair of not empty subsets ![]() there are a periodic point
there are a periodic point ![]() and
and ![]() such that
such that ![]()
Note that:
(1) Every λ-type transitive set is transitive set but not conversely.
(2) Every λ-type transitive map is transitive map but not conversely.
(3) The reason of the foregoing statements is that the map defined on the λ-transitive set is λ-transitive map. For more knowledge see [6] .
Definition 2.6 (1). Let ![]() be a topological space,
be a topological space, ![]() be λ-irresolute map, then the set
be λ-irresolute map, then the set ![]() is called topologically λ-mixing set if given any nonempty λ-open subsets
is called topologically λ-mixing set if given any nonempty λ-open subsets ![]() with
with ![]() and
and ![]() then
then ![]() such that
such that ![]() for all
for all ![]()
(2) A λ-closed set ![]() is called a weakly λ-mixing set of
is called a weakly λ-mixing set of ![]() if for any choice of nonempty λ-open subsets
if for any choice of nonempty λ-open subsets ![]() of A and nonempty λ-open subsets
of A and nonempty λ-open subsets ![]() of X with
of X with ![]() and
and ![]() there exists
there exists
n ∈ N such that ![]() and
and ![]()
Proposition 2.7. If A is a weakly λ-mixing set of![]() , then A is a λ-type transitive set of
, then A is a λ-type transitive set of![]() .
.
3. λ-Type Transitive Sets and Topological λr-Conjugacy
In the present section, I will introduce and define λ-type transitive sets. I will study some of their properties and prove some results associated with these new definitions. Some properties and characterizations of such sets are investigated.
A homeomorphism is a bijective continuous map with continuous inverse. More explicitly, to say that “a bijective mapping f of X onto Y is a homeomorphism” means that “![]() is open if and only if
is open if and only if ![]() is open”.
is open”.
Definition 3.1. A function ![]() is called λr-homeomorphism if f is λ-irresolute bijective and
is called λr-homeomorphism if f is λ-irresolute bijective and ![]() is λ-irresolute. More explicitly, to say that “a bijective mapping f of X onto Y is λr-homeomor- phism” means that “
is λ-irresolute. More explicitly, to say that “a bijective mapping f of X onto Y is λr-homeomor- phism” means that “![]() is λ-open if and only if
is λ-open if and only if ![]() is λ-open”.
is λ-open”.
Definition 3.2. Two topological systems![]() ,
, ![]() and
and![]() ,
, ![]() are said to be topologically λr-conjugate if there is λr-homeomorphism
are said to be topologically λr-conjugate if there is λr-homeomorphism ![]() such that
such that ![]() I will call h a topological λr-conjugacy.
I will call h a topological λr-conjugacy.
Then I have proved some of the following statements:
1) The maps f and g have the same kind of dynamics.
2) ![]() is a topological λr-conjugacy.
is a topological λr-conjugacy.
3) ![]()
4) A set B is λ-mixing set if and only if ![]() is λ-mixing set.
is λ-mixing set.
5) A set B is weakly λ-mixing set if and only if ![]() is weakly λ-mixing set.
is weakly λ-mixing set.
Proposition 3.3. If ![]() are λr-conjugated by the λr-homeomorphism
are λr-conjugated by the λr-homeomorphism ![]() then for all y ∈ Y the orbit
then for all y ∈ Y the orbit ![]() is λ-dense in Y if and only if the orbit
is λ-dense in Y if and only if the orbit ![]() of h(y) is λ-dense in X.
of h(y) is λ-dense in X.
Proof: Suppose that ![]() are maps λr-conjugate via
are maps λr-conjugate via ![]() such that
such that ![]() , then if for all y ∈ Y the orbit
, then if for all y ∈ Y the orbit ![]() is λ-dense in Y, let
is λ-dense in Y, let ![]() be a nonempty λ-open set. Then since h is a λr-homeomorphism,
be a nonempty λ-open set. Then since h is a λr-homeomorphism, ![]() is λ-open in Y, so there exists
is λ-open in Y, so there exists ![]() with
with![]() . From
. From ![]() it follows that
it follows that ![]() so that
so that ![]() is λ-dense in X. Similarly, if
is λ-dense in X. Similarly, if ![]() is λ-dense in X, then
is λ-dense in X, then ![]() is λ-dense in Y.
is λ-dense in Y.
If h is not λr-homeomorphism but only λ-irresolute surjection (a semi-λr-conjugacy), then the orbit ![]() is λ-dense in Y implies the orbit
is λ-dense in Y implies the orbit ![]() of h(y) is λ-dense in X, but not conversely.
of h(y) is λ-dense in X, but not conversely.
Proposition 3.4. if ![]() are λr-conjugate. Then,
are λr-conjugate. Then,
(1) T is λ-type transitive subset of X ![]()
![]() is λ-type transitive subset of Y;
is λ-type transitive subset of Y;
(2) T is λ-mixing subset of X ![]()
![]() is λ-mixing subset of Y.
is λ-mixing subset of Y.
Proof (1).
Assume that ![]() are topological systems which are topologically λr-conjugated by
are topological systems which are topologically λr-conjugated by![]() .Thus, h is λr-homeomorphism (that is, h is bijective and thus invertible and both h and
.Thus, h is λr-homeomorphism (that is, h is bijective and thus invertible and both h and ![]() are λ-irresolute) and
are λ-irresolute) and ![]()
Suppose T is λ-type transitive subset of X. Let A, B be λ-open subsets of Y with ![]() and
and ![]() (to show
(to show ![]() for some
for some![]() ).
). ![]() are λ-open subsets of X since h is an λ-irresolute.
are λ-open subsets of X since h is an λ-irresolute.
Then there exists some n > 0 such that ![]() since T is λ-type transitive subset of X, with
since T is λ-type transitive subset of X, with ![]() and
and![]() . Thus (as
. Thus (as ![]() implies
implies![]() ).
).
![]()
Therefore, ![]() implies
implies ![]() since
since ![]() is invertible. So h(T) is λ-type transitive subset of Y.
is invertible. So h(T) is λ-type transitive subset of Y.
Proof (2).
We only prove that if T is topologically λ-mixing subset of Y then h−1(T) is also topologically λ-mixing subset of X. Let U, V be two λ-open subsets of X with ![]() and
and![]() . We have to show that there is N > 0 such that for any n > N,
. We have to show that there is N > 0 such that for any n > N, ![]()
![]() and
and ![]() are two λ-open sets since h is λ-irresolute with
are two λ-open sets since h is λ-irresolute with ![]() and
and![]() . If the set T is topologically λ-mixing then there is N > 0 such that for any n > M,
. If the set T is topologically λ-mixing then there is N > 0 such that for any n > M, ![]() So
So![]() . That is
. That is ![]() and
and ![]()
![]()
![]() for
for![]() ,
,![]() . Thus, since
. Thus, since![]() , so that,
, so that, ![]() , and we have
, and we have ![]() that is
that is ![]() So, h−1(T) is λ-mixing set.
So, h−1(T) is λ-mixing set.
Proposition 3.5. Let ![]() be a topological system and A be a nonempty λ-closed set of X. Then the following conditions are equivalent.
be a topological system and A be a nonempty λ-closed set of X. Then the following conditions are equivalent.
1) A is a λ-transitive set of![]() .
.
2) Let V be a nonempty λ-open subset of A and U be a nonempty λ-open subset of X with![]() . Then there exists
. Then there exists ![]() such that
such that![]() .
.
3) Let U be a nonempty λ-open set of X with![]() . Then
. Then ![]() is λ-dense in A.
is λ-dense in A.
Note that for any![]() ,
,![]() ; the nth inverse image of A.
; the nth inverse image of A.
Theorem 3.6. Let ![]() be topological system and A be a nonempty λ-closed invariant set of X. Then A is a λ-type transitive set of
be topological system and A be a nonempty λ-closed invariant set of X. Then A is a λ-type transitive set of ![]() if and only if
if and only if ![]() is λ-type transitive system.
is λ-type transitive system.
Proof:
Þ) Let ![]() be two nonempty λ-open subsets of A. For a nonempty λ-open subset
be two nonempty λ-open subsets of A. For a nonempty λ-open subset ![]() of A, there exists a λ-open set U of X such that
of A, there exists a λ-open set U of X such that![]() . Since A is a λ-type transitive set of
. Since A is a λ-type transitive set of![]() , there exists n ∈
, there exists n ∈
N such that ![]() Moreover, A is invariant, i.e.,
Moreover, A is invariant, i.e., ![]() , which implies that
, which implies that ![]() Therefore,
Therefore, ![]() , i.e.
, i.e.![]() . This shows that
. This shows that ![]() is λ-type transitive system.
is λ-type transitive system.
Ü) Let ![]() be a nonempty λ-open set of A and U be a nonempty λ-open set of X with
be a nonempty λ-open set of A and U be a nonempty λ-open set of X with ![]() Since U is a λ-open set of X and
Since U is a λ-open set of X and![]() , it follows that U ∩ A is a nonempty λ-open set of A. Since
, it follows that U ∩ A is a nonempty λ-open set of A. Since ![]() is topologically λ-type transitive system, there exists n ∈ N such that
is topologically λ-type transitive system, there exists n ∈ N such that ![]() which implies that
which implies that![]() . This shows that A is a λ-type transitive set of
. This shows that A is a λ-type transitive set of![]() .
.
4. Conclusions
There are the following results:
Proposition 4.1. Every topologically λ-transitive set is transitive set but not conversely.
Proposition 4.2. If ![]() are
are ![]() -conjugate. Then,
-conjugate. Then,
(1) T is λ-type transitive set in X if and only if ![]() is λ-type transitive set in Y;
is λ-type transitive set in Y;
(2) T is λ-type mixing set in X if and only if ![]() is topologically λ-mixing set in Y.
is topologically λ-mixing set in Y.
Definition 4.3. Let ![]() be a topological space and
be a topological space and ![]() be λ-irresolute map, then the set
be λ-irresolute map, then the set ![]() is called topologically λ-mixing set if, given any nonempty λ-open subsets
is called topologically λ-mixing set if, given any nonempty λ-open subsets ![]() with
with ![]() and
and ![]() then
then ![]() such that
such that ![]() for all
for all ![]()
Definition 4.4. A λ-closed set ![]() is called a weakly λ-mixing set of
is called a weakly λ-mixing set of ![]() if for any choice of nonempty λ-open subsets
if for any choice of nonempty λ-open subsets ![]() of A and nonempty λ-open subsets
of A and nonempty λ-open subsets ![]() of X with
of X with ![]() and
and
![]() there exists n ∈ N such that
there exists n ∈ N such that ![]() and
and ![]()
Proposition 4.5. If A is a weakly λ-mixing set of![]() , then A is a λ-type transitive set of
, then A is a λ-type transitive set of![]() .
.
Proposition 4.6. Let ![]() be a topological system and A be a nonempty λ-closed set of X. Then the following conditions are equivalent.
be a topological system and A be a nonempty λ-closed set of X. Then the following conditions are equivalent.
1) A is a λ-transitive set of![]() .
.
2) Let V be a nonempty λ-open subset of A and U be a nonempty λ-open subset of X with![]() . Then there exists
. Then there exists ![]() such that
such that![]() .
.
3) Let U be a nonempty λ-open set of X with![]() . Then
. Then ![]() is λ-dense in A.
is λ-dense in A.
Theorem 4.7. Let ![]() be topological system and A be a nonempty λ-closed invariant set of X. Then A is a λ-type transitive set of
be topological system and A be a nonempty λ-closed invariant set of X. Then A is a λ-type transitive set of ![]() if and only if
if and only if ![]() is λ-type transitive system.
is λ-type transitive system.