Theoretical Study of Continuous B-Cell Epitopes with Developed BP Neural Network ()
Received 31 May 2016; accepted 23 July 2016; published 26 July 2016

1. Introduction
Epitope, also called antigenic determinant, refers to specific structure site of antigen molecular which is recognized by specific effect molecules or T, B lymphocyte cells in immune response. B cell epitope is a linear segment or space conformation structure in antigen molecule, which can bind to B cell receptor (BCR) [1] . B cell epitopes are composed of continuous epitopes and discontinuous epitopes [2] , and only less than 10% are continuous [3] .
Accurate prediction of B cell epitopes is not only helpful for research on basic immunology but also is useful for development of epitope vaccine and immunotherapy of autoimmune disease [4] - [6] . It is difficult to predict discontinuous B cell epitopes for space three-dimensional structure and structure flexibility [7] , despite the fact that the discontinuous B cell epitopes are far more than the continuous ones. For now, methods to predict discontinuous B cell epitopes are mainly structure-based and combination of sequence and structure. Therefore current prediction focuses on the continuous epitopes. In recent years, methods including machine learning method are applied to improve prediction performance. In current work, the modified BP neural network was used to predict the continuous B-cell epitopes, and finally the predictive model for the B-cells epitopes was established to prediction of the SWISS PROT NUMBER: P08677, and the establishment of modified BP neural network provided a new method for studying some protein system.
2. Methods and Results
2.1. Mathematical Theory of the Prediction Model
BP neural network model, also known as “Back Propagation artificial neural network”, was used to predict B cell epitopes. The error between output response and expected output of learning signal is taken as instructor signal by the network to regulate the network connection strength. The learning process is completed through repeated regulation which achieves the minimum error. BP neural network is now the most widely used neural network, which uses the smooth activation function and has one or more hidden layers, with the neighboring layers fully connected by a weighting value. It is a feed forward neural network, which means that information under processing will move forward layer by layer. However, it learns the weight value based on the difference between the ideal output and the actual output, and then modifies the weighting value via back propagation. Figure 1 shows the topology of BP network.
In Figure 1, 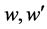 are weight value and
are weight value and 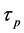 is the output of hidden layer. In this paper, the sample input vector is B cell epitope sequence which consists of amino acids. In amino acid sequence of a sample, each position possibly appears one of 20 different amino acids, so correspondingly 20 variables are introduced to denote 20 amino acids in some position of amino acid sequence [8] . For example, Ala is represented as “100000000000000 00000”, cys is represented as “01000000000000000000” and so on. This means each amino acid is equivalent to 20 neurons of the network input. The corresponding actual output is
is the output of hidden layer. In this paper, the sample input vector is B cell epitope sequence which consists of amino acids. In amino acid sequence of a sample, each position possibly appears one of 20 different amino acids, so correspondingly 20 variables are introduced to denote 20 amino acids in some position of amino acid sequence [8] . For example, Ala is represented as “100000000000000 00000”, cys is represented as “01000000000000000000” and so on. This means each amino acid is equivalent to 20 neurons of the network input. The corresponding actual output is , the error function is defined as:
, the error function is defined as:
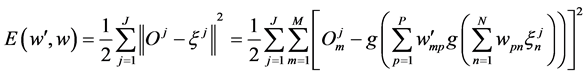 (1)
(1)
The determination of the weight matrix (learning process) should make the error function to achieve a minimum value. Usually during the learning process of BP network based on gradient descent principle, the information under processing will move forward layer by layer. While in the learning stage of network, the error back-
![]()
Figure 1. Back propagation neural network.
propagation algorithm is used to adjust the weight values layer by layer. Thus it is called Back Propagation algorithm [9] .
2.2. The Establishment of Prediction Model
The defects of common BP neural network algorithm are described as followed:
1) The slow convergence speed. Generally using BP algorithm to solve a network with four or five components will need thousands, even tens of thousands of cycles to achieve convergence, which makes it difficult to deal with massive data.
2) The easiness to fall into local minimum. BP algorithm can not guarantee the convergence value of network weight as the global minimization of error hyperplane. It is likely to be a local minimization, as shown in Figure 2.
3) The bad fault tolerance.
We can achieve the optimization in two respects:
a) Momentum method: Based on the back propagation method, proportional previous (t) weight change is added to every time (t + 1) weight change, which results in new weight change.
 (2)
(2)
Increase of momentum makes the weight and bias value adjust towards to the mean direction of error surface bottom. When 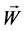 and b access into the flat area at the bottom of error surface, the convergence speeds up, namely
and b access into the flat area at the bottom of error surface, the convergence speeds up, namely 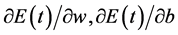 will become very small. So,
will become very small. So,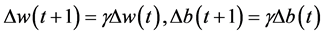 . This prevents
. This prevents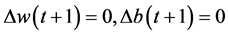 , which helps network jump out of local minima from error surface.
, which helps network jump out of local minima from error surface.
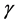 represents momentum coefficient. Considering convergence speed and jitter problems, momentum coefficient in this paper is 0.9.
represents momentum coefficient. Considering convergence speed and jitter problems, momentum coefficient in this paper is 0.9.
b) Adaptive learning rate: For specific problem, an appropriate learning rate is usually set according to experience or experiment. However even so, the learning rate which has good performance in early training often does not apply to the later training. Therefore, it is necessary to adjust learning rate. Variable learning rate back- propagation algorithm is described as followed: if the square error E (on the whole training set) increases after the weight is updated and is more than a percentage 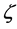 (a typical value of 1% ~ 5%), then the weight update is canceled, learning rate is multiplied by a factor
(a typical value of 1% ~ 5%), then the weight update is canceled, learning rate is multiplied by a factor 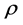 (
(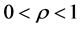 ), and momentum coefficient
), and momentum coefficient 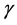 (if there is not) is set to 0. In this paper
(if there is not) is set to 0. In this paper![]() ,
,![]() . If the square error E decreases after the weight is updated, then the weight update is accepted, and learning rate is multiplied by a factor
. If the square error E decreases after the weight is updated, then the weight update is accepted, and learning rate is multiplied by a factor ![]() (
(![]() ). If it is set to 0, then return to the previous value; if the growth of E is less than
). If it is set to 0, then return to the previous value; if the growth of E is less than![]() , then the weight update is accepted, but learning rate remains same. If momentum coefficient was set to 0, then return to the previous value. Based on above three rules, they can be summarized as followed:
, then the weight update is accepted, but learning rate remains same. If momentum coefficient was set to 0, then return to the previous value. Based on above three rules, they can be summarized as followed:
![]()
Figure 2. The local and global minimization.
![]()
![]() (3)
(3)
According to the rules, the range of initial learning rate ![]() has great arbitrariness, but it is more prudent to use a smaller value.
has great arbitrariness, but it is more prudent to use a smaller value.
2.3. Setting of Model Parameters
1) Hidden layer number n = 1. By doing research on multi-hidden layers, we found that it was unnecessary to use multi-hidden layers which would make the network structure more complex and increase the computation greatly.
2) The initial learning rate η = 0.01. Although the setting of initial learning rate has great arbitrariness, it is more prudent to use a smaller value.
3) Activation function parameter β = 0.01. β represents the curve smoothness of activation function. The curve is more smooth with a smaller β. It decides the convergence speed with the learning rate.
4) Weight change mode: online mode, using this mode is due to the large number of sample data. If the batch mode is used, the number of training times will be far greater with excessive jitter problems. Also online gradient method can be considered as a stochastic perturbation of gradient method, which helps to jump out of local minima.
5) Target error E = 0.5. The training will be stopped when E is less than 0.5. Research found that smaller error setting would increase the running time greatly and cause over fitting.
6) The threshold is set 5. A threshold is used to identify epitope and non-epitope. By studying all thresholds from 0 to 10 with an interval 0.1, we found that sensitivity was almost equal to specificity when threshold was set 5.
7) Momentum factor α = 0.9. This value is set by synthetically considering convergence speed and jitter problems. When this value is less than 0.9, the convergence speed will be slow. When this value is greater than 0.9, the jitter problems will be excessive. It is related to the way how the network is prepared. When different coding is used, different momentum factor will be set based on the two factors.
2.4. Extraction and Preprocessing on Sample Data
Due to the shortage of sample data with only 700 positive samples and 700 negative samples in mostly database, the predictive result is not particularly good. In this paper, we mixed two data sets from Bcpreds [10] and ABCPred [11] , and each data set consists of 700 positive samples and 700 negative samples. By eliminating duplicate epitope, finally we got 2400 sample data for training. At the same time, the window length was 10, 12, 14, 16, 18 and 20 respectively. The best sample length was selected after comparing the predictive results.
2.5. Evaluation Indexes of Predictive Performance of the Model
The performance of the model is evaluated by using the parameters: sensitivity (SE), specificity (SP), positive prediction value (PV), negative prediction value (NV), accuracy (AC) and Matthews coefficient of correlation (CC):
![]() (4)
(4)
where TP is the number of predicted true positives, FP is the number of predicted false positives, TN is the number of predicted true negatives and FN is the number of predicted false negatives. A threshold (Th) is chosen to be compared with peptide’s predicted value. If predicted value is more than threshold, the peptide is considered as B cell epitope; otherwise, it is not considered as B cell epitope.
The performance of the prediction method is measured by ROC curves. An ROC curve is generated by computing SE and SP corresponding to all thresholds and taking (1-SP) as the X axis, taking SE as the Y axis. The area under ROC [12] curve (AUC) is a measure of prediction algorithm performance and has nothing to do with the threshold. Generally AUC = 0.5 indicates random prediction, AUC = 1 shows that all test data are predicted correctly, AUC > 0.7 is considered as significant prediction.
3. Results and Discussion
Figure 3 shows how the learning rate varies with the training step. It can be seen from Figure 3 that learning rate always adjusts self-adaptively. After reaching a peak value, it is quickly reduced to a very small value, and then increases. In the learning process, the peak value of learning rate in the beginning is much small, and then gradually increases with a nonlinear trend. This also shows the following advantages of using adaptive learning rate comparing with traditional BP network: small learning rate in the beginning can avoid the network concussion and ensure access to an accurate attraction domain; then greater learning rate can decrease learning time greatly and quicken the convergence process of network, while traditional BP network is difficult to do both.
As is shown in Figure 4, SE and SP equal curve describes random prediction with lack of correlation. The upper curve corresponds to the positive correlation of epitope position and prediction [12] . It can be seen from Figure 4 that our predictive results have good positive correlation. At the same time it also shows the performance of our model is significant, which can be used to predict epitopes.
By applying modified BP neural network method to predict samples with different length, we got predictive results as shown in Table 1. From the boldfaced lines in Table 1, the best length for B cell epitope is 18 amino acids. The B cell epitopes got from experiment mostly consist of 18 amino acids.
Circumsporozoite protein (SWISS PROT NUMBER: P08677) consists of 378 amino acids. Figure 5 shows the amino acid sequence of circumsporozoite protein. Circumsporozoite protein is surface antigen with immune- optimility on spore. On the infectious stage of malaria parasites, it is transmitted to the vertebrate by mosquito. The prediction model is applied to predict this antigen and only predict epitopes with a length of 18. Table 2 lists just a small part of the predicted results. The predictive value of a sequence, in the Table 2, indicates the possibility or degree elonging to positive or negative class. For example, if the predictive value is more larger than zero, the sequence gets more possibility belonging to positive class, otherwise more possibility of negative class. Our results include all experimental results given by the literature, which also shows the superiority of our model.
![]()
Table 1. Improved neural network B cell epitope-based different length of data table.
![]()
Table 2. Predicted circum sporozoite protein get results.
![]()
Figure 5. The sequence of the circum sporozoite protein.
4. Conclusion
By modifying the old neural network based on additional momentum method and adaptive learning rate, we estimated the neural network prediction model for identifying continuous B cell epitopes correctly. The simulation shows that for the boldfaced lines, the best length for B cell epitope is 18 amino acids among predicted samples, and sensitivity (SE) and specificity (SP) equal curve describe a good positive correlation. Noted that using artificial neural network to predict B cell epitopes is based on a large number of experimental data, and our results were in well agreement with experimental data. Therefore, modified artificial neural network method can provided exact identification of B-cells epitopes and give effective prediction for protein system.
Acknowledgements
This work was supported by Research Project of Education Department of Heilongjiang Province (Grant No.: 12543077) and the science and technology research projects of Jiamusi university (L2011-022).
NOTES
![]()
*Corresponding authors.