
Subject Areas: Philosophy

1. Introduction
Currently, there is debate concerning the possibility of eventually having artificial machines with natural intelligence. Would these machines exceed human intelligence? Should they? This paper explores a wide range of issues in order to get an idea of where to start the research regarding the safety on these potentially intelligent machines. There is a lot of good that can be achieved through artificial intelligence, but there are also issues regarding humanity’s safety that need to be addressed.
The analysis (including also some forms of synthesis) presented here considers the implications of the nature of the universe and ponders on questions such as: what was before the beginning of the big bang? What it means to have a beginning for the universe? How can destiny and free will coexist?
The concepts of nothingness and everythingness are carefully considered showing that their mathematical equivalences (zero and infinity, respectively) do have some incongruences. Although the arguments cannot prove or disprove the existence of God, arguments are made which seem to suggest the actual existence of God.
Computer experiments concerning cellular automata are thoroughly carried out and their relation to the very nature of the universe in which we live are carefully considered and discussed. The answers to the questions put forward derive in interesting conclusions concerning how it would be “safe” or “not safe” when building an artificial consciousness.
2. Finiteness and discreteness of the Universe
The first set of concepts to consider is derived from the nature of the universe. First of all, is the universe finite or infinite? It is common understanding in science that the universe originated at the big bang (Hawking [1] [2] ; Penrose [3] ; Reeves et al. [4] ), which happened approximately thirteen to fifteen thousand millions years ago (Sagan [5] ). Thus, the universe had a beginning. It is a peculiar beginning because it is considered that the big bang created both space and time. What was before the big bang? The obvious answer by following the principle known as Occam’s razor (or Ockham’s razor based on the name of the author of the principle created in the fourteenth century A.D.) is nothingness (Ockham [6] ).
Also, is the universe continuous or discrete in its nature? Following the reasoning of Zeno’s paradox (Malcolm [7] ), it can be concluded that the universe is discrete in nature. Thus, if there is one meter between two people, and if the first person tries to reach the second person by successively dividing the distance between them in half, and if there is no limit to this successive divisions, then the first person would never reach the second person. However, it is common knowledge that it is possible for anyone to reach anybody or anything else. Thus, the universe must be discrete in its spatial nature. Also, matter and energy, which occupy these discrete spaces, must be discrete in nature.
Consequently, if matter and energy evolve through time in a discrete space, they must be changing places in a discrete way. Thus, there must also be discrete time frames in the universe. The latter means that the universe must be finite in nature because there is a finite amount of time since the beginning of the universe at the big bang event (up to approximately fifteen thousand million years ago) and since both space and time are finite, that means the size of the universe which has been expanding since its beginning must also be finite (Castro [8] ).
3. Destiny
For hypothetical purposes, consider an imaginary universe which contains only two spaces. Also, imagine there is only one particle of matter or energy in such universe. At time one, the particle could be in the up or the down position (21 = 2 combinations). At time two, the particle could have been in the up-up, up-down, down-up or down-down positions (22 = 4 combinations). At time three there are eight possible evolutions for such universe (23 = 8 combinations). For any given amount of finite time that has happened, there is a finite (even though may be large) number of possible evolutions for such universe1.
Let now expand the analogy to the actual universe. There are a very large number of discrete spaces in our universe. Also, there are a very large number of discrete chunks of matter or energy in our universe. How many possible combinations for the matter and energy of the universe are there since the beginning of the universe? The answer: a huge number. However, that number is finite. If one chooses to believe in God and assumes God was at the beginning of the universe creating it and accommodating all discrete chunks of matter and energy, it is clear that God had only a finite number of possible evolutions for the universe to happen. Thus, God cannot do whatever God wishes. God needs to choose one of the possible and finite numbers of evolutions for the universe, which means God is constrained in choice by the very nature of the universe being created. This explains why some bad things happen, despite assuming an all-loving and all-caring God. It is because God had no other choice. Choosing differently would mean other worse things may happen elsewhere. Even if one chooses not to believe in God and assumes some given accommodation at random for the beginning of the universe, the same argument applies.
The latter means that things are going to happen in a specific way, which has already been set in motion at the beginning of the universe. Thus, is the idea of destiny, that is, the idea that things have been pre-specified to happen at the beginning of the universe. But are we not in control of our own destiny in some other way? What about free will?
Keep in mind the quantum mechanics and uncertainty principle. In quantum mechanics, all matter and energy behave both like a particle and like a wave. When it is measured, it assumes a particle behavior. When it is not, it assumes a wave behavior (Halliday and Resnick [9] ). Thus, free will does exist, but it has to be considered as whether or not such free will is being measured. Put simply, if one takes a decision, it is no longer free to decide anything else. If one thinks something, it is no longer free to think anything else.
4. Nothingness and Everythingness
Consider for example the number zero. Let x be any real number; then Equation (1) applies. If x = 1, then for n = 0, the value of equation (1) is 1; for n = 1 the value is 0.1, for n = 2 the value is 0.01 and so on until there is an infinite number of zeroes after the decimal point such that the ratio becomes zero when n equals (tends to) infinity.
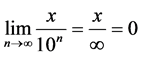 (1)
(1)
So far so good. But what is the value of 0/0? Consider equation (2). Although at the limit x = 0 and sin(x) = sin(0) = 0 and it would seem that we have the ratio 0/0, actual computations with values closer and closer to zero reveal that the ratio tends to 1. It is generally said that 0/0 is undetermined. How is that possible?
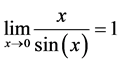 (2)
(2)
Consider now the expression shown in equation (3). As n increases, 10−n decreases down to the point where it equals zero at the limit when n®∞. The ratio 6/3 = 2 because 2 times 3 equals 6. However, it is not clear that ∞ times 0 equals x.
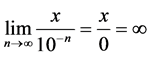 (3)
(3)
From Equation (1) there is x/∞ = 0 and from equation (3) there is x/0 = ∞. If it were valid to change the right side of the equations to the denominator and the denominator to the right side following a mechanization of algebra in either of the two expressions, both expressions would be equivalent. However, that is not a valid algebraic manipulation. Furthermore, it is not clear how 0 times ∞ would equal x and how ∞ times 0 would also equal x. It seems the mathematical concepts of zero and infinity are not entirely robust (Broiman [10] ; Landini [11] ).
As a result, it seems better to forget the mathematical equivalences typically assigned to nothingness and everythingness and try to think about them from a philosophical point of view (Durant [12] ; Magee [13] ). Conceptually, what is nothingness? Absolute nothingness (that is nothingness in the absence of both space and time) has nowhere to go. The same happens to everythingness, because everythingness occupies it all. Thus, it would seem as if both concepts are the same, at least when considering their philosophical properties.
5. The Act of Creation
The issue with having a big bang event at the creation of the universe where both space and time were created immediately suggests the question: what was before the big bang? The answer is nothingness (which according to the previous reasoning equals everythingness). There may be God before the big bang or not, but clearly God would be infinite in nature. Thus, it is possible for God in its infinite “mind” to calculate all possible evolutions for the universe (which thus far is regarded as finite in nature) and select the best one. The problem is what happens next.
According to the three scenarios possible for the future evolution of the universe it may be that the universe expands up to a limit when gravity would hold it back and would start to contract, in which case there would be a big crunch and possibly an eternal succession of creations and destructions. It may also be that the universe continues to expand at a constant rate forever. Or it may be that the universe continues to expand at an accelerating rate (Hawking [1] [2] ; Penrose [3] ).
But as it may be said: everything that has a beginning has an end. The beginning of the universe seems somewhat clear, but its end is not. The universe could not continue expanding forever because in such case it would also be infinite in nature and God could not compute an infinite universe. Maybe God considered the evolution of the universe up to a certain point and what happens after that is not God’s responsibility. Maybe that is precisely the nature of what is called in religion the apocalypse (Asimov [14] ).
6. Finiteness without Boundaries
There is, however, an interesting way of looking at the universe. Imagine for a moment that there is a universe in which beings exist in the two dimensional surface of a sphere. There could be triangles, squares, circles, polygons and so on. These beings could occupy the sphere and have their two-dimensional houses built on the surface of the sphere. Although clearly the sphere would be finite, such beings may not have any limits in their universe, because if one of them chooses to start moving in a straight line, it may never return to its original point of departure given the fact that the sphere is expanding. If there were two-dimensional galaxies on this sphere, as it expands, they would all separate from each other.
The same could be said happens in our universe, except that we exist (at least!) in a four dimensional arrangement of space and time in which we can be aware only of three dimensions at the same time, either having a one-instant impression of a three dimensional space or a two-dimensional “movie” unfolding as time evolves. This is precisely the concept found in the symbol of infinity (∞) or even further in a Moebius band (Cariani [15] ; Wood [16] ).
7. Body, Soul, Spirit and Free Will
It is necessary to consider the concepts of body, soul and spirit, which are typically regarded as religious concepts. Referring only to the Bible, the body is made of the material part of a human being. The soul and the spirit, on the other hand, are sometimes mixed as the same concept. However, the Bible says that God created man in God’s own image. But, what is God’s image? The Bible says God is spirit and the soul is what makes man alive (Asimov [14] ; King James Version Study Bible [17] ).
Using an analogy with a radio, it can be said that the physical components of the radio, including its transistors are the “body”, electricity is the “soul” which makes it alive and the “spirit” is the music that can be tuned from different radio stations. Consequently, the spirit seems to be an all-present characteristic related to God and, as such, infinite in its nature.
The latter means that the fact that humans have spirit, which is regarded as infinite, also implies that the human nature escapes the finiteness of the reasoning followed for the nature of the universe. Consequently, humans can have free will, since it is not possible, not even by God, to decide for humans because God cannot calculate the outcome of human’s infinite spirit. It is precisely in this way that both destiny and free will coexist.
8. Artificial Machines
Going further to the realm of machines other than biological ones, some scientists are now saying that artificial machines with natural intelligence are inevitable (Franklin [18] ; Minsky [19] ; Moravec [20] ; Turing [21] ; Kurzweil [22] [23] ), while others have said they are not inevitable (Searle [24] [25] ). But what would the nature of such machines be? Would they have free will? (That is, would it be its nature to be finite or infinite?)
In computer science there is something called pseudo-random numbers. These numbers are sequences that never repeat up to a certain point, called the size of the pseudo-random number generator (Coss Bu [26] ). If the decisions a machine take are based solely on pseudo-random numbers, then it is possible in theory to construct an even larger machine that could accurately predict the behavior of such machine. In such case, the machine would have no free will.
However, if the behavior of the machine is based on truly random numbers, then the machine would have free will and its actions would be unexpected. How could such machine be assigned truly random numbers? One way would be to utilize an algorithm capable or calculating all the successive digits of an irrational number. However, the existence of such algorithm is dubious. Another way would be to link the parameters of the pseudo random number generator to some physical property of the universe, such as the resistance of the machine’s transistors every now and then (Halliday and Resnick [9] ). The fact that the spirit permeates the universe means that in such case it would be virtually impossible to create a second machine, no matter how large and complex, to predict the behavior of the first machine. Theoretically, such behavior-predicting machine should have at least the size of the entire known universe.
9. Testing
When experimenting with one-dimensional cellular automata displayed on a two-dimensional screen having time being the second dimension (Wolfram [27] ), it is possible to see different types of cellular automata. It would be equivalent to work with Mandelbrot sets fractals or other fractals (Stevens [28] ), but fractals are much more difficult to implement in a thorough revision.
The drawing screen is 256 pixels in width and 512 pixels in height. Furthermore, the horizontal dimension is X and the vertical dimension is Y. The ranges of allowed values for X and Y are (0, 255) and (0, 511), respectively. Thus, XMin = 0, XMax = 255, YMin = 0 and YMax = 511.
The cellular automaton is a one-dimensional being existing in a two-dimensional world (a “plane” image). The horizontal dimension displays the population of cellular automata (pixels; either black or white) and the vertical dimensional displays time, that is, the evolution of the population of cellular automata as time goes by, where each time interval is represented by a new line of pixels in the vertical dimension. Although the image is plane, in the actual implementation, the cellular automata rules are applied as if the right boundary where connected with the left boundary, thus making this “universe” a cylinder, unbounded in the one-dimensional existence of the cellular automata. The “universe” starts with a single black pixel at the rightmost position of the plane (X = 255 and Y = 0). Then, each new line is drawn based on the previous line by considering the values (1 for black and 0 for white) of the pixel at the left, the pixel at the center and the pixel at the right position in the previous line of the current line being drawn. In the case of the leftmost pixel, the “left” position is in fact the rightmost position and in the case of the rightmost pixel, the “right” position is the leftmost position. Thus, the rules for each cellular automaton are applied as if the “universe” where cylindrical. Since there are three possible values (either 1 or 0) for each position, there are 23 = 8 possible combinations of values for the previous line when each new line is being produced. Also, there are 28 = 256 different rules to be applied. The evolution of the cellular automata can be of four possible kinds: 1) blank; 2) one cycle; 3) repetitive and 4) complex.
The very last population of cellular automata is scored in order to measure its complexity. Let bj (either 1 or 0) be the value of the cellular automaton at position j for the last line (Y = 511), where j = 0, ∙∙∙, 255. The black score (B) is the percentage of black cellular automata, and the white score (W) is the percentage of white cellular automata, as indicated by Equations (4) and (5), respectively. Notice that because of their definition, W = 1 − B, where B = 0, ∙∙∙, 1 and W = 0, ∙∙∙, 1, as indicated byequation (6).
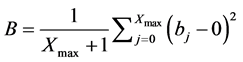 (4)
(4)
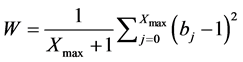 (5)
(5)
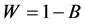 (6)
(6)
The combined score, C, is given by Equation (7). Notice that C cannot be higher than 0.25, because it is the result of multiplying two numbers between 0 and 1, and as indicated by Equation (6), the sum of these two numbers is 1. Thus, the maximum value for the multiplication of B and W occurs when both numbers are 0.5, and the result of multiplying 0.5 times 0.5 is 0.25. Dividing C by 0.25 and then multiplying it by 10 would yield a score value (S) between 0 and 10, as shown in Equation (8). Notice that a perfect score would only occur in a gray pattern such that the values are alternating. Consequently, a perfect score is not indicative of a truly complex pattern, but a score very close to ten may be indicative of a complex pattern.
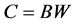 (7)
(7)
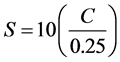 (8)
(8)
A cellular automaton is represented by a single pixel on a given line of length (width) 256 pixels and height given by the number of time intervals simulated. A black pixel (1 or true) represents a cellular automaton with a true value and a white pixel (0 or false) represents a cellular automaton with a false value. The first line (time 0) is all white pixels except for one black pixel at the rightmost corner. Although the height equals 512 pixels, it is possible by using the extended version of the software developed to test as many times as required by successively simulating more and more time intervals. Each new line is calculated by using the previous line. For any given pixel at position p (where p = 0, ∙∙∙, 255) at time t (where t = 0, ∙∙∙, 511, and so on), it is possible to calculate the cellular automata at time t by using the cellular automata at time t − 1. Thus, the pixel at the top left position, top position and top right position of cellular automaton at time t − 1 and position p is checked in order to determine whether the cellular automaton at position p and time t should be a black or a white pixel. Since there are three pixels to check, there are 23 = 8 different combinations of possible values to be found: 111, 110, 101, 100, 011, 010, 001, and 000. Also, since there are 8 different combinations of settings to consider, there are 28 = 256 different rules possible. Figure 1 illustrates rule 31: 11100001.
10. Results
Each and every possible rule is tested, and they are classified based on the type of pattern it shows. It is possible to have blank patterns, one cycle patterns, repetitive patterns, and complex patterns.
What it is being looked for are patterns that show inherent beauty and also patterns that do not repeat themselves. Although one cycle fractals may be beautiful, after an impressive drawing, the cellular automata fade to nothingness. There are cellular automata showing a repetitive sequence of triangular fractals (rule 95: 10100001, rule 106: 10010110, rule 127: 10000001, rule 130: 01111110, and rule 151: 01101001). Although these fractals show beauty, they do repeat after a given time and thus cannot be considered complex. Table 1 lists the scores obtained by all 256 rules analyzed. Generally speaking, complex rules tend to have a high score. Candidate complex rules are underlined and in bold font.
Blank are either all-white or all-black screens. One cycle displays are usually triangular fractals having one iteration only. Repetitive are typically diagonal or vertical lines (with a very low score) or grid-like or some other simple pattern (in some cases with perfect score), although sometimes there is a beautiful repetitive triangular fractal pattern (with or without a good score depending on the cutting point of the last line).
On the other hand, complex displays are the rare cases were it seems there is a beautiful pattern that does not repeat as time goes by (typically with a very high although not perfect score). Due to the complexity of these patterns, further analysis was required in order to see how the pattern progresses by considering more time (that is, additional lines on the vertical dimension in the form of additional displays). Table 2 and Figure 2 illustrate the respective percentages of patterns obtained after classifying them in blank, one cycle, repetitive and complex.
![]()
Figure 1. Cellular automaton checking for rule 31 (11100001).
![]()
Table 1. Scores for all 256 rules possible.
Note: Underlined and boldfaced rules are complex in nature, that is, non-repetitive patterns that show inherent beauty.
Notice that patterns that initially seem complex, such as rule 146 (see Figure 3(a)), after careful analysis turn out to be repetitive (see Figure 3(b)), whereas other patterns truly show complexity or at least it is not easy to identify where the repetitions begin and end.
Complex patterns that turned out to be repetitive correspond to rules 63 (11000001), 119 (10001001), 132 (01111100), and 146 (01101110). A very beautiful pattern that would seem it is repetitive at first impression (see Figure 4), after a considerable number of iterations shows itself as very complex and non-repetitive (see Figure 5).
The patterns that do have inner beauty and are also complex and not repetitive are rules 31 (11100001), 87 (10101001), 107 (10010101), 121 (10000111), 155 (01100101), 167 (01011001), 170 (01010110), 181 (01001011), 183 (01001001), 211 (00101101) and 226 (00011110). In particular, pattern rule number 183 is not only complex, not repetitive and beautiful, but also symmetrical.
![]()
![]() (a) (b)
(a) (b)
Figure 3. Apparent complex pattern for rule 146: 01101110. (a) Initial complex pattern; (b) repetitive pattern after several iterations.
![]()
Figure 4. Initial pattern corresponding to rule 31: 11100001.
![]()
Figure 5. Rule 31 after several iterations showing non-repetitive complexity and beauty.
11. Discussion and conclusion
Moravec [20] argues that the human brain has an information processing speed of about 100 million of millions (1014) instructions per second, each instruction per second being equivalent to carrying one elemental sum per second. However, the problem of building an artificial machine with natural intelligence is not on the processing speed. The Chinese supercomputer Tihane-2 (Tsay [29] ), processes information at the incredible speed of 33.86 petaFLOPS (peta Floating Point Operations per Second), that is 33.86 thousand millions of millions (3.386 × 1018) floating point operations per second, clearly faster than the information processing speed of the human brain. Then, why are we not aware of the existence of several conscious machines? The answer seems to be the fact that the way a supercomputer processes information is greatly different from the way a massively parallel supercomputer operates.
Tononi [30] explains that networks are the ideal way for building a conscious machine. Even if not all nodes are used at any given time, the fact that the nodes are there does provide information processing power. Kurzweil [23] goes further by arguing that the way the brain neocortex is organized is in repetitive and linear arrangements. Thus, there is an alternative to conscious machines in supercomputers, the configuration of mobile devices. It is reported that in 2014 Facebook reached 1230 million active users, and of those, 945 million are mobile (Impulso Negocios [31] ). It is supposed that mobile users have their device (namely a cellular phone) turned on all or almost all the time. If the Facebook application is configured to operate even when it is not being used, could it be possible to build an artificial machine with natural intelligence using such infrastructure?
Let consider this issue. A typical personal computer processor processed information at a speed of approximately 3 GHz, that is, three thousand millions operations per second. If it is supposed that the processor of a typical mobile device processes information with a speed 10% of a personal computer processor and that it can be used 10% of the capacity of the mobile processor without impairing the performance of the mobile device, there would be 3,000,000,000 × 0.1 × 0.1 = 30,000,000 operations per second per mobile device. On the other hand, if we consider the 100 million of millions operations per second the human brain is capable of and divide that by the 945 million mobile devices available, then the network of Facebook mobile applications would have to perform 100,000,000,000,000/945,000,000 ≈ 105,820 operations per second per mobile device. Comparing this minimum requirement with the estimated processing capacity of 30,000,000 operations per second per mobile device, it is clear there is the potential for creating a highly intelligent artificial machine with natural intelligence (it should actually be super-intelligent). It is just a matter of finding the right kind of processing between mobile devices needed. However, Facebook may not operate in such way as to be actively computing the conscious machine operations even if the application is not being used. Another application could be created for such purpose. This application would require having at least 100,000,000,000,000/30,000,000 ≈ 3,333,333 devices (not 945 million Facebook has reached) with the specially designed software that processes the intelligent machine functions when it is not active. Some kind of network game could be the ideal candidate. Clearly, the more mobile devices properly linked, the greater the intelligence potential this hypothetical conscious machine would have. Consequently, it seems it is merely a matter of time before such conscious machine is built.
There are 256 different positions for each cellular automaton and in each position there are two possibilities for each cellular automaton to exist in (black or white, that is, 1 or 0). Thus, there are 2256 possible combinations for the artificial universe of cellular automata studied to be in. Although that is a very large number, it is still finite, which means that it is not possible for anything to happen. There are a limited number of things that can happen. Also, after a maximum of 2256 time iterations, this universe would necessarily have to start repeating itself, since cellular automata that have already happened would appear again. The idea of destiny is clear in this artificial universe, since once a given rule is set, the artificial universe would start to unfold in a pre-specified manner. Free will for the cellular automata would exist if instead of blindly following the rule, some truly random transitions are allowed to occur every now and then. Thus, the combination of destiny and free will would create an artificial universe in which anything could happen.
It is possible to argue with certain degree of certainty that everything that has happened after a certain point in time called Plank time (Halliday and Resnick [9] ), which equals 5.38 × 10−44 seconds after the big bang, by merely using known scientific principles based on the idea of evolution (Reeves et al. [4] ) can be known by science. Clearly, no matter how small the Plank time interval is, it would not be impossible for an infinite God to work God’s “magic” within this time interval. It is even possible to further argue a transition from biological evolution to technological evolution in which biology and technology start to merge going towards the ideal of what God means (infinite creativity, infinity knowledge, infinite beauty and so on) as discussed by Kurzweil [22] [23] .
There is no clear evidence on the existence or non-existence of God. Even though the fact that there has to be something before the big bang, it could be argued that such something is nothingness, not everythingness (the latter being God). It could be that the fact that nature’s laws are so precisely tuned so that the universe could have evolved as it has could be due simply to the fact that we would not exist otherwise to ponder on these issues, which is called the anthropic principle (Hawing [1] ; Penrose [3] ; Reeves et al. [4] ). On the other hand, the argumentative need to have something before the big bang seems to incline the balance towards the existence of God. Nevertheless, the duality destiny and free will is rather intriguing.
The experiments carried out with cellular automata show that a relatively small percentage of such “creations” do show beauty and complexity. It also illustrates how in a given setting, it is possible to simply choose the right rule and then let the “universe” unfold forever. Whether choosing such rule is due to God or to the fact that our universe is one of many possible universes and the idea that the rules of nature are so precisely tuned to our own existence may be due to the anthropic principle needs considering. Nevertheless, an infinite or even some given number of alternative universes in which in most cases these universes would be wasted seems to go against the idea of the Ockham’s razor principle (Ockham [6] ). It would be simpler to assume the existence of just one universe and given the need to “choose the rule” for our universe, also to assume there is one God.
Considering a technological consciousness, if we are afraid of what it might decide, it would be recommended to simply make sure its decisions are not based on a truly random behavior. Such machine could be incredibly complicated, but ultimately predictable in any case. However, if we decide to provide such machine with free will under the form of a truly random basis for its behavior, we would be truly playing God and would have to be prepared to accept the consequences of such action. Alternatively, we, as a civilization, may choose to go through the “safe road” of Artificial Intelligence called Good Old Fashioned Artificial Intelligence (GOFAI), such that there would be an artificial machine for each need, not a single (or many) artificial machines with natural intelligence with the power to evolve itself (or themselves) towards increasing creativity, knowledge and beauty, because the latter would be to let machines get closer to God instead of humanity. Or maybe, biology and technology will fuse. Only the future can tell.
NOTES
![]()
1It is curious that at time zero, which would mean no space, no time and perhaps no energy, the total number of possible combinations would be 20 = 1.