Interrelations between Mathematics and Experiment in the Present Structure of Quantum Electrodynamics ()
Received 4 December 2015; accepted 18 December 2015; published 22 December 2015
Subject Areas: Theoretical Physics
1. Introduction
The variational principle plays a fundamental role in the present structure of theoretical physics. Thus, in their celebrated textbook [1] Landau and Lifshitz demonstrate how this principle can be used for the construction of classical electrodynamics. Modern presentations of Quantum Field Theory (QFT) also take the variational principle as the basis of the analysis (see e.g. [2] [3] ).
The variational principle is certainly a powerful element of theoretical physics. However, there is no guarantee that all its applications are perfect. Probably the most well known problem is the phenomenon of infinitely large quantities that are obtained in Quantum Electrodynamics (QED). This problem is now treated by a procedure called renormalization (see [4] , pp. 269, 390; [5] , p. 284). Here the calculations yield physically unacceptable infinitely large quantities. Each of these quantities is removed with the help of another infinitely large quantity and it is argued that the physically meaningful result is an appropriate finite difference between these infinities. The mathematical aspect of renormalization is doubtful. For example, Wikipedia, which is based on the present consensus, states in its renormalization item: “It seemed illegitimate to do something tantamount to subtracting infinities from infinities to get finite answers.” Obviously, the situation would have been much better if the correct results are obtained directly without the need to apply renormalization.
Renormalization is certainly a problematic issue. Thus Dirac said that it has an “illogical character” [6] , whereas Feynman called it “a dippy process” [7] . By contrast, during the last 100 years no serious physicist has used such words with respect to any part of special relativity. This is yet another indication of the existence of questionable aspects of renormalization.
On top of these matters, one should not be quite sure about the veracity of the common belief concerning QED’s extraordinary experimental success. Indeed, it is interesting to note that a large disagreement has recently been found between QED calculations of the proton’s charge radius and measurements of this quantity with muons [8] . Here the amazing QED precision of seven or more decimal digits deteriorates to just one decimal digit.
The second issue is the construction of the electromagnetic fields energy-momentum tensor from the fields’ Lagrangian density (see [1] , pp. 82-89; [9] , pp. 601-608; [10] , pp. 120-122). Here the analysis yields an unacceptable expression which is corrected by adding to it a specific term. Thus, the following question arises: Why other theoretical elements of electrodynamics like Maxwell equations and the Lorentz force are directly obtained from an application of the variational principle whereas the construction of the fields’ energy-momentum tensor needs to be corrected by a specific trick? It can be stated that, like the case of QED’s infinities, the situation would have been much better if the correct result is obtained directly without the need to apply a further trick.
The present work proves that these apparently unrelated problems stem from the same element which is the structure of the electromagnetic part of the Lagrangian density. The work uses standard notation and a system of units where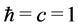 . The second section discusses interrelations between physical data and mathematics. QED’s infinities and the fields energy-momentum tensor are discussed in the third section. Fundamental properties of electromagnetic fields are derived in the fourth section and they prove that the presently used electromagnetic term of the Lagrangian density is unjustified. The last section points out how the problems may be settled.
. The second section discusses interrelations between physical data and mathematics. QED’s infinities and the fields energy-momentum tensor are discussed in the third section. Fundamental properties of electromagnetic fields are derived in the fourth section and they prove that the presently used electromagnetic term of the Lagrangian density is unjustified. The last section points out how the problems may be settled.
2. Interrelations between Physical Data and Mathematics
It is well known that mathematics plays a cardinal role in the structure of theoretical physics [11] . Interrelations between experimental data and mathematical expressions are discussed in this section.
A landmark in the progress of physics is the celebrated Galileo’s experiment where he dropped two balls from the Piza tower. Among other issues, this experiment demonstrates the crucial part of measurement in the structure of theoretical physics. This is however not the full story about the interrelations between experiment and mathematics in theoretical physics.
Successful physical theories have been constructed in the following steps. First, a not very large number of meaningful experimental data are used as a starting point. Hereafter, these data are called the fundamental data of the theory. Next, one introduces some postulates which are consistent with these data and serve as a basis for constructing the principal mathematical expressions of the theory. At this point mathematics takes over and it turns out that if the theory is correct then mathematical predictions are later confirmed by experiment.
Maxwell equations serve here as an illustration of this description. First, formulas of electromagnetic pro- cesses were known in Maxwell’s time. These formulas have been constructed on the basis of experimental data. In his attempts to use these formulas and create a system of partial differential equations he found that the equations describe a world where charge is not conserved. This is certainly inconsistent with the world as we know it. Thus, he added a term known as Maxwell displacement current to the equations (see [9] , pp. 217-219). In so doing, he has obtained a set of partial differential equations for the electromagnetic fields. From this point on, mathematics successfully predicts phenomena of classical electrodynamics. For example, a mathematical analysis of Maxwell equations proves that there are transverse electromagnetic waves that travel at the speed of light and this speed is the same in all inertial frames. This is a successful prediction of Maxwellian theory which paved the road to special relativity as well as to many technological achievements.
Analogous features can be found in the construction of special relativity and in that of quantum mechanics. By contrast, if the principal mathematical expressions of a given theory are inconsistent with its fundamental data then erroneous results may pop up from a mathematical analysis. This issue is discussed in the rest of this work.
3. Two Problems in Electrodynamics
In the progress of time the variational principle has acquired an important status in physical theories. This work discusses two electromagnetic theories: Classical electrodynamics which is derived from the variational principle (VE) (see [1] ) and quantum electrodynamics (QED). Problems of these theories are briefly described in this section.
Let us examine the VE construction of the energy-momentum tensor of electromagnetic fields. The present method of obtaining this quantity can be found in textbooks (see [1] , pp. 82-89; [9] , pp. 601-608; [10] pp. 120-122). This method is very briefly outlined as follows: Rely on the variational principle and apply the standard method of constructing the energy-momentum tensor to the electromagnetic fields Lagrangian density. The expression obtained 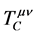 is called the canonical energy momentum tensor. It turns out that this expression is incorrect. The requirement of angular momentum conservation demonstrates this point. Indeed, a straightforward calculation proves that this requirement is satisfied if the energy-momentum tensor is symmetric, whereas the canonical energy-momentum tensor is not symmetric. In order to resolve this problem a divergenceless quantity is added to this tensor so that the required form
is called the canonical energy momentum tensor. It turns out that this expression is incorrect. The requirement of angular momentum conservation demonstrates this point. Indeed, a straightforward calculation proves that this requirement is satisfied if the energy-momentum tensor is symmetric, whereas the canonical energy-momentum tensor is not symmetric. In order to resolve this problem a divergenceless quantity is added to this tensor so that the required form  is obtained. This tensor is called the symmetric energy momentum tensor (see [1] , pp. 86-89; [9] , pp. 601-606; [10] , pp. 120-122).
is obtained. This tensor is called the symmetric energy momentum tensor (see [1] , pp. 86-89; [9] , pp. 601-606; [10] , pp. 120-122).
One is likely to feel uneasy with this type of procedure which uses a specific patch for correcting a physical quantity which is derived from an important principle of theoretical physics. This kind of feeling is nicely described by Munoz [12] :
“Few things are more frustrating students than to be led through a long, formal argument only to be told at the end that the result obtained is incorrect and must somehow be fixed by an auxiliary procedure. This is particularly harmful if the formal argument involved turns out to be one of the mathematical cornerstones of modern physics. Unless the discussion includes a re-examination of the analysis to find out exactly what went wrong, the students will be left with the paradoxical feeling that a supposedly very general theorem produces unacceptable answers when applied to certain specific situations. Quite understandably, later on they will be reluctant to think about any physical problem in terms of the tools provided by such a theorem.
The case we have in mind is the typical derivation of the energy-momentum tensor for relativistic field theories. Most textbooks begin the discussion by writing down a Lagrangian and arguing that this Lagrangian must be invariant under a spacetime translation. The details of the derivation vary from text to text, but the end result invariably yields the energy-momentum tensor...”
Munoz continues and explains why attempts to correct  are physically unacceptable. However, for the purpose of this work it is enough to point out that a VE mathematical analysis yields a physically unacceptable result.
are physically unacceptable. However, for the purpose of this work it is enough to point out that a VE mathematical analysis yields a physically unacceptable result.
The second problem is related to the infinities of QED and the renormalization procedure which aims to overcome this unacceptable result [4] [5] . As stated in the Introduction, the present version of Wikipedia describes renormalization in the following words: “It seemed illegitimate to do something tantamount to subtracting infinities from infinities to get finite answers.”
It is interesting to note that Dirac and Feynman, who are two eminent QED figures, have denied the renormalization attempts to correct QED. Thus, Dirac has described renormalization as a procedure of an “illogical character” [6] . He continued and said: “I am inclined to suspect that the renormalization theory is something that will not survive in the future, and that the remarkable agreement between its results and experiment should be looked on as a fluke”. (The recent proton radius measurement which is mentioned in the Introduction supports this prediction of Dirac.) A similar approach has been expressed by R. P. Feynman, who has used a more colorful terminology and called renormalization “a dippy process” [7] . Feynman continued and stated: “I suspect that renormalization is not mathematically legitimate”. An analogous statement can be found in Ryder’s textbook (see [4] , p. 390). The author compares quantum divergences to classical ones and says: “In the quantum theory, these divergences do not disappear; on the contrary, they appear to get worse, and despite the comparative success of renormalisation theory the feeling remains that there ought to be a more satisfactory way of doing things.”
Here we see that two electrodynamic theories―the VE version of classical electrodynamics and QED―yield erroneous results. Both theories use the variational principle as a cornerstone and the electromagnetic Lagrangian density is a fundamental quantity. Interrelations between experiment and this structure of VE and QED are discussed in the next section.
4. Fundamental Properties of Electromagnetic Fields
Let us examine what experiment says about some fundamental properties of electromagnetic fields. The first issue is the difference between bound fields and radiation fields. Let us take the hydrogen atom, which is a quite simple system of a proton and an electron, and use it as our experimental device. It is well known that quantum mechanics provides an extremely successful description of the hydrogen atom. Therefore, the required experimental data can be readily taken from quantum mechanics textbooks [13] [14] .
The hydrogen atom ground state has an orbital angular momentum 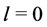 and an even parity. This system is stable and electromagnetic bound fields determine the interaction energy
and an even parity. This system is stable and electromagnetic bound fields determine the interaction energy
 (1)
(1)
where 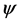 denotes the ground state wave function and
denotes the ground state wave function and  denotes the interaction operator. Hence, the operator of the electromagnetic fields that bind the electron to the proton has an even parity and an intrinsic angular momentum
denotes the interaction operator. Hence, the operator of the electromagnetic fields that bind the electron to the proton has an even parity and an intrinsic angular momentum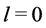 . (If the parity of
. (If the parity of  is odd then
is odd then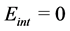 . The same result is obtained for the case where the angular momentum of
. The same result is obtained for the case where the angular momentum of  is not zero.) Therefore, electromagnetic bound fields have an intrinsic angular momentum
is not zero.) Therefore, electromagnetic bound fields have an intrinsic angular momentum ![]() and an even parity.
and an even parity.
Let us turn to the case of one photon transition between two states of the hydrogen atom. This process abides by well known selection rules. Here one finds (see [13] , p. 264; [14] , p. 466)
![]() (2)
(2)
where ![]() denote the orbital angular momentum of the initial and the final state, respectively. (Obviously, for
denote the orbital angular momentum of the initial and the final state, respectively. (Obviously, for![]() ,
,![]() .) Thus, one obtains the well known properties of the photon (namely, radiation fields): electromagnetic radiation fields have an intrinsic angular momentum (called helicity)
.) Thus, one obtains the well known properties of the photon (namely, radiation fields): electromagnetic radiation fields have an intrinsic angular momentum (called helicity) ![]() and an odd parity.
and an odd parity.
Conclusion 1: Bound fields and radiation fields are inherently different physical objects. Since electrodynamics conserves both angular momentum and parity, its theory must treat differently bound fields and radiation fields.
It should be pointed out that although the foregoing analysis of bound and radiation fields is carried out in the hydrogen atom rest frame, the results are valid in any Lorentz frame. Thus, for example, a transition from 2p to 1s is associated with radiation emitted by the system and a decrease of its energy. On the other hand, the ground state emits no radiation and the state’s self-energy is conserved. Evidently, if radiation is found in one inertial frame then this effect can be found in any other frame. Hence, a Lorentz transformation does not mix bound and radiation fields.
Let us examine the radiations emitted from two different sources. The interaction term of electrodynamics depends on the 4-potential of the electromagnetic fields ![]() and on the 4-current of the charged matter
and on the 4-current of the charged matter ![]() (see [1] , p. 78)
(see [1] , p. 78)
![]() (3)
(3)
It means that there is no direct interaction between electromagnetic fields. In particular, there is no direct interaction between radiation emitted from different sources. (Indirect interaction can be found in cases where the combined invariant mass of the two photons is more than 1.022 MeV, which is the sum of the electron and the positron mass.)
Conclusion 2: Radiation fields that are emitted from different sources should be treated separately.
Another experimental evidence pertains to the definition of the electric field. This is done by measuring the force which a given array of charges exert on a test charge (see [9] , p. 28). This definition means that the field of a given charge is defined by the force exerted on another charge. The well known problem of the 4/3 factor of the Lorentz transformation of the fields momentum of a point charge (see e.g. [15] ) indicates that self-interactions of the fields of a point charge are inconsistent with the theory.
Conclusion 3: The definition of the electric field says nothing on self-interactions between fields of an elementary point charge.
The theoretical work of constructing VE (see [1] ) and of QED ignores the inherently different attributes of these kinds of fields and combines all of them together. Thus, the primary expression of the analysis is the electromagnetic fields Lagrangian density. This quantity takes the form (see [1] , p. 86; [5] , p. 70)
![]() (4)
(4)
where ![]() is the tensor of the electromagnetic fields. Here
is the tensor of the electromagnetic fields. Here ![]() is the sum of all kinds of fields.
is the sum of all kinds of fields.
This form of the Lagrangian density certainly does not distinguish between bound fields and radiation fields nor between radiation fields emitted from two different sources. This issue leads to unacceptable results. For example, let us write the tensor of the electromagnetic fields as a sum of bound fields and radiation fields
![]() (5)
(5)
where the subscripts ![]() denote bound fields and radiation fields, respectively. Substituting (5) into (4), one obtains the following form of the Lagrangian density of electromagnetic fields
denote bound fields and radiation fields, respectively. Substituting (5) into (4), one obtains the following form of the Lagrangian density of electromagnetic fields
![]() (6)
(6)
As found above, the parity of bound fields is even whereas the parity of radiation fields is odd. Hence, the last term of (6) violates parity. This property is completely inconsistent with electrodynamics which is a parity conserving interaction.
Evidently, an analogous analysis shows that (4) contains a product of radiation fields emitted from two different sources. This product represents interaction which is not found in experiment. Furthermore, Conclusion 3 does not deny the possibility that the true Lagrangian density reflects only the interaction between fields of elementary pointlike charges. Thus, the corresponding Lagrangian density of bound fields takes the form
![]() (7)
(7)
where the indices ![]() run on fields of all charges of the system. Similarly, the charge-fields interaction is
run on fields of all charges of the system. Similarly, the charge-fields interaction is
![]() (8)
(8)
Hence, there are inconsistencies between experiment and the mathematical structure of the important elements (3) and (4) of VE and of QED. For this reason, it is not surprising to find that mathematics retaliates immediately. Thus, VE yields an unacceptable energy-momentum tensor whereas QED calculations yield the well known infinitely large quantities. Certainly, this states of affairs is inadmissible.
5. Concluding Remarks
The well known infinities of QED show that mathematics screams when stumbling upon something which is inherently wrong. An analogous result is obtained from the VE calculations of the electromagnetic fields energy- momentum tensor and from the 4/3 factor of the Lorentz transformation of the momentum of self-interaction of the fields of a point charge. The present work reveals the origin of the problem. The analysis which is shown in Section 4 proves the following conclusions:
1) Bound fields and radiation fields have different angular momentum and parity. It follows that they are inherently different physical objects. Since electrodynamics conserves both angular momentum and parity, its theory must treat differently bound fields and radiation fields.
2) Radiation fields that are emitted from different sources do not interact. Therefore, they should be treated separately.
3) The definition of the electric field says nothing on self-interactions between fields of an elementary point charge.
The fields part of the presently accepted form of the Lagrangian density (4) is inconsistent with these conclusions because it uses ![]() which is the sum of all kinds of fields. On the other hand, the form of the electromagnetic Lagrangian density (7) and (8) does not contain self-interactions of the fields of a point charge. Therefore, it looks like a promising basis for an inherently regular theory of electrodynamics. It means that this work indicates the way out of this dilemma: A correct theory should treat bound fields and radiation fields differently, separate between radiation fields emitted from different sources and use a Lagrangian density that represents only the interaction between different point charges. A successful and comprehensive realization of these ideas looks like a not very simple assignment.
which is the sum of all kinds of fields. On the other hand, the form of the electromagnetic Lagrangian density (7) and (8) does not contain self-interactions of the fields of a point charge. Therefore, it looks like a promising basis for an inherently regular theory of electrodynamics. It means that this work indicates the way out of this dilemma: A correct theory should treat bound fields and radiation fields differently, separate between radiation fields emitted from different sources and use a Lagrangian density that represents only the interaction between different point charges. A successful and comprehensive realization of these ideas looks like a not very simple assignment.