On Explanation of Polygons in Galilean Geometry to High School Students

Abdullah Kurudirek, Huseyin Akca

Tashkent State Pedagogical University, Tashkent, Uzbekistan.

DOI: 10.4236/oalib.1101391                

Abstract

In this paper, we have tried to indicate the own properties of polygons in Galilean geometry using the Affine concepts as well. The relationships between an angle and a side as well as the relationships between altitudes and medians concepts, and comparison of some special polygons have been examined carefully. In addition, the area concept has been mentioned. Finally, the paper was completed with a new idea, Theorem 6.

Keywords

Galilean Plane, Kinematic, Projection, Special Line, Support Line

Subject Areas: Geometry, Geometry Education

1. Introduction

Düzlemde, Galileo geometrisi Öklid geometrisinden vektör normu (uzunluğu) veya noktalar arasındaki mesa- fenin tanımlanış biçiminden dolayı ayrılır [1] . Bundan dolayı da Galileo geometrisindeki doğru, doğru parçası, doğruların paralelliği gibi Afin kavramlar Öklid geometrisinden farklı değildir. Bu birliktelik bize Galileo geometrisinde çokgenlerin de aynı Öklid geometrisindeki gibi tanımlanma imkanını vermektedir.

Galileo geometrisinde mesafenin tanımlanması, herhangi bir şekildeki çokgeni öğrenme imkanı verme- mektedir. Bundan dolayı, Galileo düzleminde öğrenilen çokgenlerin hiç bir kenarının özel doğrular üzerinde bulunmadığını baştan kabul edelim. Dolayısıyla da çokgenlerin ardarda gelen köşeleri özel bir doğru üzerinde olamayacağı sonucu ortaya çıkmış olacaktır [2] .

Galileo düzlemindeki üçgen ve ona ait elemanların özellikleri yeterli seviyede anlatılmış ve öğrenilmiş bulunmaktadır. Biz bunlardan en önemlisini (Şekil 1) alıp üzerinde çalışalım istedik. Şimdi Galileo düzleminde,

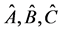kenarlarını ve iç açılarıda ile gösterilen bir 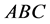üçgeni verilmiş olsun.

Şekil 1. Galileo düzleminde üçgen.

Burada üçgenin kenarları ve açıları arasında 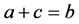ve eşitlikleri sağlanmaktadır. Kenarlar arasındaki ilişki sayesinde, Galileo geometrisinde eşkenar üçgenin olmadığını hemde açılardan dolayı üç açınında eş açılı bir üçgen oluşturamayacağını bizlere göstermektedir. Ama ikizkenar üçgenimiz mevcut ve onun tabanındaki açılarında birbirine denk olduğunu yine kolay bir ödev olarak öğrencilerimize bırakabiliriz.

Üçgendeki kenarortay kavramı da yine aslında Afin kavramı olduğu için Öklid geometrisindeki özellikleri

Galileo geometrisinde de geçerlidir. Yani üçgenin kenarortayı üçgenin kenarlarıyla bir noktada kesişir ve

oranında böler. Galileo geometrisindeki açı, Öklid geometrisindeki açı düşüncesinden tamamen farklıdır. Bu durum bize üçgendeki açıortayın Galileo geometrisinde yeni bir kavram olduğunu gösterir. Demek, Galileo geometrisindeki açıortay Öklid geometrisindeki üçgenin açıortayından ayrılmaktadır. Üçgenin yüksekliği ise Galileo geometrisinde kendisine ait özellikler göstermektedir.

2. Tanım

Galileo geometrisinde bir üçgenin yüksekliği diye üçgenin köşesinden çizilen özel doğrunun karşı kenar ile kesişmesinden oluşan özel doğru parçasına denir. Bu tanımda, Öklid geometrisindeki üçgenin yüksekliğinin noktadan doğruya kadar olan en kısa mesafe olması özelliği korunmaktadır. Ama yüksekliğin karşı kenara dik olması durumu şart değildir. Öklid geometrisindeki üçgen eşitliği şartlarından birinci ve ikincisi Galileo geome- trisinde de geçerlidir. Bu durumları aşağıdaki Teoremlerle hatırlayabiliriz.

Teorem 1.

Eğer bir üçgenin iki kenarı ve onlar arasındaki açıyla, ikinci üçgenin iki kenarı ve onlar arasındaki açı karşılıklı eşit olursa bu üçgenler kendi aralarında eşittirler.

Şekil 2. Eşit Üçgenler.

Teorem 2.

Eğer bir üçgenin kenarı ve ona komşu iki açıyla, ikinci üçgenin bir kenarı ve ona komşu açıları karşılıklı eşit olursa bu üçgenler kendi aralarında eşittirler.

Şekil 3. Eşit Üçgenler.

Bu Teoremlerin ispatı zor olmamakla beraber, yaygın bir şekilde okullarda geometri derslerinde öğretilmektedir. Esasen bu ispatlar Galileo geometrisindeki hareket konusunun özelliklerini öğrenme imkanı vermektedir.

Üçgenlerin kenarları arasında eşitlik şartı Galileo geometrisinde geçerli değildir. Kenarları ve açıları karşılıklı eşit olan üçgenlerin eşit olma şartı yoktur [2] . Bu durum aşağıda 4. ve 5. şekillerde açıkca görülmektedir.

Şekil 4. Üçgenlerin kenar ilişkisi.

Şekil 5. Üçgenlerin kenar ilişkisi.

Şimdi Galileo geometrisinde sade bir dörtgen olan paralelkenar ile tanışalım. Paralelkenarın karşılıklı kenar- ları ve karşılıklı açıları birbirine eşittir. Bu özelliğin Öklid geometrisinde de geçerli olduğu hemde mesafenin Öklid mesafesinin izdüşümü kavramı olduğu sonucu ortaya çıkar.

Teorem 3.

Karşılıklı köşeleri özel bir doğru üzerinde bulunan paralelkenar, Şekil 6 da gösterildiği gibi, eşkenar dört- gendir. Eşkenar dörtgenin köşegenleri birbirlerini ortalar.

Gerçekten de paralelkenarın eşkenar dörtgen olması için, onun bütün kenarlarının birbirine eşit olması gerek- mektedir. Çokgenin bir köşesinden çizilen iki kenarın denk olması için onların ikinci köşelerinin bir özel doğru üzerinde olması zaruri ve yeterli sebeptir. Buradan paralelkenarın köşegenlerinden birinin özel doğru üzerinde bulunması fikri ortaya çıkar. İkinci köşegeni ise özel doğru üzerinde bulunmaz. Özel doğru, özel olmayana dik- tir buda teoremin geçerli olduğunu gösterir.

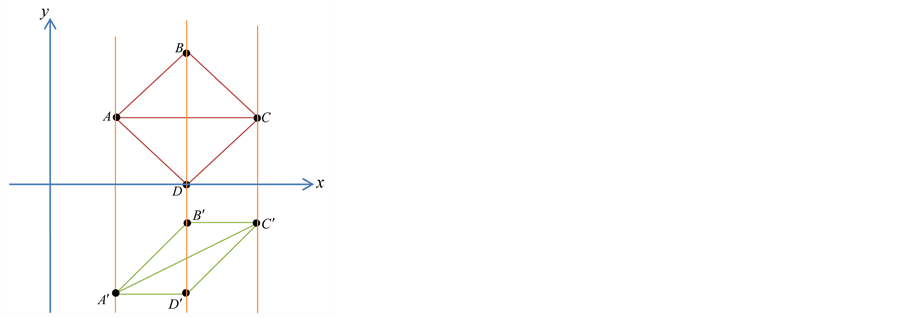
Şekil 6. Eşkenar dörtgen & Paralelkenar.

Ne yazık ki, Galileo geometrisinde dikdörtgen ve kare düşünceleri genelleştirilememektedir. Galileo geome- trisinde her hangi 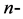dışbükey çokgeninin iki özel doğrudan oluşan dayanak doğruları ve 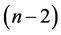tane kenar- ları özel doğrulara oranla her çeşit yarım düzlemde yerleşmiş köşeleri vardır. Bunlar sırasıyla dayanak köşe ve dayanak doğruları diye adlandırılır.

Teorem 4.

Galileo geometrisinde çokgenin (Şekil 7) dayanak köşeleri açılarının ölçüleri toplamı diğer köşelerin açı ölçülerinin toplamına eşittir.

Eğer dayanak köşeleri açılarının ölçüleri 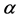ve 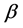ile ve diğer köşelerin açı ölçülerini ile gösterecek

olursak, olur.

Bu teoremi çokgenin dayanak köşelerinin birinden çizilen köşegenler yardımında tane üçgene ayırıp oluşan üçgenlerin açılarından faydalanabiliriz.

Şekil 7. Çokgen.

Meydana gelen tane eşitliği karşılıklı topladığımızda teoremin ispatını da tamamlamış oluruz. Eğer dış açı işaretinin eksi olarak tanımlanmasından faydalanacak olursak; Galileo geometrisinde çokgenin iç açıları toplamının sıfıra denk olduğu görülecektir. Bunu kolaylıkla bir üçgen üzerinde Şekil 8 de olduğu gibi, hatırlayarak aşağıda ki gibi ispat edebiliriz [3] .

Şekil 8. İç açılar toplamı.

.

Geometride alan ve hacim düşüncelerine de yine Afin kavramları olarak bakabiliriz. Dolayısıyla Galileo geometrisindeki alan Öklid geometrisindeki alan ile aynı olacaktır [4] .

Teorem 5.

Bir üçgenin alanı, onun tabanıyla yüksekliğinin çarpımının yarısına eşittir.

İspat: Tabanı olan ve koordinat ekseninde yerleştirilmiş üçgenine bakalım. Burada üçgenin Öklid manasındaki alanı dir.

Şekil 9. Üçgen.

Şekil 10. Üçgen.

üçgenimizi köşesinden açısı kadar döndürdükten sonra,

ve olur. Bunlardan da elde edilir. Fakat kenarı üçgeninin tabanı ve doğru parçası özel doğru üzerinde bulunmaktadır. Dolayısıyla Galileo geo- metrisinde de taban ve de yüksekliktir. Alanlar eşitliğinden teoremin doğru olduğu ortaya çıka- caktır.

Şekil 10 da gösterildiği gibi Galileo geometrisindeki hareket esnasında taban uzunluğu ve yüksekliği değişmemektedir [5] . Dolayısıyla eşitliğin herhangi bir üçgen için geçerli olduğu ortaya çıkacaktır. Şimdi bir üçgenin köşelerinden geçen yükseklikleri sırasıyla ile gösterelim ve Galileo geometrisinde açı ve yükseklik tanımlarından da faydalanarak Şekil 11’ i oluşturalım.

Şekil 11. Galileo geometrisinde üçgenin açı ve yükseklikleri.

ve eşitliklerini, ve buradan da,

ve eşitliklerini yazabiliriz.

Şekil 12 de gösterildiği gibi, Galileo geometrisinde bir üçgenin alanı iki kenar uzunluğu ve arasında kalan açının çarpımının yarısına eşit olduğu görülür. Alanı ifade eden eşitliklerden faydalanarak;

Şekil 12. Üçgen.

1. durum: buradan ve olur.

2. durum: buradan ve olur.

3. durum: buradan ve olur.

Bu üç durumdan; eşitliği yazılabilinir. Daha sonra bu eşit- lik ile sadeleştirildikten sonra eşitliğini elde edebiliriz. Bu eşitlik Öklid geo- metrisindeki Sinüs teoreminin benzeri olduğu görülür.

Galileo düzleminde herhangi bir noktası alalım. Şekil 13 de gösterildiği gibi köşegeni olan, kenarları bir birimlik mesafedeki özel doğru parçalarından oluşan paralelkenarını çizelim. Burada ve koordinatlarını belirtelim.

Şekil 13. Bir köşesi orjinde bulunan paralelkenar.

ve buradan da olur.

3. Sonuç

Sonuç olarak Galileo geometrisini, vektör normuna ait dörtgenin alanına eşit olan vektör uzayı şeklinde de öğrenebilmemiz mümkündür. İşte bu sonuçtan aşağıdaki Teoremi yazabiliriz.

Teorem 6.

Köşeleri noktalarında olan dörtgenin alanı vektörünün normuna (uzunluğuna) eşittir.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Yaglom, I.M. (1979) A Simple Non-Euclidean Geometry and Its Physical Basis. Springer-Verlag, New York.
[2]	Kurudirek, A. and Akca, H. (2015) Explanation of Distance, Kinematic and Isometry to High School Students from Different Perspective. Macrothink Institute, International Research in Education, 3.
[3]	Kurudirek, A. and Akça, H. (2015) On the Concept of Circle and Angle in Galilean Plane. Open Access Library Journal, 2, e1256. http://dx.doi.org/10.4236/oalib.1101256
[4]	Artıkbayev, A., Kurudirek, A. and Akça, H. (2013) Occurrence of Galilean Geometry. Applied and Computational Mathematics, 2, 115-117. http://dx.doi.org/10.11648/j.acm.20130205.11
[5]	Kurudirek, A., Akça, H. and Erdoğan, M. (2013) On Geometries in Affine Plane. Applied and Computational Mathematics, 2, 127-129. http://dx.doi.org/10.11648/j.acm.20130206.13