Inverse Problem for a Time-Series Valued Computer Simulator via Scalarization ()
Received 25 April 2016; accepted 25 June 2016; published 28 June 2016

1. Introduction
Experimentation with computer simulators has gained much popularity in the last two-three decades for applications where actual physical experiment is either too expensive, time consuming, or even infeasible. The applications range from drug discovery, medicine, agriculture, industrial experiments, engineering, manu- facturing, nuclear research, climatology, astronomy, green energy to business and social behavioural research. A computer simulator (or computer model), built with the help of an application area expert, is often a mathe- matical model implemented in C/C++/Java/etc. which aims to mimic the underlying true physical phenomenon. Thus, the ultimate objective of the (unobservable) experiment with the true physical process (or phenomenon) can be fulfilled via the computer simulators.
In this paper, we are interested in the inverse problem for deterministic simulators, i.e., find the input(s) of the simulator that corresponds to a pre-specified output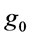 . That is, if
. That is, if 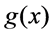 represents the simulator response for an input
represents the simulator response for an input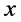 , then the objective is to find
, then the objective is to find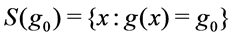 . The inverse problem is also referred to as the history matching problem or (pre-)calibration problem, contour (or iso-surface) estimation, etc. Ranjan et al. [1] proposed a sequential design framework for efficient estimation of the inverse solution when the simulator returned a scalar response, whereas the simulator under consideration in this paper gave time-series response. That is, we are interested in a functional inverse problem.
. The inverse problem is also referred to as the history matching problem or (pre-)calibration problem, contour (or iso-surface) estimation, etc. Ranjan et al. [1] proposed a sequential design framework for efficient estimation of the inverse solution when the simulator returned a scalar response, whereas the simulator under consideration in this paper gave time-series response. That is, we are interested in a functional inverse problem.
This research is motivated by two real-life applications. The first application comes from the apple farming industry in the Annapolis valley, Nova Scotia, Canada, where the objective is to find a suitable set of parameters of the two-delay blowfly (TDB) model that corresponds to the reality. TDB model simulates population growth of European red mites which infest on apple leaves and diminish the quality of crop ( [2] ). The data collection for the true population growth of these mites is very expensive, as the field expert would have to periodically count the mites on the leaves of apple trees in multiple orchards. That is, the inverse problem or equivalently, the history matching problem is to find the inputs of the TDB model that generates growth curve close to the actual data collected from a specific apple orchard in Nova Scotia, Canada.
The second application focuses on the calibration of a simulator which projects the inflation rate of a country over a period of time. Inflation or increase in overall price level is a key metric in determining the economic and financial health of a country, and the central banks are the key policy makers involved in such projections or setting up a target (http://www.imf.org/external/pubs/ft/fandd/basics/target.htm). To steer the actual inflation towards the target, the central banks control its driver, the interbank interest rate. We use a computer model called Chair-The-Fed (CTF), designed by the Federal Reserve System (referred as the Fed) of United States of America (USA), which simulates inflation rates for a given interbank interest rate over a period of time. The underlying inverse problem (also known as the pre-calibration problem) is to find out an interbank interest rate (the input of the CTF model) that leads to inflation rates closest to the target.
Though the computer models are cheaper/feasible alternatives of the unobservable/expensive physical pro- cesses, realistic simulators of complex physical phenomena can also be computationally demanding, i.e., one run may take from seconds/minutes to days/months. In such a scenario, a statistical metamodel or surrogate is often used to emulate the outputs of the simulator and draw inference based on the emulated surrogate. In computer experiment literature, Gaussian process (GP) model is perhaps the most popular class of statistical surrogate because of its flexibility, closed form predictors, and ability to incorporate various uncertainties in model specification ( [3] [4] ).
Given that the simulator is expensive (computationally or otherwise), one has to be very careful in selecting the input points while training the surrogate. One efficient method is to use a sequential design framework that exploits the overall objective. For instance, [5] developed an expected improvement (EI)-based design scheme for estimating global minimum, and in the same spirit [1] proposed another EI criterion for estimating a pre-specified contour. See [6] for a brief review. Since the simulator under consideration returns time-series response, the sequential approach with standard GP model by [1] cannot directly be used.
We propose scalarizing this functional inverse problem by first computing the Euclidean distance, 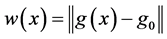 for every x and then find the global minimum of
for every x and then find the global minimum of 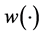 using the EI-based sequential approach with GP model proposed by [5] . Examples in Section 4 illustrates that among all realizations of GP that emulate
using the EI-based sequential approach with GP model proposed by [5] . Examples in Section 4 illustrates that among all realizations of GP that emulate , a few (in fact numerous) realizations would give negative
, a few (in fact numerous) realizations would give negative  for x near the global minimum, which is unacceptable as
for x near the global minimum, which is unacceptable as 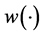 is the Euclidean distance. To alleviate this theoretical glitch, we first propose building a non-stationary surrogate of
is the Euclidean distance. To alleviate this theoretical glitch, we first propose building a non-stationary surrogate of 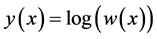 via Bayesian Additive Regression Tree (BART) model ( [7] ) and then find the global minimum of
via Bayesian Additive Regression Tree (BART) model ( [7] ) and then find the global minimum of 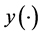 using the EI-based scheme as in [8] .
using the EI-based scheme as in [8] .
The rest of the article is organized as follows: Section 2 presents a brief review of the statistical surrogates and the sequential design scheme. Section 3 discusses the functional inverse problem, the scalarization step and the resultant scalar inverse problem. In Section 4, we present the results on the performance comparison of y-inverse and w-inverse via both test functions and two real applications: calibration of TDB model, and CTF model. Finally Section 5 concludes the paper with a few remarks.
2. Review
In this section, we briefly review the GP model, key features of BART model as a non-stationary surrogate for computer models, and the EI-based sequential design scheme for estimating the global minimum of w- and 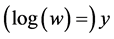 -surface. For this section, we assume that the simulator returns scalar response
-surface. For this section, we assume that the simulator returns scalar response 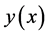 for d- dimensional input
for d- dimensional input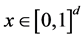 .
.
2.1. Gaussian Process Models
Sacks et al. [3] suggested using realization of a GP for emulating deterministic computer simulator outputs. Since then several variations have been proposed for building surrogates of expensive computer models (see [4] , [9] ). The simplest version of a GP model with n training points, 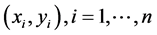 , is given by
, is given by
![]() (1)
(1)
where ![]() is the mean term and
is the mean term and ![]() is a GP with
is a GP with ![]() and spatial covariance structure defined as
and spatial covariance structure defined as
![]() , denoted by
, denoted by![]() . The most important com-
. The most important com-
ponent of the GP model, which makes it very flexible, is the correlation structure. Gaussian correlation is perhaps the most popular because of its properties like smoothness and usage in other areas like machine learning and geostatistics, whereas, both power-exponential and Matern can be thought of as generalizations of the Gaussian correlation. The power-exponential correlation is given by
![]() (2)
(2)
where ![]() are the smoothness parameters, and
are the smoothness parameters, and ![]() measures the correlation lengths. Gaussian correlation corresponds to
measures the correlation lengths. Gaussian correlation corresponds to ![]() for all
for all![]() . This model can be fitted either via the maximum likelihood estimation (MLE) or a Bayesian approach. Under the likelihood approach, the best linear unbiased predictor of
. This model can be fitted either via the maximum likelihood estimation (MLE) or a Bayesian approach. Under the likelihood approach, the best linear unbiased predictor of ![]() is
is
![]() (3)
(3)
where![]() , and the associated uncertainty
, and the associated uncertainty
(mean squared error) is
![]() (4)
(4)
It turns out that the actual implementation of both methods (MLE and Bayesian) suffer from numerical instability in computing the determinant and inverse of R. The problem of numerical instability is certainly more pronounced for GP models with Gaussian correlation as compared to other power-exponential and Matern correlation. See [10] for more details. Popular implementations of the GP model like mlegp [11] , GPfit ( [12] ), GPmfit [13] , and DiceKriging ( [14] ) use some sort of numerical fix to overcome the computational instability issue. We used GPfit in R for all implementations of the GP model.
If the process is believed to be non-stationary (e.g., ![]() in this case), one possibility is to modify the covariance parameters to capture this variation, for example,
in this case), one possibility is to modify the covariance parameters to capture this variation, for example, ![]() and
and ![]() can be a function of x. Another popular alternative is to use “treed Gaussian process” (TGP) model proposed by [15] , where the main idea is to split the input space into rectangles and fit separate GP model in each rectangle. Chipman et al. [8] found TGP somewhat unreliable and proposed the usage of a more flexible non-parametric statistical metamodel called BART (Bayesian additive regression tree).
can be a function of x. Another popular alternative is to use “treed Gaussian process” (TGP) model proposed by [15] , where the main idea is to split the input space into rectangles and fit separate GP model in each rectangle. Chipman et al. [8] found TGP somewhat unreliable and proposed the usage of a more flexible non-parametric statistical metamodel called BART (Bayesian additive regression tree).
2.2. BART Model
Chipman et al. [7] proposed BART for approximating the conditional mean of the response given the data using a sum of regression trees. In our context, the computer simulator output can be emulated using the BART model as
![]() (5)
(5)
where![]() . This model assumes the existence of m binary trees
. This model assumes the existence of m binary trees ![]() (
(![]() ) each containing a set of interior node decision rules and b terminal nodes. The parameter
) each containing a set of interior node decision rules and b terminal nodes. The parameter ![]() represents the set of mean response parameters at each terminal node of
represents the set of mean response parameters at each terminal node of![]() . The predicted outcomes of the computer simu- lator are obtained by sequentially following the decision rules for each tree
. The predicted outcomes of the computer simu- lator are obtained by sequentially following the decision rules for each tree ![]() until reaching a terminal node, and then summing up these terminal node values (i.e.,
until reaching a terminal node, and then summing up these terminal node values (i.e., ![]() , for
, for![]() ,
,![]() ). Thus, viewed as a function of x, tree model
). Thus, viewed as a function of x, tree model ![]() produces a piecewise-constant output.
produces a piecewise-constant output.
The “ensemble” of m such tree models in (5) makes the BART model very flexible. It is capable of incor- porating higher-dimensional interactions, by adaptively choosing the structure and individual rules of the Tj’s. Furthermore, many individual trees ![]() may place split points in the same area, allowing the predicted function to change rapidly nearby, effectively capturing non-stationary behaviour such as abrupt changes in the response.
may place split points in the same area, allowing the predicted function to change rapidly nearby, effectively capturing non-stationary behaviour such as abrupt changes in the response.
The model fitting is done via a Markov Chain Monte Carlo (MCMC) Bayesian backfitting algorithm. Each
iteration of the this algorithm generates one draw from the posterior distribution of![]() . Let
. Let
![]() denote N draws of the posterior of
denote N draws of the posterior of![]() . Given a reasonable burn-in period B and thinning constant
. Given a reasonable burn-in period B and thinning constant![]() , estimates of the computer simulator can be obtained as simply the average of the observed posterior draws, i.e.,
, estimates of the computer simulator can be obtained as simply the average of the observed posterior draws, i.e.,
![]() (6)
(6)
where![]() . Estimates of the predicted variation can similarly be computed as the 5th and 95th quantiles or standard deviation of observed posterior draws. We follow the same formulation of prior as in [7] , i.e., 1)
. Estimates of the predicted variation can similarly be computed as the 5th and 95th quantiles or standard deviation of observed posterior draws. We follow the same formulation of prior as in [7] , i.e., 1) ![]() are i.i.d.; 2) all elements of
are i.i.d.; 2) all elements of ![]() are i.i.d. given all T’s, and
are i.i.d. given all T’s, and ![]() is independent of all T's and M’s.
is independent of all T's and M’s.
For applying BART to our deterministic computer experiment, we relax the default prior, ![]() with
with![]() , to
, to![]() . Choosing a smaller value of k increases the prior variance of output applying less shrinkage (or smoothness) of the response. The deterministic assumption also requires modification to the prior on
. Choosing a smaller value of k increases the prior variance of output applying less shrinkage (or smoothness) of the response. The deterministic assumption also requires modification to the prior on![]() . This is accomplished with the same inverted-chi-squared prior for
. This is accomplished with the same inverted-chi-squared prior for ![]() as in [7] , using their recommended value of 3 degrees of freedom, and anchoring the 90th percentile of the
as in [7] , using their recommended value of 3 degrees of freedom, and anchoring the 90th percentile of the ![]() prior at 0.20 × sd(y), where sd(y) is the sample standard deviation of the training y values. This strategy facilitates MCMC mixing for BART, and can also be considered as having a nugget in GPs, for numeric stability and predictive accuracy.
prior at 0.20 × sd(y), where sd(y) is the sample standard deviation of the training y values. This strategy facilitates MCMC mixing for BART, and can also be considered as having a nugget in GPs, for numeric stability and predictive accuracy.
In this paper we use the freely available R package BayesTree for implementing all BART models. Recently, [16] have developed a computationally more efficient surrogate model equipped with parallel computing func- tionality.
2.3. Sequential Design
Given the fixed budget of n simulator evaluations, a naive method of estimating a pre-specified feature of interest (FOI) would be to first choose n input (training) points in a space-filling manner, build (train) the surrogate, and then estimate the FOI from this fitted emulator. Popular space-filling designs in computer experiment applications are Latin hypercube designs (LHDs) with space-filling properties like maximin, mini- mum pairwise coordinate correlation, orthogonal arrays, etc.
It has been shown via numerous illustrations in the literature that any reasonably designed sequential sampling scheme outperforms the naive one-shot design approach. The key steps of a sequential design framework is summarized as follows:
1) Choose an initial set of points ![]() from the input space
from the input space![]() .
.
2) Obtain the vector of corresponding simulator outputs![]() .
.
3) Fit a statistical surrogate using the data D and response vector![]() .
.
4) Estimate the feature of interest (FOI) from the trained (fitted) surrogate.
5) If (the budget is exhausted, or a stopping criterion has met), then exit, else continue.
6) a) Find a new input point (or set of points) ![]() by optimizing a merit-based criterion (e.g., EI criterion).
by optimizing a merit-based criterion (e.g., EI criterion).
b) Obtain ![]() from the computer simulator.
from the computer simulator.
c) Append ![]() and
and ![]() to the current design and computer simulator response, respectively, forming
to the current design and computer simulator response, respectively, forming ![]() and
and![]() .
.
7) Go back to Step 3 (refit the surrogate with the updated data).
For the surrogate in Step 3, we consider both the GP model and BART, and the FOI is the global minimum. The most important part of this sequential framework is Step 6(a). Though one can easily come up with a merit- based criterion, proposing a good one, that can lead to the global minimum in the fewest number of follow-up runs, is not easy.
Jones et al. [5] proposed the most popular sequential design criterion in computer experiment literature called the expected improvement (EI) with the objective of finding the global minimum of an expensive deterministic com- puter simulator. The proposed improvement at an untried point ![]() is given by
is given by![]() ,
,
where ![]() is the current best estimate of the global minimum, and
is the current best estimate of the global minimum, and![]() . Then, EI is simply
. Then, EI is simply
the expected value of ![]() with respect to the predictive distribution. That is,
with respect to the predictive distribution. That is,
![]() (7)
(7)
where ![]() and
and ![]() are the standard normal probability density function and cumulative distribution functions, respectively. Finally, the new point to be added to the experimental design is chosen as the point with the largest measured EI value, that is
are the standard normal probability density function and cumulative distribution functions, respectively. Finally, the new point to be added to the experimental design is chosen as the point with the largest measured EI value, that is
![]() (8)
(8)
Inspired by [5] , a host of EI criteria have been proposed for estimating different FOIs. See [6] for a recent review on such merit-based design criteria. Finding the optimal follow-up design point also depends on the accuracy of EI optimization. It turns out that the EI surfaces are typically multi-modal, and the location and number of prominent modes/peaks changes from iteration-to-iteration. Popular optimization techniques used for EI optimization include, genetic algorithm ( [1] ), particle swarm optimization [13] , multistart newton-based methods ( [12] ), and branch-and-bound algorithms [17] . Thus, one should be careful in choosing the follow-up points to achieve the optimal improvement at every step.
3. Inverse Problem for Time-Series Response
In this paper, we assume that the computer simulator is deterministic, takes a d-dimensional input ![]() and returns a time-series response
and returns a time-series response![]() . Our main objective is find
. Our main objective is find ![]() such that
such that ![]() for all
for all![]() , where
, where ![]() is a pre-specified process output (e.g., the true observed field data in the TDB model application, or the target inflation rates in the CTF model application). This inverse problem with time-series/functional response is also refereed to as the calibration problem, wherein, the main objective is to calibrate the computer model at a certain
is a pre-specified process output (e.g., the true observed field data in the TDB model application, or the target inflation rates in the CTF model application). This inverse problem with time-series/functional response is also refereed to as the calibration problem, wherein, the main objective is to calibrate the computer model at a certain ![]() so that the computer simulator produces desirable (realistic/close to target) response.
so that the computer simulator produces desirable (realistic/close to target) response.
The key idea is to propose a scalarization strategy that transforms the functional inverse problem to a minimization problem for a scalar-valued simulator. That is, for every![]() , first transform the simulator output
, first transform the simulator output ![]() to
to ![]() as follows:
as follows:
![]()
then find the global minimum of![]() . We use EI-based sequential design scheme with GP model as a surrogate (by [5] ) to efficiently minimize
. We use EI-based sequential design scheme with GP model as a surrogate (by [5] ) to efficiently minimize![]() .
.
It is important to note that the predicted realizations of ![]() under the GP model will not always be positive. For instance, the prediction near the global minimum has a good chance of being negative (see Figure 2(b) in Section 4). This may not be critical from the inverse problem’s viewpoint, as the negative values of
under the GP model will not always be positive. For instance, the prediction near the global minimum has a good chance of being negative (see Figure 2(b) in Section 4). This may not be critical from the inverse problem’s viewpoint, as the negative values of ![]() near the global minimum in some iterations of the sequential design scheme do not hinder the efficiency in finding the location of the global minimum, i.e., the inverse solution for
near the global minimum in some iterations of the sequential design scheme do not hinder the efficiency in finding the location of the global minimum, i.e., the inverse solution for![]() . However, a negative value of
. However, a negative value of ![]() has no real/feasible inverse mapping to
has no real/feasible inverse mapping to![]() .
.
One possibility is to fit a log-GP model, i.e., fit a GP model to![]() . However, as shown in Figure 3(c) and Figure 6(c)
. However, as shown in Figure 3(c) and Figure 6(c) ![]() is often non-stationary near the global minima, and a standard GP would not be suitable for this either. We use a flexible surrogate called BART model [7] for emulating
is often non-stationary near the global minima, and a standard GP would not be suitable for this either. We use a flexible surrogate called BART model [7] for emulating![]() . Subsequently, we use the EI-based sequential design scheme with the BART-based surrogate for efficient minimization of the scalarized response
. Subsequently, we use the EI-based sequential design scheme with the BART-based surrogate for efficient minimization of the scalarized response ![]() (e.g., in [8] ).
(e.g., in [8] ).
Next we use simulated and real-life examples to compare the performance of the EI-BART method for minimizing ![]() with the naive EI-GP method for minimizing
with the naive EI-GP method for minimizing![]() .
.
4. Results
In this section, we consider the functional inverse problems for one test function with slight variations that enables 1-, 2- and 3-(dimensional) inputs, TDB model with six-dimensional inputs, and CTF model with 1-dimensional input. For all examples, we use both EI-BART and EI-GP approaches with the same sequential settings, i.e., same ![]() (initial design size) +
(initial design size) + ![]() (follow-up points). In fact, the initial design points are same for both methods. Moreover, we keep the GP and BART settings same for all examples.
(follow-up points). In fact, the initial design points are same for both methods. Moreover, we keep the GP and BART settings same for all examples.
Example 1. Suppose the simulator ![]() takes an input
takes an input ![]() and generates a time-series response with
and generates a time-series response with![]() , as per the following model:
, as per the following model:
![]() (9)
(9)
Let the true field data correspond to![]() . Figure 1 shows the true field data (solid red curve) and the computer model outputs for a few randomly generated inputs
. Figure 1 shows the true field data (solid red curve) and the computer model outputs for a few randomly generated inputs ![]() (shown in blue dotted curves). Here, the inverse problem simplifies to finding the input of the simulator
(shown in blue dotted curves). Here, the inverse problem simplifies to finding the input of the simulator ![]() such that the corresponding dashed blue curve overlays completely on the solid red curve.
such that the corresponding dashed blue curve overlays completely on the solid red curve.
Figure 2 illustrates results for EI-GP implementation with ![]() and
and![]() . The estimated
. The estimated ![]() is 0.5000 and the corresponding minimum
is 0.5000 and the corresponding minimum ![]() is 0.0004.
is 0.0004.
It is clear from Figure 2(d) that the global minimum was located very quickly in this sequential procedure, which was expected given the simplicity of the test function. Figure 2(b) also shows that many realizations of the GP model that emulate the training data would give negative value of ![]() in the vicinity of the global minimum (the confidence band shown in red dashed curves around the blue solid curve goes below zero in the interval
in the vicinity of the global minimum (the confidence band shown in red dashed curves around the blue solid curve goes below zero in the interval![]() ).
).
Figure 3 shows EI-BART illustration with the same sequential settings as in Figure 2 for finding the minimum of![]() . The estimated
. The estimated ![]() is 0.4999 and the value of the corresponding minimum
is 0.4999 and the value of the corresponding minimum ![]() is
is ![]() (with
(with![]() ).
).
Both EI-BART and EI-GP find the global minimum, but EI-GP exhibit much faster convergence. This is also expected as BART is typically a bit more data-hungry than the GP models. Further note from Figure 3(c) that ![]() surface is highly non-stationary near the global minimum.
surface is highly non-stationary near the global minimum.
![]()
Figure 1. A few computer model outputs and the true field data for Example 1.
![]()
Figure 2. Sequential optimization of ![]() via the GP-based emulator for Example 1.
via the GP-based emulator for Example 1.
Example 2. Consider the same test function as in Example 1, with a small modification that would allow two-dimensional inputs ![]() and generates time-series response in the same time domain. That is,
and generates time-series response in the same time domain. That is,
![]() (10)
(10)
Let the true field data correspond to![]() . Figure 4 shows the true field data (solid red curve) and a few simulator outputs (blue dotted curves).
. Figure 4 shows the true field data (solid red curve) and a few simulator outputs (blue dotted curves).
For this inverse problem, we used ![]() initial design points and
initial design points and ![]() follow-up points as per the EI criterion. Figure 5 shows the illustration of the EI-GP approach. The estimated
follow-up points as per the EI criterion. Figure 5 shows the illustration of the EI-GP approach. The estimated ![]() is
is ![]() and the corresponding minimum
and the corresponding minimum ![]() is 0.0344.
is 0.0344.
Figure 5(d) shows that a decent value of the global minimum has been found after 9 - 10 follow-up trials. Of course, the efficiency can perhaps be improved by exploring different ![]() and
and ![]() combination. As expected
combination. As expected
![]()
Figure 3. Sequential optimization of ![]() via BART-based emulator for Example 1.
via BART-based emulator for Example 1.
EI-BART requires a few more points to attain the same accuracy level (see Figure 6). The estimated ![]() is
is ![]() and the corresponding minimum
and the corresponding minimum ![]() is
is ![]() (i.e.,
(i.e.,![]() ).
).
Example 3. Again we consider the same base example (as in Example 1) with a slight twist to the simulator to allow a three-dimensional input![]() , i.e.,
, i.e.,
![]() (11)
(11)
Furthermore, we assume that the true field data correspond to![]() . Figure 7 shows the true field data (solid red curve) and a few simulator outputs (blue dotted curves). This inverse problem appears to be a little more challenging than the previous ones.
. Figure 7 shows the true field data (solid red curve) and a few simulator outputs (blue dotted curves). This inverse problem appears to be a little more challenging than the previous ones.
As the input dimension grows, we have increased the initial design size and the overall budget to ![]() and
and ![]() respectively. Figure 8 compares the performance of EI-GP and EI-BART. As expected EI-GP is
respectively. Figure 8 compares the performance of EI-GP and EI-BART. As expected EI-GP is
![]()
Figure 4. A few model outputs and the true field data for the simulator in Example 2.
![]()
Figure 5. Sequential optimization of ![]() via the GP-based emulator for Example 2.
via the GP-based emulator for Example 2.
![]()
Figure 6. Sequential optimization of ![]() via the BART-based emulator for Example 2.
via the BART-based emulator for Example 2.
leading by a small margin, but EI-BART is a theoretically more correct methodology to follow.
Under EI-GP, the final estimate of ![]() is
is ![]() and the corresponding estimate of the global minimum of
and the corresponding estimate of the global minimum of ![]() is 0.1259, whereas for EI-BART, the estimated
is 0.1259, whereas for EI-BART, the estimated ![]() is
is ![]() and the estimated global minimum
and the estimated global minimum ![]() is 0.3913. Though the final inverse solution (x-values) and the estimated global minimum appear to be slightly different for the two methods, the simulator responses at the two inverse solution are almost indistinguishable (Figure 9).
is 0.3913. Though the final inverse solution (x-values) and the estimated global minimum appear to be slightly different for the two methods, the simulator responses at the two inverse solution are almost indistinguishable (Figure 9).
Example 4. Annapolis Valley in Nova Scotia, Canada is popular for its apple farming. Unfortunately, apple orchards are susceptible to the infestation of pests. Of particular interest is the Panonychus ulmi (Koch) or European red mite (ERM).
Growth cycle of a mite consists of three stages (1) egg (2) juvenile and (3) adult. These mites start their lives
![]()
Figure 7. A few computer model outputs and the true data for Example 3.
![]()
Figure 8. Running estimate of ![]() obtained under the two methods of finding inverse solution for Example 3.
obtained under the two methods of finding inverse solution for Example 3.
as eggs that are laid in the late summer months of the previous year. Once the temperature rises to a sufficient level the following spring, these eggs hatch and emerge as larvae which further grow to juveniles followed by egg-laying adults. During the summer, adult female ERM lay eggs that hatch during the same season due to the warmer climate. Finally, in mid-to-late August, ERM lay eggs and the cycle repeats itself.
For deeper understanding of the dynamics of ERM population growth, data collection and analysis is important, but the field data collection from apple orchards is very expensive, as the field experts would have to physically go to the orchard on multiple occasions and count the number of mites (in different stages) from the leves of trees. Tiesmann et al. (2009) proposed a two-delay blowfly (TDB) model that tries to mimic the population growth of these mites. Figure 10 presents a few TDB models output along with the corresponding field data collected with significant effort for the juvenile group.
Though there are several parameters of this TDB model, the following six parameters turned out to be very
![]() (a) EI-GP
(a) EI-GP![]() b) EI-BART
b) EI-BART
Figure 9. Comparison of the best solution found under EI-GP and EI-BART for Example 3.
influential:
・ ![]() ―adult death rate;
―adult death rate;
・ ![]() ―maximum fecundity (eggs laid per day);
―maximum fecundity (eggs laid per day);
・ ![]() ―non-linear crowding parameter;
―non-linear crowding parameter;
・ ![]() ―(first delay) hatching time of summer eggs;
―(first delay) hatching time of summer eggs;
・ ![]() ―(second delay) time to maturation of recently hatched eggs;
―(second delay) time to maturation of recently hatched eggs;
・ Season―average number of days on which adults switch to laying winter eggs.
The TDB model returns the population growth of all three stages of mite, we focus only on the growth cycle of “juveniles” in this paper. A feasible range of x was elicited by the experts for running the TDB model. The main objective of this study is to use the proposed sequential strategy to efficiently calibrate the TDB model so that it returns realistic outputs. That is, find x (six-dimensional) such that ![]() matches (or approximates) the reality.
matches (or approximates) the reality.
As in the earlier examples, we apply both EI-BART and EI-GP with ![]() and
and ![]() to find the desired inverse solution. Figure 11 shows the running estimate of the global minimum of
to find the desired inverse solution. Figure 11 shows the running estimate of the global minimum of![]() .
.
![]()
Figure 10. A few realisation of juvenile growth curves from the TDB model, and the true average field data collected from the Annapolis valley, NS, Canada.
![]()
Figure 11. Running estimate of ![]() obtained under the two methods of finding inverse solution for TDB simulator.
obtained under the two methods of finding inverse solution for TDB simulator.
From Figure 11 it is clear than EI-GP outperforms EI-BART. (![]() and 40.72 for EI-BART and EI-GP respectively). Moreover, the best TDB model match obtained via the two methods (Figure 12) show that either additional follow-up points or a different (
and 40.72 for EI-BART and EI-GP respectively). Moreover, the best TDB model match obtained via the two methods (Figure 12) show that either additional follow-up points or a different (![]() ) combination may be required to achieve higher accuracy.
) combination may be required to achieve higher accuracy.
Example 5. Inflation and unemployment are two key tools to measure the financial health of a country. Typically central bank of a country, like the Federal Reserve System (referred to as the Fed) in the United States of America (USA), is mandated to minimize unemployment rate and stabilize prices of goods and services. Central banks aim to do so by controlling the interbank borrowing rate, i.e. the rate of interest at which banks and credit institutions can raise fund overnight from other similar institutions. Decision on interest rate is thus a
![]()
Figure 12. Best TDB model runs obtained via the two sequential procedure.
crucial component of monitory policy for a country.
The monetary policy making body of the Fed, Federal Open Market Committee (FOMC), announces pro- jected inflation (measured using personal consumption expenditures) and unemployment rates based on the analysis of its members for the current year as well as next two years. In this paper, we focus on the inflation rates. Figure 13 presents the projected inflation rate from the January meeting announcements of FOMC for each year during 2006-2015 (see https://www.federalreserve.gov/monetarypolicy/fomccalendars.htm and https://www.federalreserve.gov/monetarypolicy/fomc_historical.htm).
Several interesting theories and models have been proposed thus far to understand the rates projected by the Fed (e.g., [18] [19] ). We focus on the simulator called Chair-the-Fed (CTF)
(http://sffed-education.org/chairthefed/WebGamePlay.html), wherein one can select the interbank borrowing rate (i.e., funds rate, the input-x) and observe the simulated inflation rates for the next 10 time points (years). The CTF model allows x to vary between 0 and 20 with an increment of 0.25. Figure 13 depicts a few simulated model runs overlay with the projected rates. Assuming that the Fed funds rate remains static for the next 10 time points, one can play the game (i.e., run the CTF model) and generate a set of inflation fund rates. Our main objective is to find the fund rate (x) which generates the inflation rates curve closest to the target (projected values) set by FOMC.
Since the CTF simulator is only one-dimensional, we started the sequential approach in both EI-GP and EI- BART with only ![]() initial points, however, added upto 35 follow-up points to ensure the global minimum. The results from the sequential search of the inverse solution are displayed in Figure 14 and Figure 15. Both sequential approaches led to the same inverse solution. As shown in Figure 14, EI-BART converged to the global
initial points, however, added upto 35 follow-up points to ensure the global minimum. The results from the sequential search of the inverse solution are displayed in Figure 14 and Figure 15. Both sequential approaches led to the same inverse solution. As shown in Figure 14, EI-BART converged to the global
![]()
Figure 13. A few realisation of the inflation rates curve from the CTF model (blue dashed curves), and the true projected rates set by the Fed and FOMC (red solid curve).
![]()
Figure 14. Running estimate of ![]() obtained under the two methods of finding inverse solution for CTF simulator.
obtained under the two methods of finding inverse solution for CTF simulator.
![]()
Figure 15. Best Chair-The-Fed (CTF) model runs obtained via the two se- quential procedure (EI-GP and EI-BART). The solid (red) curve denotes the truth (target inflation rates curve) and the dashed (blue) curve represents the best match found by the CTF model.
minimum with relatively fewer additional model evaluations as compared to the number points needed by EI-GP.
The discrepancy in the target inflation rates curve and the best match produced by CTF model is perhaps attributed to the discreteness in the x-space (CTF allows inputs in the interval (0.20) with a jump of 0.25), or the fact that x is not allowed to vary with time, or perhaps additional input variables have to be included to get a closer match. Furthermore, higher efficiency can perhaps be achieved by exploring the right ![]() combination.
combination.
5. Concluding Remarks
In this paper, we focused on an inverse problem for deterministic computer simulator with time-series (or functional) outputs. Our main focus was on reducing the complexity of the problem from time-series response to scalar by scalarization, ![]() , where
, where ![]() and
and ![]() were the target (pre-specified) and simu- lator (time-series) response, respectively. We were also interested in solving the inverse problem with as few simulator runs as possible. This is particularly useful if the simulator is expensive to evaluate, and/or if the input dimension is large which prohibits thorough exploration of the input space.
were the target (pre-specified) and simu- lator (time-series) response, respectively. We were also interested in solving the inverse problem with as few simulator runs as possible. This is particularly useful if the simulator is expensive to evaluate, and/or if the input dimension is large which prohibits thorough exploration of the input space.
The efficiency (minimizing the number of simulator runs) is achieved by using EI-based sequential design scheme and surrogate-based approach. It is explained in Section 3 that the most popular choice of surrogate in computer experiment (GP model) is theoretically inappropriate, however, as illustrated through multiple ex- amples, EI-GP approach works equally well for finding the inverse solution. Even if we ignore this theoretical glitch, there is no clear winner between EI-GP and EI-BART.
There are several interesting issues that should be investigated further and we wish to work on it in our future research endeavours. A few of them are listed as follows: 1) A more thorough comparison between the two methods (EI-GP and EI-BART) should be conducted. For instance, we should use a variety of test functions, repeat the simulations to average out the effect of initial design choice, find optimal (![]() ) combination in the sequential procedure, and so on; 2) The scalarization process should be further strengthened by using more informative discrepancy measure as compared to Euclidean distance; 3) Does this scalarization procedure affect the likeliness of finding the inverse solution? That is, can this scalarization approach be used for every inverse problem with functional/time-series outputs without risking the accuracy and efficiency? A thorough com- parison with non-scalarization based methods should be conducted; 4) Is it straightforward to view the percentile estimation as a generalization of the inverse problem in this setup as well?
) combination in the sequential procedure, and so on; 2) The scalarization process should be further strengthened by using more informative discrepancy measure as compared to Euclidean distance; 3) Does this scalarization procedure affect the likeliness of finding the inverse solution? That is, can this scalarization approach be used for every inverse problem with functional/time-series outputs without risking the accuracy and efficiency? A thorough com- parison with non-scalarization based methods should be conducted; 4) Is it straightforward to view the percentile estimation as a generalization of the inverse problem in this setup as well?
Acknowledgements
Preliminary work was done by Corey Hodder during his BSc honours thesis at Acadia University, NS, Canada. Thanks to the Acadia Centre for Mathematical Modeling and Computation (ACMMaC) facility for providing access to clusters for conducting simulations. The authors also thank the reviewers for their comments.