Incessant Allocation Method for Solving Transportation Problems ()
Received 3 April 2016; accepted 28 May 2016; published 31 May 2016
1. Introduction
Transportation Problem (TP) is one of the subclasses of Linear Programming Problems in which the objective is to transport various quantities of a single homogeneous commodity that are initially stored at various origins to different destinations in such a way that the total transportation cost is minimum. To achieve this objective we must know the amount and location of available supplies and the quantities demanded. In addition, we also know the unit transportation cost of the commodity to be transported from various origins to various destinations. Few examples of TP are summarized in Table 1 [1] .
![]()
Table 1. Examples of transportation problem.
Balanced transportation problems and unbalanced transportation problems are the types of TPs. If the sum of the supplies of all the sources is equal to the sum of the demands of all the destinations, the problem is termed as a balanced TP. On the other hand, the problem is termed as unbalanced TP. The basic steps for obtaining an optimum solution to a TP are:
・ Step 1: Mathematical formulation of the TP.
・ Step 2: Verify the TP: either it is balanced or unbalanced. If the problem is unbalanced, first balance it.
・ Step 3: Determine the Initial Basic Feasible Solution (IBFS).
・ Step 4: Verify the optimality condition of the IBFS. If the solution is not optimal, improve it for obtaining optimal solution.
The basic TP was first developed by Hitchcock [2] and then the systematic solution procedures from the simplex algorithm were further developed, primarily by Dantzig [3] and then by Charnes et al. [4] . In the solution procedure of TP, IBFS is known as the fundamental stage for finding an optimal solution. The well recognized classical methods, for finding an IBFS for the transportation problems are North West Corner Rule (NWCR) [5] [6] , Least Cost Method (LCM) [5] [6] and Vogel’s Approximation Method (VAM) [5] - [7] . Again researchers worked and are working on transportation problem to develop new algorithm to find a better IBFS for TPs [8] - [34] , and these methods may be used to solve maximization transportation problems [35] - [38] and also time minimization transportation problems [29] [39] - [41] . Like other researchers, in this paper an effective procedure for finding an IBFS for the cost minimizing TPs is proposed, and the proposed method is also used to solve profit maximization TP. Exceptionality and applicability of the method are also studied and explained in this study.
2. Tabular Form of Transportation Model
The tabular form of a TP is a matrix within a matrix shown in Table 2. Cost matrix is one of them that representing unit transportation cost cij, indicating the cost of shipping one unit from the i-th origin to the j-th destination. Super impose of this matrix is the matrix of transportation variable xij, indicating the amount shipped from i-th source to j-th destination. Right and bottom sides of the transportation table point out the amounts of supplies ai available at source i and the amount demanded bj at destination j.
3. Mathematical Formulation of Transportation Problem
The TP can be stated as an allocation problem in which there are m sources (suppliers) and n destinations (customers). Each of the m sources can allocate to any of the n destinations at a per unit carrying cost cij (unit transportation cost from source i to destination j). Each sources has a supply of ai units, 
and each destination has a demand of bj units,
. The objective is to determine which routes are to be selected and the size of the shipment on those routes, so that the total transportation cost of meeting demand, given the supply constraints, is minimized. Hence the mathematical formulation of cost minimization TP is,
Minimize: 
Subject to: 
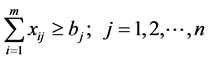
, for all i and j.
![]()
Table 2. Tabular form of transportation problem.
4. Illustration of the Proposed Method
In this research, allocations (from the first allocation to last allocation) in the cost cells are distributed in a continuous way, and for following this process, proposed method is named as “Incessant Allocation Method (IAM)” for Solving TP. Logical development of the proposed process for solving cost minimizing TP is illustrated below:
・ Step 1: Formulate the TP. For unbalanced problem, we do not require to balance the transportation problem.
・ Step 2: Find the smallest cost cell cij in the transportation table to make the first allocation. Allocate xij = min (ai, bj) in the cell (i, j). In case of ties, select the cell where maximum allocation can be allocated. Again in case of same cost cells and allocation select the cell for which sum of demand and supply is maximum in the original transportation table. Finally if all these are same, select the cell randomly.
・ Step 3: Adjust the supply and demand requirements in the respective rows and columns. Then following cases arise:
Case-1: If the allocation xij = ai, i-th row is to be crossed out and bj is reduced to (bj - ai). Now complete the allocation along j-th column by making the allocation/allocations in the smallest cost cell/cells continuously. Consider that, j-th column is exhausted for the allocation xkj in the cell (k, j). Now, follow the same procedure to complete the allocation along k-th row and continue this process until entire rows and columns are exhausted.
Case-2: If the allocation xij = bj, j-th column is to be crossed out and ai is reduced to (ai - bj). Now by following the same procedure explained in case-1, complete the allocation along i-th row and continue the process until entire rows and columns are exhausted.
Case-3: If the allocation xij = ai = bj, find the next smallest cost cell, (i, k) from the rest of the cost cells along i-th row and j-th column. Assign a zero in the cell (i, k) and cross out i-th row and j-th column. After that complete the allocation along k-th column following the process described in Case-1 to complete the allocations.
Case-4: For any allocation, other than first allocation made along the row/column satisfies both the row and column. In such case find the smallest cost cell which is along the column/row and assign a zero in that cell and continue the process described in above cases to complete the allocation along the column/row and also to complete entire allocations.
・ Step-4: Finally calculate the total transportation cost which is the sum of the product of cost and corresponding allocated value.
5. Procedure for Solving Maximization Problem
There are some TPs where the objective is to maximize the profit rather than minimizing transportation cost is known as profit maximization TP. In the solution procedure of profit maximization TP, for finding an IBFS, allocations are to be made in highest profit cells, rather than in lowest cost cells. In this research proposed method has also been applied to solve the profit maximization TP.
6. Numerical Problems
In this research 15 problems are solved randomly from various literature and books only to analyze the perfectness and to justify the usefulness of the method. These problems and their IBFS obtained by IAM, are listed in the Tables 3-5 respectively.
![]()
Table 3. Cost minimization transportation problems (balanced problems).
![]()
Table 4. Cost minimization transportation problems (unbalanced problems).
![]()
Table 5. Profit maximization transportation problems.
6.1. Solution of a Problem with Illustration
Illustrative solution makes the theorem understandable to the readers. Considering this only the solution of BTP-4 from cost minimization TPs is illustrated, mathematical formulation of this problem is shown in Table 6.
Allocation of various cells of the above problem is shown in Table 7 and this is the IBFS for the problem:
![]()
Table 7. Initial basic feasible solution of BTP-4.
・ First Allocation: Allocate 60 = min (60, 95) in the cell (6, 5) which is the smallest cost cell among all the cost cells of BTP-4. Cross out the 6-th row as this allocation satisfies this row and along 5-th column, the demand is reduced to 35 = (95 - 60).
・ Second Allocation: Now the smallest cost cell along 5-th column is 2 appears in the cell (5, 5) and allocate the reduced demand 35 in this cell. In this case 5-th column is exhausted and the supply along 5-th row is reduced to 65 = (100 - 35).
・ By following the same procedure Third Allocation is 65 in the cell (5, 3). Fourth Allocation is 75 in the cell (2, 3). Fifth Allocation is 5 in the cell (2, 4). Sixth Allocation is 35 in the cell (4, 4). Seventh Allocation is 55 in the cell (4, 2), Eighth Allocation is 30 in the cell (1, 2). Ninth Allocation is 65 in the cell (1, 6). Tenth allocation is 25 in the cell (1, 1) and the final allocation is 50 in the cell (3, 1) are made.
・ Finally total transportation cost is,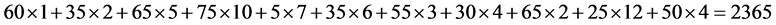 
7. Exceptionality of Proposed Method
This research finds two exceptionalities which are as follows:
・ This method does not require balancing an unbalanced transportation problem for finding an initial solution.
・ This method always yields an initial basic feasible solution for the balanced transportation problems.
7.1. Explanation of the Second Exceptionality
In the balanced TP, for an allocation either a single row or a single column is exhausted except the final allocation. If both of the row and column are exhausted for a single allocation, one zero is assigned to make the number of allocations equal to the number of row and column. Only the final allocation exhausted both the row and column together. Now for m × n transportation matrix the number of allocating cells are to be [(m + n − 2) + 1] = (m + n − 1). According to the definition of IBFS, this ensures the starting/initial solution is a basic feasible solution for the balanced TPs.
8. Result and Analysis
In this research, classical TP methods for finding an IBFS are studied in details. Hamdy A. Taha’s TORA software is used in order to find the IBFS for the methods (NWCR, LCM and VAM) and to find the optimal result. Again the initial result for the IAM is calculated manually. Finally various mathematical comparisons between the results obtained by existing methods, and IAM are shown in the Tables 8-11.
![]()
Table 8. Cost minimization transportation problems (balanced problems).
![]()
Table 9. Cost minimization transportation problems (unbalanced problems).
![]()
Table 10. Profit maximization transportation problems.
![]()
Table 11. Comparison of average of PoCIR and grand average of PoCIR.
In the comparisons mainly the initial result obtained by various methods are shown. The percentage of correctness is calculated by using the formula [% of correctness = 100 − {(initial result − optimal result) * 100/optimal result)}] for cost minimization TPs. Again, for the profit maximization transportation problems this percentage is obtained by the formula [% of correctness = 100 − {(optimal result − initial result) * 100/optimal result}]. This result is studied only to evaluate the obtained IBFS is numerically either equal to optimal result or nearer to optimal result. During this process it is observed that in most of the cases IBFS obtained by IAM is numerically optimal or nearer to optimal value.
Again average of PoCIR for each types of cost minimizing TP (balanced, unbalanced) and profit maximization TP is also studied to analyze the performance of IAM for finding IBFS. For each type of problems, it is found that this percentage for IAM is remarkably better than NWCR and LCM and parallel to the percentage obtained by VAM.
We also calculate GAPoCIR to justify the general performance of the method, which is shown in Figure 1. This figure ensures the feasibility of IAM for solving any types of TP.
Finally we acknowledge that, VAM as well as IAM yields a better IBFS for the TPs. Again computational procedure of IAM is easier than VAM. Hence from this discussion IAM can be claim an effective process for finding an IBFS.
9. Conclusion
The aim of any industry is to transport goods from sources to destinations with minimum cost. Minimization of transportation cost is one of the main objectives to maximize the profit. In this article, we propose an efficient procedure for finding an IBFS for minimizing transportation cost. Methodical evaluation of the proposed method is also carried out for both the balanced and unbalanced TPs. We also use this method in solving profit maximization TPs to justify its applicability in all types of TPs. It is also observed that our method is usually resulting in minimal and maximal values respectively for cost minimizing TPs and profit maximization TPs. Finally the proposed method presented in this paper claims its wide application in solving TPs.