1. Introduction
How to make further efforts to efficiently utilize the finite radio spectrum resources is one of the most important topics in the area of wireless communications all the time. With each passing day, more people are subscribing to one of the plethora of wireless services currently available on the market. As a result of this rapid growth in the wireless services industry, the demand for additional bandwidth is steadily increasing despite the fact that frequency spectrum is a finite natural resource [1] [2]. It is urgent to exploit and utilize the finite natural spectrum resource effectively in order to accommodate rapid growth.
Frequency division multiplexing (FDM) and time division multiplexing (TDM) can contribute to the improvement of the utilization of spectrum resources. However, the guard interval existing in FDM and TDM leads to the loss of multiplexing, which reduces the channel capacity [3] [4]. Since code division multiplexing (CDM) use orthogonal codes, there is a hard limit on how many orthogonal codes can be obtained. Non-or- thogonal codes cause mutual interference between users. Thus, the more users that simultaneously share the system bandwidth using non-orthogonal codes, the higher the level of interference, which degrades the performance of the whole system [5] [6]. Hence, the TDM, FDM and CDM schemes are limited in time interval, or frequency band or code.
A flexible and high spectrum efficient multiplexing scheme, WSDM, can transmit multiple signals simultaneously in the same frequency band over wireless channel [7] [8]. WSDM recovers the source signals at the multiple-antenna receiver by utilizing the statistical characteristics of source signals, as shown in Figure 1. Therefore, WSDM can raise frequency bandwidth efficiency greatly. Based on the Shannon capacity of band- limited waveform AWGN channel with input power constraint, the channel capacity of WSDM is analysed in this paper. Of course, the frequency bandwidth and signal to noise ratio are known in advance. What’s more, how to separate time-frequency mixed signals is the difficult point of WSDM system in practice. In this paper, we take the information optimization in receiver as criterion, and we obtain the objective function based on this criterion. Finally, we provide a linear optimal separating matrix for signal separation of mixed signals by maximizing the objective function. Compared to other signal separation methods, such as blind source separation (BSS) and independent component analysis (ICA) [9]-[11], the proposed method is more feasible and performs better according to computer simulations.
The outline of the paper is as follows. Section 2 presents the system model of WSDM. Section 3 analyses the channel capacity of WSDM. Section 4 describes the information optimization method, which is used to separate the mixed signals. We also give some simulations to check up the proposed method. Finally, Section 5 presents the conclusions.
2. WSDM System Model
WSDM system consists of two parts: mixing system and separating system, as shown in Figure 2. In mixing
![]()
Figure 1.Wireless statistic division multiplexing.
system, the mutual independent sources are transmitted simultaneously in the same frequency band over wireless channel. Meanwhile, time-frequency mixed signals are received by multiple antennas in receiver. In separating system, the source signals can be recovered through appropriate separating algorithm.
In this paper, we assume that the number of sources is equal to that of antennas in receiver. The mathematical model of time-frequency mixed signals is
(1)
where the matrix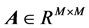 
represents for the channel mixing matrix; 
denotes additive noise vector in wireless channel; 
represents for mutual independent source signals vector;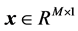 
denotes the observed time-frequency mixed signals vector; 
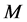is the number of sources.
Put the mixed signals into separating algorithm, and we will derive estimate signals of sources. In this paper, we assume the algorithm is linear, in other words, it is a matrix.
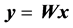(2)
where 
is the linear separating matrix; 
denotes estimate signals vector. The main task in separating system is searching for a linear matrix to make 
approach to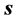 
as much as possible.
3. Channel Capacity of WSDM
As we all know, channel capacity is the elementary and direct property of communication systems. In this paper, we discuss the channel capacity of WSDM when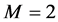
. Then, Equation (1) becomes
(3)
where 
denotes two independent sources; ![]()
represents for vector of mixtures;
![]()
is noise vector, i.e. AWGN in this paper; ![]()
is the channel mixing matrix; ![]()
denotes the transpose. If the power in transmitter is equal to that in receiver, matrix ![]()
should meet the following equation.
![]()
(4)
The information of observed time-frequency mixed signals obtained from sources is
![]()
(5)
where ![]()
is the mutual information between ![]()
and![]()
; ![]()
denotes the entropy of the mixed signals vector; ![]()
is the conditional entropy of ![]()
given![]()
, which means whatever entropy the vector ![]()
has that didn’t come from vector![]()
.
The channel capacity of WSDM system is the maximization of information in (5)
![]()
(6)
According to central limit theorem, the mixed signal ![]()
and ![]()
obey Gaussian distribution. Based on Shannon channel capacity theory, we attain
![]()
(7)
where ![]()
represents for the frequency bandwidth; ![]()
denotes the signal to noise ratio. In a similar way, we can get
![]()
(8)
As a result, under the restraint of (4), the channel capacity of WSDM is
![]()
(9)
The frequency bandwidth efficiency of WSDM is
![]()
(10)
We obtain a closed-form expression for the channel capacity of WSDM system in (9). However, wireless channel is changing all the time, so the parameters in ![]()
is uncertain. Figure 3 shows the frequency bandwidth efficiency of WSDM in different channel conditions. WSDM can achieve good performance under ![]()
condition when ![]()
(over the red curve in Figure 3). When parameters in ![]()
are all the same, WSDM suffers a terrible performance (shown as the green curve).
Compared to traditional multiplexing, such as TDM and FDM, WSDM shows great advantages in frequency bandwidth efficiency, as is shown in Figure 4. In all, WSDM can contribute to the improvement of the utilization of spectrum resources in wireless communications.
![]()
Figure 3. Frequency bandwidth efficiency of WSDM in different channel conditions.
![]()
Figure 4. Frequency bandwidth efficiency of different methods.
4. Channel Capacity of WSDM
How to separate mixed signals effectively is the key point in WSDM system. In this paper, we adopt information optimization criterion and achieve perfect performance. The information of estimate signals got from sources is
![]()
(11)
where ![]()
denotes information of estimate signals. Spread the Equation (2) when ![]()
![]()
(12)
where ![]()
denotes the separating matrix; ![]()
represents for estimate signals vector.
When we optimize![]()
, we can optimize ![]()
and ![]()
respectively.
![]()
(13)
The optimization of ![]()
is equal to that of![]()
.
![]()
(14)
The results of (14) is
![]()
(15)
In the same way, optimize ![]()
and we will get
![]()
(16)
Finally, we attain the expression of separating matrix ![]()
![]()
(17)
where![]()
.
Compared with other separation algorithms, such as that of BSS and ICA, information optimization method achieves more perfect performance, as is shown in Figure 5. Especially at lower SNR, advantage is more obvious. Because the proposed method eliminates the effect of noise as much as possible while BSS and ICA are sensitive to noise.
Choose 4 different voice signals as the sources, as is shown in Figure 6. The sampling frequency is 8000 Hz and the length of data is 20,000. Figure 7 depicts the time-frequency mixed signals. Figure 8 describes estimate signals derived by the proposed method. The above simulations verify the good performance of the proposed method.
![]()
Figure 5. Performance of different separation algorithms.
![]()
Figure 8. Estimate signals derived by the proposed method.
5. Conclusion
In this paper, we analyze the channel capacity of WSDM system. The results indicate the validity in raising frequency bandwidth efficiency. This is a great breakthrough in wireless communications without hesitation. What’s more, we apply information optimization method to separated time-frequency mixed signals. Computer simulations show that the proposed method is more effective than traditional algorithms.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant 61172061 and the Natural Science Foundation of Jiangsu Province in china under Grant BK2011117. The authors would like to thank the reviewers for their insightful comments and helpful suggestions.