Aggregating Qualitative Verdicts: From Social Choice to Engineering Design ()
Received 27 April 2016; accepted 27 May 2016; published 30 May 2016

1. Introduction and Background
At the first glance, problems in social choice and those in engineering design seem to be quite far apart from each other. Social choice theory typically looks for the existence of a consistent social welfare function that is meant to represent the common will or social good of society.
Engineering design aims at choosing a particular design out of a set of alternative options, and this design has the property of best satisfying a certain number of criteria that are deemed relevant in the given context.
During the last decade or so, there have been various papers that examine in some detail the relationship between the individual design engineer and a social planner who wishes to elicit the societal ranking of alternatives.
However, the views on this relationship are by no means congruent. While some authors claim (see, for example, Franssen [1] (2005)) that Arrow’s [2] famous impossibility theorem (1951, 1963) immediately applies to the aggregation problem of the design engineer, other authors such as Scott and Antonsson [3] (1999) and Dym et al. [4] (2002) argue that Arrow’s negative verdict hardly has any importance for decision making in engineering design.
If the former of the two positions described above is correct, rational choice of an optimal design is doomed to failure, at least as long as one remains in an ordinal framework so that preference intensities (on a cardinal scale, for example) are excluded and as long as one insists that all of the conditions that Arrow required be upheld. The latter position comes in various forms. Dym et al. [4] (2002) proposed a method called pairwise- comparison charts that produces results that are equivalent to those obtained by the Borda rank-order method which violates Arrow’s requirement (4) from above, the condition of independence of irrelevant alternatives. Scott and Antonsson [3] (1999) argued that nearly all engineering requirements are of a “single-peaked” nature with less being better than more or vice versa, or closer to a particular reference point or target being better than further away so that Arrow’s condition (2) from above, namely that all logically possible preference rankings should be admissible, is unwarranted. The idea of single-peakedness comes from political theory. As long as all voters evaluate a set of competing candidates on a one-dimensional left-right external scale, the property of single-peakedness may be satisfied quite naturally. However, if the left-right spectrum is no longer preserved between criteria (because some voters, let’s say, judge candidates in relation to their financial or educational background and not their political orientation), this property may no longer be satisfied.
Consider the following multi-criteria decision problem from engineering where the choice of engine is at issue and weight, power-to-weight ratio and cost are the relevant criteria (Table 1).
In this example, criteria 1 and 3 follow the “philosophy” that smaller is better than larger, while criterion 2 is such that larger is preferred to smaller. So according to criterion 1, we obtain that a is better than b which is better than c which again is better than d. Criterion 2 prefers c to b, b to d, and d to a, and criterion 3 finds d best, then a which is followed by b, and c being last. These rankings, taken separately, are very intuitive; taken together, they cannot be arranged in a single-peaked fashion (see also Franssen [1] (2005) for a similar argument).
![]()
Table 1. A multi-criteria decision problem.
Our example shows that Scott and Antonsson’s [3] suggestion apparently does not lead very far as a general way out of the Arrovian dilemma.
It is interesting to note that the problem of an engineer to judge alternative design options is almost identical, from a theoretical perspective, to that of a scientist who has to evaluate alternative new theories that promise to solve a particular question in science, this exercise being based on a set of epistemic values or criteria. This problem was prominently formulated by Kuhn [5] [6] (1962, 1977) who argued that there is not a unique way for doing so (see also Gaertner and Wüthrich [7] (2015)). In the philosophy of science literature, similarly to what we just discussed, one can find the view that Arrow’s result is of direct relevance, but also the position that his negative result is of no greater importance since either single-peakedness is naturally satisfied or that Arrow’s non-dictatorship condition does not necessarily apply, since there always is one criterion or value that dominates all the others.
In the following Section 2, we shall start with an example of a voting procedure that is meant to illustrate our proposed method and then deliver arguments for introducing a common scale or language on which all criteria relevant for a particular design problem should base their preferential judgments. Section 3 discusses the comparability issue across criteria. Section 4 proposes a method for evaluation that is cardinal in character and is known in social choice theory as a scoring method. It has been successfully applied in social and political competition. An axiomatic underpinning is presented which uses the idea of a common scale with qualitative verdicts as a common language. It allows us to formulate in Section 5 a possibility result that, as we hope, may prove useful in engineering design. In this section, we also briefly discuss the situation that there is more than one evaluating engineer. We end with a few concluding remarks in Section 6.
2. An Analogy to Committee Decisions
Imagine you are one of the members of a recruitment committee that has to decide among a certain number of applications for a faculty position. Let us suppose that k candidates are being considered more closely. Let us further assume that the chairman of your committee comes forward with the following procedure. He declares that there are m categories (from “excellent” to “not acceptable”, let’s say, with m − 2 categories in between), with rank scores from m to 1 attached to these categories. The chairperson asks all members of your committee to allocate the k candidates to the m available categories. It is explicitly not required that every member comes up with a strict ordering and that all categories have to be filled by each and every committee member.
Furthermore, the chairperson announces that, as soon as each member has assigned the k candidates to the m categories, he would count the rank numbers assigned to each candidate and then construct a ranking over the k applicants from the highest rank sum to the lowest, the candidate with the highest aggregate sum being the winner. We claim that this aggregation procedure can be made fruitful for design choices in engineering.
In the above scenario, replace the candidates with alternative design options, the members of the committee with certain criteria to be satisfied, and the chairperson with an individual engineer. Furthermore, consider an interval scale with the following equi-distanced categories: “excellent”, “high”, “satisfactory”, “just sufficient”, and “insufficient”.
This structure provides the following set-up for design choice: our engineer considers alternative design options in the light of the set of given criteria. For each criterion, the engineer attaches a qualitative verdict to the alternative options (e.g. “design model D1 is ‘sufficient’ in relation to acceleration”, “design model D2’s acceleration is ‘insufficient’”). The five qualitative verdicts correspond to an interval scale with rank scores. The overall ranking of the design models is determined by the sum of rank scores for each alternative option.
Notice the function that the qualitative verdicts are performing. The verdicts expressed in rank scores constitute a common qualitative scale and represent a cardinalization of the preference orderings over the set of criteria. However, this cardinality is imposed on the ordinal ranking which was formed according to the performance of the various criteria. It is not assumed that the criteria themselves necessarily provide more than ordinal information. It is the imposed cardinal representation which allows intercriteria comparison and, hence, enables us to avoid, as we shall see, an impossibility result à la Arrow. In order to make the cardinal scores for each of the design objects comparable across the set of criteria and thereby to achieve inter-criteria comparability, the process of construction of the scale is of utmost importance. This process can be compared to the creation of a common language that constitutes a unifying basis for comparison. Balinski and Laraki [8] [9] (2007, 2010) argue in a similar way but their own proposal focuses on the median grade within an ordinal framework with no trace of cardinalization.
In order to clarify more concretely our proposed approach, let us refer again to the committee and its members. Each individual has to transform his or her ordinal preference relation ⪰ over the alternative candidates into a cardinal ranking with the requirement that if candidate x, let us say, is at least as good as applicant y, the cardinal rank or score attached to x is at least as high as the rank assigned to y so that for all x, y Î X, the set of all candidates, the following relationship holds: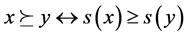 , where s(x) stands for the cardinal value or score attached to x, and likewise for y. This is a very basic requirement in the sense that one must neither lose nor distort ordinal information when one makes a transition from the ordinal to the cardinal world. Furthermore, we postulate that score differences among the different options are meaningful and comparable, so that for four alternatives x, y, z, and w, let us say, a committee member may, for example, come to the conclusion that sn(x) − sn(y) > sn(z) − sn(w), where sn(x) stands for the score assigned to alternative x by committee member n. Note that any affine transformation of these scores with a common positive scale factor over all n does not destroy this comparison of score differences. Coming back to our problem of design comparison, our engineer is assumed to examine the given designs in the light of the set of criteria that are relevant for the problem at stake. More explicitly, the engineer starts for each single criterion with an ordinal ranking over the design objects to be evaluated and then transforms this ranking into a sequence of cardinal scores according to the specified relationship from above. Hereby, we assume, as outlined above, that the engineer can translate the ordinal into the cardinal information for every given criterion in isolation.
, where s(x) stands for the cardinal value or score attached to x, and likewise for y. This is a very basic requirement in the sense that one must neither lose nor distort ordinal information when one makes a transition from the ordinal to the cardinal world. Furthermore, we postulate that score differences among the different options are meaningful and comparable, so that for four alternatives x, y, z, and w, let us say, a committee member may, for example, come to the conclusion that sn(x) − sn(y) > sn(z) − sn(w), where sn(x) stands for the score assigned to alternative x by committee member n. Note that any affine transformation of these scores with a common positive scale factor over all n does not destroy this comparison of score differences. Coming back to our problem of design comparison, our engineer is assumed to examine the given designs in the light of the set of criteria that are relevant for the problem at stake. More explicitly, the engineer starts for each single criterion with an ordinal ranking over the design objects to be evaluated and then transforms this ranking into a sequence of cardinal scores according to the specified relationship from above. Hereby, we assume, as outlined above, that the engineer can translate the ordinal into the cardinal information for every given criterion in isolation.
3. Comparability across Criteria
3.1. The Meaning of Qualitative Grades
The common scale that we are proposing could well be the zero-one interval of the reals, but in many situations, the scale is integer-valued and equi-distanced. Examples of such scenarios are manifold-ranging from wine tasting over figure skating (Balinski and Laraki [8] [9] (2007, 2010)) to the evaluation of research proposals, an admission to some higher education and the choice of a best candidate in relation to a job opening, as in our earlier example. This common language of qualitative grades introduces some inter-criterion comparability in the sense that, across the various criteria, the verdict “excellent” means “excellent” and “insufficient” means “insufficient”.
To be clear, the grade “excellent”, for example, does not necessarily fulfil the same list of prerequisites for each and every criterion. For one criterion, the grade “excellent” may hardly ever be given or reached (e.g. susceptibility to a break-down in the case of a new car design), another criterion may achieve the predicate “excellent” fairly easily (e.g. noise reduction). What we have as information is a judgment that comes from each criterion. However, if two criteria attach the judgment “excellent” to a particular design object, then this should be taken at face value. To argue that “excellent” according to one criterion corresponds to only “sufficient” in relation to another criterion may critically undermine the required inter-criteria comparability and may also provoke a controversial debate, once not one but several engineers are engaged in the evaluation of alternative options. In other words, the grades that are assigned to the alternative design options have a meaning that is absolute across the criteria.
One could argue that in engineering, grades such as “excellent” or “sufficient” are not always useful since much more fine-grained verdicts are available. This is undoubtedly true for certain characteristics but not for others. In the case of judging alternative car designs, for example, velocity, acceleration and fuel consumption are features such that different performances can be assigned to particular points on a ratio scale. Par contre, comfort, image and aesthetic aspects in relation to body shape and colour but also features such as the afore mentioned susceptibility to break-down are properties that are more difficult to quantify on some scale. What may make the evaluative exercise of the engineer more complex is that an index that reflects an outstanding acceleration, for example, will perhaps not be considered excellent in relation to an extremely high fuel consumption and a low fuel consumption will not be viewed as excellent in the light of a very modest degree of acceleration. So the design engineer may consider interdependencies among various criteria whereas for criteria such as, for example, fuel consumption and comfort, a separability argument may apply.
We believe, however, that these complications are not insurmountable.
3.2. The Common Scale as an Inter-Attribute Device
To repeat, what is essential for the aggregation procedure that we shall describe and characterize in the next section is that the common scale is properly understood as an inter-attribute device to link or combine different dimensions. Without the latter, it would just make no sense to use integer values on a scale as an expression of qualitative verdicts that are assigned to a given set of criteria deemed relevant for alternative design options. Clearly, to conceive such a common scale is by no means an easy task that the decision maker has to perform, and it will, quite naturally, depend on the type of design considered. It may be more fine-grained in some cases of design evaluation and less fine-grained in others.
What we propose is that an engineer performs the following mental exercise. Given a common scale for all relevant criteria, he assigns ratings to performance under the various criteria. If design D1 gets the attribute “excellent” for criterion 1 and “satisfactory” for criterion 2, and for design D2, the rating is just the other way round, the two designs are ranked equally. If life expectancy as criterion 1 is considered more valuable than load capacity, one may want the performance under criterion 1 to count twice as much. This can be achieved by putting this criterion twice on the list of relevant criteria or, even better if possible, another criterion is added to the list which is closely related to criterion 1. In the case of cars as discussed, the expected price or value of this car on the second-hand market or the cost of maintenance may be such an additional criterion.
4. The Formal Framework
Let X be the universal set of design options containing a finite number of elements. Let N be the set of criteria deemed relevant with n > 1. Let E = {1,  , E}, with the cardinality of this set being larger than one, be a set of given positive integers from 1 to E. These integers will in most cases be equally distanced and are thought to represent qualitative statements thus constituting a common language of evaluation, as outlined in the previous section. A scoring function si: X ® E is chosen for each criterion i Î N, such that, for all x Î X, si(x) indicates the score that criterion i assigns to x. Let Si be the set of all possible scoring functions for criterion i. As explained in the last section, the statement how well or how badly each criterion fares has to be inserted in the commonly given scale constituted by set E so as to accurately represent its ´value for the design object considered.
, E}, with the cardinality of this set being larger than one, be a set of given positive integers from 1 to E. These integers will in most cases be equally distanced and are thought to represent qualitative statements thus constituting a common language of evaluation, as outlined in the previous section. A scoring function si: X ® E is chosen for each criterion i Î N, such that, for all x Î X, si(x) indicates the score that criterion i assigns to x. Let Si be the set of all possible scoring functions for criterion i. As explained in the last section, the statement how well or how badly each criterion fares has to be inserted in the commonly given scale constituted by set E so as to accurately represent its ´value for the design object considered.
Let P be the set of all orderings over X. A profile 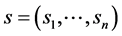 is a list of scoring functions, one for each criterion. An aggregation rule f is defined as a mapping:
is a list of scoring functions, one for each criterion. An aggregation rule f is defined as a mapping: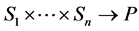 . Let
. Let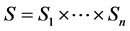 . Mapping f is said to be an E-based scoring rule, to be denoted by fE, iff, for any s Î S, and any x, y Î X,
. Mapping f is said to be an E-based scoring rule, to be denoted by fE, iff, for any s Î S, and any x, y Î X,
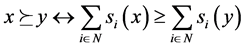 , where ⪰ = f(s). The asymmetric and symmetric parts of ⪰ will be denoted by
, where ⪰ = f(s). The asymmetric and symmetric parts of ⪰ will be denoted by 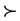
and ~, respectively. For any s, s' Î S, any i, j Î N and any x, y Î X, we say that s and s' are (i, j)-variant with respect to (x, y) if 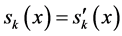 and
and 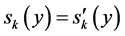 for all k Î N − {i, j}.
for all k Î N − {i, j}.
We now introduce two properties to be imposed on an aggregation rule f.
Dominance (D). For all s Î S and all x, y Î X, if si(x) ³ si(y) for all i Î N, then x ⪰ y and if si(x) ³ si(y) for all i Î N and sj(x) > sj(y) for some j Î N, then x 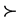 y.
y.
Cancellation
Independence
(CI). For all s, s' Î S, all x, y Î X and all i, j Î N, if s and s¢ are (i,j)-variant with respect to (x, y), 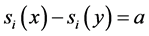 ,
,  ,
, 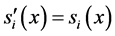 ,
,  ,
, ![]() and
and ![]() where g = min(a, b) when a ³ 0 and b ³ 0 and g = max(a, b) when a < 0 and b < 0, then x ⪰ y « x ⪰¢ y, where ⪰ = f(s) and ⪰¢ = f(s').
where g = min(a, b) when a ³ 0 and b ³ 0 and g = max(a, b) when a < 0 and b < 0, then x ⪰ y « x ⪰¢ y, where ⪰ = f(s) and ⪰¢ = f(s').
Condition D is a simple vector dominance condition. It requires that, in ranking two design models x and y, if the score assigned to x by each criterion i Î N is at least as large as the score assigned to y by the same criterion i, then x must be ranked at least as high as y by the evaluating engineer, and if in addition, some criterion assigns a higher score to x than to y, then x must be ranked higher than y.
Condition CI makes use of the fact that for any pair of alternatives, rank differences of opposite sign can be reduced without changing the aggregate outcome of the ranking procedure. This reduction procedure is performed in a stepwise fashion, starting with any two design options x and y, let’s say, and picking any two criteria whose rank differences for x and y are of opposite sign. The “net” rank difference between x and y for this pair of criteria is determined. Then another criterion is picked whose rank difference for x and y is opposite in sign to the net rank difference of the first two criteria. The new net rank difference for x and y is calculated and the next criterion is picked whose rank difference again is opposite in sign to the just determined net rank difference with respect to x and y, if there is still one such criterion, and so on.
Such a step-wise cancellation procedure can be illustrated by the following simple scheme where two designs D1 and D2 are evaluated via three criteria. One starts with criteria 1 and 2 whose rank differences in relation to D1 and D2 are of opposite sign, calculates the “net” rank difference and then moves on to the third criterion, where, again, a rank difference of opposite sign occurs. The final outcome in this case is an equivalence between the two designs (Table 2).
In Condition CI, vectors s and s' define scoring profiles that are aggregate-rank equivalent with respect to any pair of objects to be evaluated. We call s' an s-reduced scoring profile. Condition CI therefore demands that f(s) and f(s') order any x and y in exactly the same way. Note that Condition CI makes an implicit assumption about an inter-criterion comparison of scores for which a common language is required.
5. A Possibility Result for Cardinal Scores
Dominance and Cancellation Independence allowed Gaertner and Xu [10] (2012) to provide a simple characterization of the E-based aggregation rule.
THEOREM. f = fE if and only if f satisfies the properties of Dominance and Cancellation Independence.
A proof of this result can be found in Gaertner and Xu [10] (2012). The grading system that we propose is similar to the Borda count in the sense that for each candidate or option to be evaluated, the aggregate rank or score sum is being calculated, with the highest aggregate score sum(s) determining the winning design(s). But notice that it is not the Borda count since in its original version, the latter required that if there are m objects to be evaluated, these should be arranged in a strict or linear order, either descending or ascending within each criterion. The method that we propose does not require this. A particular criterion may, for example, rate several options as good and several other options as just acceptable but may find that no object is either excellent or very good or, at the other end, unacceptable. In other words, and in contrast to the Borda procedure, for one or several criteria the common scale may have several empty cells. This means that each criterion possesses its own scoring function that attaches grades to the objects within the given scale. This shows that the method just characterized allows the expression of preference intensities to a much larger or more refined degree than is possible within the Borda scheme.
Our model neither runs into Arrow’s impossibility result nor does it make restrictions which, at a closer look, turn out to be highly implausible. The method uses cardinal scores, though, and if this is a knock-out criterion, then this procedure is doomed to be beyond limits. Clearly, the scoring rule proposed has to be weighed against the pairwise comparison charts (Dym et al. [4] (2002)). It has to be weighed against Pugh’s [11] (1990) method, against some method based on von Neumann and Morgenstern’s [12] (1953) expected utility approach (see Hazelrigg [13] (1999)), and still other methods.
Our theorem establishes, for the evaluating engineer, an ordering over the set of alternative design objects once this person has consented to the common language as we assumed. Should there be more than one decision-maker, various methods are available in order to obtain an overall verdict among the group of evaluators. All of these rules violate at least one of Arrow's requirements (see, for example, Gaertner [14] [15] (2009, 2016)). The Borda rule is one candidate to aggregate a profile of ordinal rankings, approval voting (Brams and Fishburn [16] (1983)) would be a second, plurality voting a third. The Borda method has a large advantage over the other two rules, namely, its aggregation procedure uses a lot of positional information that both plurality and approval voting totally ignore. While the plurality rule restricts itself to using information on the top element within each person's evaluation only so that the ranking of all other options is blatantly ignored, approval voting implicitly constructs two indifference classes, the set of acceptable options and the set of unacceptable alternatives, with no further differentiation in either set. One may therefore consider the degree of differentiation among the alternatives as too low and, consequently, as unsatisfactory.
It may be surprising for the reader to see that in the situation of several engineers who are about to evaluate alternative design objects, we propose methods which use ordinal information only. We could have proposed in this case that all evaluators apply the scoring method laid out above and characterized in the theorem. This
![]()
Table 2. A step-wise procedure for three criteria.
would have required, however, that all individuals involved agree to the same grading structure, be it fine- grained or coarse-grained. One can, of course, make this assumption but this may be unduly restrictive. What our aggregation procedure leads to, namely that x ⪰ y ↔![]() , is an ordinal ranking based on the grading structure of one particular person. Aggregating this ordinal information across engineers allows that those involved in the evaluation need not necessarily resort to the same grading system but that each person can choose his or her own structure. As we mentioned before in the context of a single engineer, one evaluator may “easily” attach the grade “excellent” to a design object and hardly ever choose the verdict “fail”, whereas others may be much more critical and almost never pick the predicate “excellent”, for example. All this is possible and permissible when an aggregation across persons is done where one just uses ordinal rankings as the outcome of each person’s grading task.
, is an ordinal ranking based on the grading structure of one particular person. Aggregating this ordinal information across engineers allows that those involved in the evaluation need not necessarily resort to the same grading system but that each person can choose his or her own structure. As we mentioned before in the context of a single engineer, one evaluator may “easily” attach the grade “excellent” to a design object and hardly ever choose the verdict “fail”, whereas others may be much more critical and almost never pick the predicate “excellent”, for example. All this is possible and permissible when an aggregation across persons is done where one just uses ordinal rankings as the outcome of each person’s grading task.
6. Concluding Remarks
The aggregation rule that is characterized in this paper is a general version of what Smith [17] (2000) called “range voting”. The latter procedure has been applied in committee decisions and, to the best of our knowledge, in smaller political elections. The aggregation rule we proposed satisfies a couple of “nice” properties. It fulfils Arrow’s unrestricted domain condition so that it is not necessary to assume that all the criteria that are considered essentially order a set of design objects in a single-peaked or a single-troughed way or in some other fashion with a uniform structure.
Our procedure treats criteria equally and also treats objects neutrally. The suggested procedure is sensitive towards the degree of criteria fulfilment. This is, in social choice theory, denoted as a form of positive responsiveness or positive association in the sense that a unilateral change in the fulfilment of some criterion in favour of design object x, let’s say, should be reflected on the aggregate level in the same and not in the opposite direction, in other words should be beneficial for x.
Our model also satisfies a property that is sometimes called consistency, at other times reinforcement, demanding that if the set of criteria is split up into two parts and a certain design object wins in both subsets, then this object must also win in relation to the complete set of criteria.
Let us emphasize again that different criteria can rank or rather assign scores to the given objects in completely different ways as explained in the previous sections. We consider this as an advantage since the single criterion has more flexibility “to articulate its preference”, i.e., it has more flexibility to express to what degree or extent it finds itself represented among the different design objects under consideration. It is our conviction and hope that the cardinal approach proposed in this paper will be a fruitful way to evaluate alternative design objects. The final verdict, of course, has to come from the engineering profession.
Acknowledgements
I am grateful for the comments and suggestions from an anonymous referee.