Received 7 January 2016; accepted 3 May 2016; published 6 May 2016

1. Introduction
Canonical Lagrangian has been studied in the context of classical mechanics, quantum field theory and other branches of physics. The standard form of canonical Lagrangian density is given by
 (1)
(1)
Here 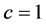 and also action S is dimensionless then, Lagrangian density
and also action S is dimensionless then, Lagrangian density 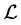 has dimension of
has dimension of 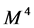 and hence dimension of
and hence dimension of 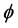 is M (here M stands for mass). Also we are considering the case of one time and one space dimension. Thus
is M (here M stands for mass). Also we are considering the case of one time and one space dimension. Thus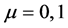 , where
, where 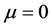 corresponds to time coordinate t, and
corresponds to time coordinate t, and  corresponds to space coordinate x. Here the metric tensor
corresponds to space coordinate x. Here the metric tensor 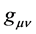 is diagonal, and is given by
is diagonal, and is given by
 (2)
(2)
In this framework, Lagrangian density (1) can be written as
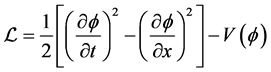 (3)
(3)
Here kinetic energy term  is quadratic. Lagrangian density (1) has been extensively studied in the context of quantum field theory, theory of phase transition and other branches of physics [1] - [5] . In recent years, non canonical Lagrangian density has been used in the inflationary cosmological models [6] - [8] (see ref. [9] for further details). In the context of cosmological model, even in absence of any potential energy term, a general class of non-standard (i.e., non-quadratic) kinetic energy terms
is quadratic. Lagrangian density (1) has been extensively studied in the context of quantum field theory, theory of phase transition and other branches of physics [1] - [5] . In recent years, non canonical Lagrangian density has been used in the inflationary cosmological models [6] - [8] (see ref. [9] for further details). In the context of cosmological model, even in absence of any potential energy term, a general class of non-standard (i.e., non-quadratic) kinetic energy terms , for a scalar field
, for a scalar field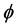 , can drive an inflationary evolution of the same type as the usually considered potential driven inflation. The mathematical form of non canonical Lagrangian density is given by the following equation:
, can drive an inflationary evolution of the same type as the usually considered potential driven inflation. The mathematical form of non canonical Lagrangian density is given by the following equation:
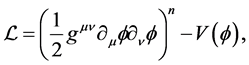 (4)
(4)
where ![]() is the potential and n is an integer. For
is the potential and n is an integer. For![]() , we get the usual Lagrangian of the scalar field theory. Also, note that the Equation (4) is Lorentz invariant for any value of n. The purpose of this work is to obtain the exact solution of Equation (4) in (1 + 1)-dimension for
, we get the usual Lagrangian of the scalar field theory. Also, note that the Equation (4) is Lorentz invariant for any value of n. The purpose of this work is to obtain the exact solution of Equation (4) in (1 + 1)-dimension for![]() , and for the different potentials. For
, and for the different potentials. For![]() , Equation (4) takes the form
, Equation (4) takes the form
![]() (5)
(5)
Also, we are using natural units in which ![]() and action is dimensionless. In this unit
and action is dimensionless. In this unit ![]() is dimensionless. The corresponding equation of motion is given by
is dimensionless. The corresponding equation of motion is given by
![]() (6)
(6)
Thus the Lagrangian density is given by
![]() (7)
(7)
From here one can see that the kinetic energy is non-quadratic and that’s why the Lagrangian is known as non-canonical Lagrangian. The corresponding equation of motion is given by
![]() (8)
(8)
Here ![]() represents the time derivative of field and
represents the time derivative of field and ![]() represents the spatial derivative. Note that the equation of motion remain second order. Also, for a Lorentz invariant system once a static solution is known, moving solutions are obtained by transforming to a moving coordinate system [1] (we are interested in solitary and periodic wave solutions). Now for static case, the equation of motion becomes
represents the spatial derivative. Note that the equation of motion remain second order. Also, for a Lorentz invariant system once a static solution is known, moving solutions are obtained by transforming to a moving coordinate system [1] (we are interested in solitary and periodic wave solutions). Now for static case, the equation of motion becomes
![]() (9)
(9)
Multiplying both sides by ![]() and integrating with respect to x, we obtain
and integrating with respect to x, we obtain
![]() (10)
(10)
where C is constant of integration. Let ![]() and
and ![]() vanishes at
vanishes at ![]() and hence
and hence![]() . Thus finally we obtain
. Thus finally we obtain
![]() (11)
(11)
For ![]() in Equation (4), the corresponding equation of motion is given by
in Equation (4), the corresponding equation of motion is given by
![]() (12)
(12)
In the next section we will solve Equation (11) for some specific potentials. Also, Equation (11) cannot be solved for every potential. We will consider only those potentials for which Equation (11) can be integrated.
2. Solutions
In this section we are going to solve Equation (11) for the following potentials.
Case I: Let us first consider the potential
![]() (13)
(13)
where ![]() is real constant and its dimension is
is real constant and its dimension is![]() . This potential is used in the theory of phase transition and is taken from reference [1] . For this potential, Equation (11) takes the form
. This potential is used in the theory of phase transition and is taken from reference [1] . For this potential, Equation (11) takes the form
![]() (14)
(14)
After integrating this equation, we obtain
![]() (15)
(15)
where ![]() is constant of integration. To solve the left hand integral, we substitute
is constant of integration. To solve the left hand integral, we substitute ![]() and after solving this integral, we obtain
and after solving this integral, we obtain
![]() (16)
(16)
For time dependent case, the corresponding solution can be obtained by Lorentz transformation
![]() (17)
(17)
and hence
![]() (18)
(18)
From this solution one can see that, for ![]() we obtain periodic solution and for
we obtain periodic solution and for![]() , we obtain hyperbolic solution. The hyperbolic solution diverges for large x and t. Now the energy of the field is given by
, we obtain hyperbolic solution. The hyperbolic solution diverges for large x and t. Now the energy of the field is given by
![]() (19)
(19)
where ![]() is energy density and is given by
is energy density and is given by
![]() (20)
(20)
where ![]() is momentum density and
is momentum density and ![]() is time derivative of the field. Here
is time derivative of the field. Here
![]() (21)
(21)
where ![]() is spatial derivative of the field. Using Equations ((20) and (21)), we obtain
is spatial derivative of the field. Using Equations ((20) and (21)), we obtain
![]() (22)
(22)
![]() (23)
(23)
For static case, we obtain
![]() (24)
(24)
Using Equation (11), we get
![]() (25)
(25)
Now
![]() (26)
(26)
and hence
![]() (27)
(27)
Note that![]() , otherwise energy density becomes imaginary. The total energy is given by
, otherwise energy density becomes imaginary. The total energy is given by
![]() (28)
(28)
For time dependent case, energy density is given by
![]() (29)
(29)
For![]() , and for the given potential Equation (16), we obtain from Equation (12) the following solution
, and for the given potential Equation (16), we obtain from Equation (12) the following solution
![]() (30)
(30)
which is a kink solitary wave solution [1] for![]() . Thus in this case solution exist for
. Thus in this case solution exist for![]() . Energy density in this case is given by
. Energy density in this case is given by
![]() (31)
(31)
The energy density is localised near![]() . According to the definition of [1] , localised solutions are those solutions to the field equation whose energy density
. According to the definition of [1] , localised solutions are those solutions to the field equation whose energy density ![]() at any finite time t is localised in space and falls to zero at spatial infinity.
at any finite time t is localised in space and falls to zero at spatial infinity.
Case II: Here we will consider the potential of the form
![]() (32)
(32)
In this case, the solution of time independent field equation is given by
![]() (33)
(33)
Note that this solution is a solitary wave solution for![]() . Similarly, the corresponding solution of time dependent case is given by
. Similarly, the corresponding solution of time dependent case is given by
![]() (34)
(34)
The energy density of time independent case is given by
![]() (35)
(35)
and the energy density of time dependent case is given by
![]() (36)
(36)
Thus the energy density is localised.
3. Concluding Remarks
In this work we have discussed the non-canonical lagrangian for different kinds of potential. We have obtained the periodic and solitary wave solutions. A comparison is also made between the solutions of canonical and non-canonical lagrangian. As one can see that for Equation (16), the solution exists only when ![]() whereas, for the same potential and for canonical Lagrangian, the solution exists for
whereas, for the same potential and for canonical Lagrangian, the solution exists for![]() . Also the solution of non- canonical lagrangian is periodic and canonical lagrangian admits the solitary wave solution. Similarly for the potential (32), the non-canonical lagrangian admits the solitary wave solution for
. Also the solution of non- canonical lagrangian is periodic and canonical lagrangian admits the solitary wave solution. Similarly for the potential (32), the non-canonical lagrangian admits the solitary wave solution for![]() . Although non-canonical Lagrangian has been used in the inflationary model, the result obtained in this work may be used to explain the phenomena of phase transition and other quantum field theoretic model.
. Although non-canonical Lagrangian has been used in the inflationary model, the result obtained in this work may be used to explain the phenomena of phase transition and other quantum field theoretic model.
Acknowledgements
We would like to thank Sanil Unnikrishnan for helpful discussions.
NOTES
![]()
*Corresponding author.