Hopf Modules in the Category of Yetter-Drinfeld Modules

Yanmin Yin

Department of Mathematics, Shandong Jianzhu University, Jinan, China.

DOI: 10.4236/am.2016.77058                

Abstract

We give the Fundamental Theorem for Hopf modules  in the category of Yetter-Drinfeld modules , where L is a quasitriangular weak Hopf algebra with a bijective antipode. We also show that H* has a right H-Hopf module structure in the Yetter-Drinfeld category. As an application we deduce the existence and uniqueness of right integral from it.

Keywords

Weak Hopf Algebra, Hopf Module, Fundamental Theorem

Received 8 August 2015; accepted 24 April 2016; published 27 April 2016

1. Introduction

Weak Hopf algebras were introduced by G. Böhm and K. Szlachányi as a generalization of usual Hopf algebras and groupoid algebras [1] [2] . A weak Hopf algebra is a vector space that has both algebra and coalgebra structures related to each other in a certain self-dual fashion and possesses an analogue of the linearized inverse map [3] - [5] . The main difference between ordinary and weak Hopf algebras comes from the fact that the comultiplication of the latter is no longer required to preserve the unit (equivalently, the counit is not requires to be a homomorphism) and results in the existence of two canonical subalgebras playing the role of “non- commutative bases”.

Paper [6] was shown what is a weak Hopf algebra in the braided category of modules over a weak Hopf algebra. In [7] we prove a Fundamental Theorem of Hopf modules for the categorical weak Hopf algebra motivation to study quasitriangular weak Hopf algebras is the so-called biproduct construction and interpreted in the terms of braided categories. More precisely, we are interested in a specific type of quaitriangular weak Hopf algebras.

we prove the Fundamental Theorem for Hopf modules in the category of Yetter-Drinfeld modules according to the fact that the matrix R gives rise to a natural braiding for and. Furthermore is also a right H-Hopf module in the category Yetter-Drinfeld modules. Using this result we obtain the existence and uniqueness of integrals for a finite dimensional weak Hopf algebra in.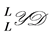

2. Preliminaries

Throughout this paper we use Sweedler’s notation for comultiplication, writing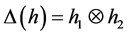. Let k be a fixed field and all weak Hopf algebras are finite dimensional.

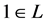Definition 1. A weak Hopf algebra is a vector space L with the structure of an associative unital algebra with multiplication and unit and a coassociative coalgebra 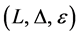with comultiplication and counit such that

1) The comultiplication is a (not necessarily unit-preserving) homomorphism of algebras such that

2) The counit satisfies the following identity

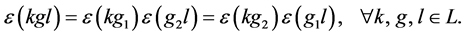
3) There is a linear map called an antipode, such that, for all

The linear map defined in the above equations are called target and source counital maps and denoted by and respectively:

For all, we have

We will briefly recall the necessary definitions and notions on the weak Hopf algebras.

Definition 2. A quasitriangular weak Hopf algebra is a pair where L is a weak Hopf algebra and (called the R-matrix) satisfying the following conditions:

for all, where denotes the conditions apposite to,

where, etc. as usual, and such that there exits with where we write. By [3] , we can obtain the following results.

Proposition 2.1. For any quasitriangular weak Hopf algebra, we have

3. Weak Hopf Algebras in the Yetter-Drinfeld Module Category

Let L be a quasitriangular weak Hopf algebra with a bijective antipode. Suppose H is a weak Hopf algebra in. Paper [7] show that H is also a weak Hopf algebra in with a left L-coaction via . Bing-liang and Shuan-hong introduce the definition of Weak Hopf algebra in the braided monoidal category in [6] . Moreover they have showed that if H is a finite-dimensional weak Hopf algebra in, then its dual is a weak Hopf algebra in.

Definition 3. Let be a quasitriangular weak Hopf algebra. An object is called a weak bialgebra in this category if it is both an algebra and a coalgebra satisfying the following conditions:

1) and are not necessarily unit-preserving, such that

2) H is a left L-module algebra and left L-module coalgebra if H is a left L-module via such that

3) H is a left L-comodule algebra and left L-comodule coalgebra if H is a left L-comodule via such that

4) Furthermore, H is called a weak Hopf algebra in if there exists an antipode (here S is left L-linear and left L-colinear i.e., S is a morphism in the category of) satisfying

Similar to the definition of weak Hopf algebra, we denote If one can obtain. According to the definitions of one obtains explicit expressions for these coproducts

Paper [7] give the following results:

Proposition 3.1. Suppose H is a weak Hopf algebra in. For all we have the identities

Since a weak Hopf algebra H in the weak Yetter-Drinfeld categories is both algebra and coalgebra, one can consider modules and comodules over H. As in the theory of Hopf algebras, an H-Hopf module is an H-module which is also an H-comodule such that these two structures are compatible (the action “commutes” with coaction):

Definition 4. Let H be a weak Hopf algebra in. A right H-Hopf module M in is an object such that it is both a right H-module and a right H-comodule via and the following equations hold for:

1)

2)

3)

4)

5)

We remark that is a right H-module by and a right H-comodule. The condition (1) means that the H-comodule structure is H-linear, or equivalently the H-module structure map is H- colinear. Also, (4) (resp. (2)) is L-colinear (resp. L-linear); (3)(resp. (5)) is L-colinear (resp. L-linear).

Example 3.2. H itself is a right H-Hopf module (in) in the natural way. If V is an object in, then so is by and. It is also both a right H-module and a right H-comodule by and. One easily checks that is an right H-Hopf module.

when H is a weak Hopf algebra in and M a right H-Hopf module in, we prove the Fundamental Theorem 3.3 [7] . Furthermore we will show is a L-subcomodule of M.

Applying we obtain

For we do a calculation:

This implies that. So.

It is clearly to prove F is a left L-colinear by the following equation

Furthermore we can obtain the Structure Theorem for right H-Hopf modules in the category of Yetter- Drinfeld modules.

Theorem 3.3. If H is a weak Hopf algebra in and M is a right H-Hopf module in, is defined as above. Then

1) Let. Then. If and, Then and.

2) The map is an isomorphism of Hopf modules. The inverse map is given by.

4. Fundamental Theorem for H^* in

In [4] has the contragredient left L-module structure by

Since H is a finite-dimensional left L-comodule, has the transposed right L-comodule structure and so it becomes a left L-comodule via

i.e. Now assume that H is finite-dimensional. We will show that becomes a right H-Hopf module in. First is a right H-module by

Second, is a right H-comodule using the identification,

as follows:

That is means

Proposition 4.1. is a right H-comodule by.

Proof. Now for, we have

It implies that.

Accord to we have. Applying the equality

we obtain

Hence. Thus becomes a right H-comodule.

Theorem 4.2. With the notation as above, then is a right H-Hopf module in. Moreover,

.

Proof. Now we prove that is a right H-Hopf module. First we will show that

Since for,

Next we want to check for. Since for

Applying the equality for

It implies that. Using the equality

we compute

Finally we show that. Since for

From all above, is a right H-Hopf module in.

Applying Theorem 4.2 we can obtain the following result.

Corollary 4.3. is defined a right H-Hopf module in as above, then.

5. Applications

As a consequence the space of coinvariants of the finite dimensional Hopf algebra is free of rank one. This is the case for the weak Hopf algebra in the category of the Yetter-Drinfeld modules.

Theorem 5.1. If H is a finite-dimensional weak Hopf algebra in. Then

1)..

2) The map is an right H-module and an right H-comodules isomorphism. In particular H is a Frobenius weak Hopf algebra with Frobenius map.

3) There exist a right integral t in H, and a group-like elment in L such that for all

a),

b),

c)

d), for all.

4) The map is a left L-semilinear and a left L-semicolinear in the sense that for all ,

Proof. 1) Since is a right H-Hopf module in, we have,. Since, it follows that.

2) Choose. Then by (1) is an right H-modules and an right H-comodules. Thus H is Frobenius weak Hopf algebra.

3) a) Since, there is a unique element t in H such that, i.e.. For all we have It follows that

. So t is a right integral in H.

b) We remark that for all from Theorem 3.3. This implies,

i.e. for some, by.

c) From Theorem 3.3 we have is a right L-comodule, i.e.. By

we can obtain for some group-like element in L. This implies that .

d) Applying we have

This means, for all.

4) For all we have

This implies.

Acknowledgements

The author would like to thank the referee for many suggestions and comments, which have improved the overall presentations.

Funding

Research supported by the Project of Shandong Province Higher Educational Science and Technology Program

(J12LI07) and the Project of National Natural Science Foundation of China (51078225).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bohm, G., Nill, F. and Szlachányi, K. (1999) Weak Hopf Algebras I. Integral Theory and C*-Structure. Journal of Algebra, 221, 385-438. http://dx.doi.org/10.1006/jabr.1999.7984
[2]	Caenpeel, S, Wang, D.-D. and Yin, Y.-M. (2005) Yetter-Drinfeld Modules over Weak Bialgebras. Annali Dell’universitia DI Ferrarà, Sezione VII-Scienze Matematiche, 51, 69-98.
[3]	Kadison, L. and Nikshych, D. (2001) Frobenius Extensions and Weak Hopf Algebras. Journal of Algebra, 244, 312-342. http://dx.doi.org/10.1006/jabr.2001.8911
[4]	Takeuchi, M. (1998) Hopf Modules in Yetter-Drinfeld Categories. Communications in Algebra, 26, 3057-3070. http://dx.doi.org/10.1080/00927879808826327
[5]	Bohm, G. (2000) Doi-Hopf Modules over Weak Hopf Algebras. Communications in Algebra, 28, 4687-4689.
[6]	Shen, B.-L. and Wang, S.-H. (2009) Weak Hopf Algebra Duality in Weak Yetter-Drinfeld Categories and Applications. Internation Electeronic Journal of Algebra, 6, 74-94.
[7]	Yin, Y.-M. and Zhang, M.-C. (2011) Hopf Modules in the Braided Monoidal Category LM. Le Matematiche, LXVI, 81-92.