Bias and Mean Square Error of Reliability Estimators under the One and Two Random Effects Models: The Effect of Non-Normality ()
Received 14 February 2016; accepted 23 April 2016; published 26 April 2016

1. Introduction
Statistics is the science of transforming data into information and knowledge. Therefore producing reliable information requires error free data. Measurement errors can seriously affect statistical analysis and interpretation; it therefore becomes important to quantify the magnitude of such errors by calculating what is known as “reliability coefficient” and assessing its statistical properties. The topic of reliability has gained much attention in the literature as evidenced in the books by Dunn [2] [3] , and the recent reviews by Shoukri et al. [4] and Shoukri [5] . As a general feature of this coefficient, it must distinguish within-subject variation from variation between subjects.
A widely recognized index that possesses this property is the intraclass correlation coefficient (ICC) defined as the proportion of between-subject variation relative to the total variation. In the most frequently adopted design, k subjects are each rated by the same n raters (for inter-rater reliability). A similar approach, however, can also be adopted when a single subject is assessed repeatedly on each of several occasions (test-retest reliability), or when replicates consisting of different occasions are taken on different subjects by a single rater [6] . In each of these cases, and for continuous and categorical assessments, Fisher [7] showed that r can be estimated from an appropriate one-way analysis of variance (ANOVA).
There are numerous versions of the intraclass correlation coefficient (ICC) that can give quite different results when applied to the same data. Each form is appropriate for specific situations defined by the experimental design and the conceptual intent of the study. The differences among these forms and their applications were discussed in Shrout and Fleiss [8] , and McGraw and Wong [9] . Shrout and Fleiss [8] provided specific guidelines for choosing the appropriate form of the ICC by adopting two linear additive models. The fundamental question is: which appropriate statistical model for the reliability study, may be selected to address the questions of interest.
Much of the work in reliability studies focused on the estimation (point and interval), hypothesis testing, and sample size requirements to achieve certain power [10] and or maximizing the precision of estimation under cost constraint [11] .
Only recently the issue of correcting the ICC for bias, under the one-way ANOVA was investigated. Assuming the normality of the distribution of scores, Atenafu et al. [1] investigated the issues related to bias correction of the ANOVA estimator of ICC from the one-way layout. The authors investigated the effect of non-normality through Monte-Carlo simulations by generating data from known skewed distributions.
This article has two-fold objectives: First, under the one-way ANOVA, we evaluate the bias, the variance (and hence the mean square error) of the ICC when the assumption of normality is not tenable. We further investigate the effect of non-normality on the sample size requirements to achieve certain levels of power on specific null hypotheses on the reliability parameter for a given level of type I error. Second, under the two-way ANOVA we derive the first order approximation for the bias and the variance of the ICC. This allows for the comparison between the Wald confidence interval and other proposed confidence intervals. We analyze data of two examples using the R package.
The paper is structured as follows: In Section 2 we derive analytic expressions for bias and variance of ICC when the assumption of normality is not satisfied. In Section 3 we extend our approach to the case of two-way data layout. We obtain analytic expressions for bias and variance of ICC, and construct a Wald’s type confidence interval. Moreover we evaluate the empirical power using simulations. In Section 4 we introduce two examples and assess the accuracy of the first order approximation for bias and variance using the bootstrap technology for the two-way model. We discuss the results in Section 5.
2. The Effect of Non-Normality on the Bias and Variance of the One-Way ANOVA Estimator of the Reliability Coefficient
In most interrater reliability study, each of a random sample of k subjects is rated independently by n raters. There usually are two situations that are of interest to us:
1) Each subject is rated by asset n different raters, randomly selected from a larger population of raters.
2) A random sample of n > 1 raters is selected from a larger population, and each judge rates each subject, that is, each judge rates k subjects. We shall assume that the number of raters is less than the number of subjects.
Conceptually the two situations should produce close estimates of the ICC, but components of variations in the scores should appropriately be specified to avoid misspecification bias. Each of the postulated models specifies the decomposition of a rating made by the jth rater on the ith subject in terms of various effects. In this paper we consider the decomposition into subject component, rater component and random error component. Depending on the way the study is designed, different assumptions are made about the effects, and the structure of the corresponding ANOVA will be different.
We start by specifying the simplest design used to assess the reliability sets of scores; namely the one-way random effect model. Suppose that we have k subjects and we would like to take n measurements by a single device. How can we assess the consistency of the set of measurements taken from each subject? The one-way model stipulates that:
 (1)
(1)
The Yij is the jth measurement taken on the ith subject, μ is the bias, bi is the subject effect, and eij is a random measurement error, assumed independent of bi where 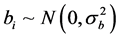 and
and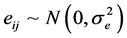 . We assume that bi and eij are mutually independent random variables. Clearly,
. We assume that bi and eij are mutually independent random variables. Clearly, 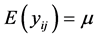 ,
, 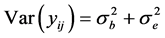 , and
, and

Therefore the reliability coefficient, or the intraclass correlation coefficient (ICC) is defined as:

The reliability estimate of ρ is obtained once suitable estimate of the components of variance are obtained.
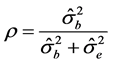 (2)
(2)
Here,  and
and 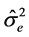 are the estimates of the corresponding variance components and are obtained either from the maximum likelihood estimation, or the one-way random effects ANOVA (Table 1).
are the estimates of the corresponding variance components and are obtained either from the maximum likelihood estimation, or the one-way random effects ANOVA (Table 1).
Using the notations, 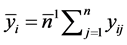 ,
, 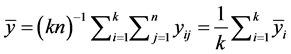 , the corrected sums of squares are given as:
, the corrected sums of squares are given as:
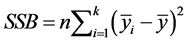 ,
,
which is the between subjects sums of squares, and , is the within subjects sum of squares. The total sum of squares is thus given by,
, is the within subjects sum of squares. The total sum of squares is thus given by,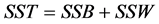 . Unbiased estimates of the variance components are given by:
. Unbiased estimates of the variance components are given by:
![]() .
.
Hence the variance components estimator of the ICC is given by:
![]() (3)
(3)
(See; Searle et al. [12] ).
With the additional assumptions of normality and independence of ![]() and
and ![]() we have:
we have:
![]()
![]() .
.
Here ![]() denotes a chi-square random variable with α degrees of freedom. Using the delta method we can derive the asymptotic bias and variance of
denotes a chi-square random variable with α degrees of freedom. Using the delta method we can derive the asymptotic bias and variance of![]() . After some simplifications we can show that:
. After some simplifications we can show that:
![]() . (4)
. (4)
Equation (4) indicates that the estimator of the ICC from the one-way ANOVA is negatively biased for all values of, n, and ρ.
Dropping the assumptions of normality regarding the distributions of bi and eij has two consequences:
1) The mean squares SB and SW will not have chi-square distributions.
2) The mean squares SB and SW are no longer independent, and hence the ratio of the mean squares will not have the usual F-distribution.
Relaxing the assumption of normality both the measures of Kurtosis of bi and eij are needed in the calculation of the asymptotic variance of ![]() and
and ![]() and the amount of bias [13] [14] .
and the amount of bias [13] [14] .
Let δe and δb denote respectively the coefficients of kurtosis of eij and bi. These quantities are defined as:
![]()
![]() .
.
Using results for the balanced one way ANOVA [14] we have:![]() ,
, ![]() and
and![]() , where
, where
![]()
![]()
![]() .
.
Using the delta method, the first order approximation for the variance of ![]() is
is
![]() .
.
Simplifying we get:
![]() . (4)
. (4)
We shall write the ![]() as
as![]() . Note that under normality
. Note that under normality![]() , and in this case the variance expression reduces to variance expression given in Donner [15] :
, and in this case the variance expression reduces to variance expression given in Donner [15] :
![]() . (5)
. (5)
Using the Taylor’s expansion for the two variables case (see Appendix I) we obtain, to the first order of approximation the asymptotic bias of the ANOVA estimator of the ICC when the assumption of normality is not satisfied as:
![]() (6)
(6)
We can then evaluate the mean square error![]() . Expressions (4) and (6) demonstrate the dependence of these quantities on the kurtosis of both the between subject and within variables. To calculate the estimated bias and variance we need not specify the complete distributions of bi and eij but good guesses for δb and δe will suffice.
. Expressions (4) and (6) demonstrate the dependence of these quantities on the kurtosis of both the between subject and within variables. To calculate the estimated bias and variance we need not specify the complete distributions of bi and eij but good guesses for δb and δe will suffice.
One question that may be stated is: which component of variation has the largest effect on the bias and variance of the reliability estimate. We answer this question empirically in two different ways. First in Table 2, we demonstrate the direct effect of the combinations of the model parameters on the bias. Subsequently, we investigate the effect of departure from normality on the sample size requirements in a typical reliability study and summarize the results in Table 2. We see from Table 2 that for selected values of the parameters combination (n, k, ρ) the smallest bias occurs when δb = δe = 0. Larger values δb increase the bias of the estimates of ICC and has more adverse effect on the bias than that caused by large values of δe. The conclusion here is that, we are worse-off by miss-specifying the distribution of the between subjects effects relative to the error term distribution. We note also from Equation (6) that δe is divided by the factor {kn} in c1, c2, and c12. The implication is that, as the number of subjects increase, the kurtosis of the error term has negligible effect on the bias and variance of the estimated reliability.
Note that the selected values for δb and δe are not arbitrary as it may seem. For example, if we assume that the error term {e} is a random variable that has a mixture of two normal distributions with ![]()
![]() and
and ![]() and a mixing proportions p1, and
and a mixing proportions p1, and![]() , we can show in general that
, we can show in general that
![]()
![]()
Table 2. Effect non-normality on bias one-way ANOVA.
![]() .
.
And a coefficient of kurtosis ![]() given by:
given by:
![]() .
.
For the case, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , the
, the![]() ,
, ![]() and the kurtosis will be 3.0625. This justifies our choice for the values of δb and δe.
and the kurtosis will be 3.0625. This justifies our choice for the values of δb and δe.
As well, non-normality has an effect on the required sample size through its influence on the variance of the estimated reliability coefficient. Suppose that we need to determine the number of subjects to detect the departure from the null hypothesis ![]() in the direction of the one-sided alternative
in the direction of the one-sided alternative![]() , with type-one error rate α and power
, with type-one error rate α and power![]() . For fixed n, we have:
. For fixed n, we have:
![]() . (7)
. (7)
If we set the Type I error rate at 5% and power at 80%, for given values of ρ0, ρ1, n, δb and δe, the estimated values of k are given in Table 3.
In this table we demonstrate the interplay between the effect size (![]() ), δb, δe, and the required sample size. Specifically, the two red-colored rows of Table 3 show that for the same effect size
), δb, δe, and the required sample size. Specifically, the two red-colored rows of Table 3 show that for the same effect size![]() , δb = 0, and δe = 6, and n = 5, we need to recruit 6 subjects (see the first red row), while for the same range of values of the reliability parameter we need to recruit 21 subjects if δb = 6, and δe = 0 (the second red row). The worst situation when the two components of variation are far from being normal. This illustrates the impact of the departure from normality of the distribution of between subjects on the sample size requirements.
, δb = 0, and δe = 6, and n = 5, we need to recruit 6 subjects (see the first red row), while for the same range of values of the reliability parameter we need to recruit 21 subjects if δb = 6, and δe = 0 (the second red row). The worst situation when the two components of variation are far from being normal. This illustrates the impact of the departure from normality of the distribution of between subjects on the sample size requirements.
![]()
Table 3. Effect of non-normality on sample size under the one-way ANOVA.
In the previous section we investigated the effect of departure from normality on the bias and the sample size requirements. In the simple case of one-way design the evaluations depend on a number of parameters. In order to extend the one-way model to the more complex model of a two-way layout, we adopt the situation when a random sample of n raters is selected from a larger population, and each judge rates each subject, that is, each judge rates k subjects. We investigate the issues of bias, mean square error (as a measure of precision of the estimated reliability parameter) and the power of hypothesis testing when the scores are not normally distributed, and when the model generating the data is that of a two-way layout. Although the extension is straight forward, we have to deal with several parameters, some of them are treated as nuisance, and others are considered essential so that we can produce useful results.
3. Bias and Variance of Estimating the Reliability under the Two-Way Random Effects Models
As summarized in the previous section, the sampling theory and formula for the standard error of the reliability estimates rely heavily on the normality assumptions, despite the fact that real data seldom satisfy these assumptions. At best we may expect that normality would be only approximately satisfied, and it does not logically follow, of course, that approximately satisfying the normality requirements guarantees automatic approximation of the actual distribution to the distribution given under normal theory. A similar problem exists for statistical inference in the two-way fixed model ANOVA, though it has been found that the distribution of the ratio of mean squares is quite robust with respect to non-normality under certain conditions [16] [17] .
The present model is the two-way mixed model ANOVA, with one observation per cell, and the primary concern is the distribution of a function of the variance component estimates, unlike the fixed model, in which the primary concern is the location parameter estimates. Thus findings in [16] cannot be generalized to reliability theory without thorough investigation. In this section we consider the model:
![]() . (8)
. (8)
The corrected sums of squares as shown in Table 4 are given as:
![]() ,
, ![]() ,
,![]() .
.
The total sum of squares:
![]() ,
,
where:
![]() ,
,![]() . Moreover,
. Moreover,![]() .
.
It is assumed that bi, rj, and eij are mutually stochastically independent with
![]() .
.
The variance of Yij is:
![]()
![]()
Table 4. The ANOVA table under the two way layout.
and the covariance between two measurements on the same subject, taken by the jth and j’th raters, is
![]() .
.
Under the above set-up, we have:
![]() ,
, ![]() and
and![]() .
.
Hence, under this model, the appropriate intraclass correlation to measure interrater reliability becomes:
![]() . (9)
. (9)
Under the assumption of normality the second, third central moments of mean squares SB, SR, and SE are given Table 5.
Define, ![]() , and
, and![]() . The ICC is thus written as:
. The ICC is thus written as:
![]() . (10)
. (10)
The variance components estimator of the ICC, using the mean squares given in Table 4 is:
![]() (11)
(11)
where![]() , and
, and![]() ,
, ![]() , and
, and![]() .
.
Note that from (10) we can write,![]() . This means that the model will have one parameter of in-
. This means that the model will have one parameter of in-
terest, ρ2, and a nuisance parameter θ2 which will be treated as fixed. Using the Taylor’s series expansion as a function of three variables, under the assumption of normality, we use the delta method and the information in Table 4 to obtain expressions for the variance and bias of ![]() and these are given in Appendix III. We noted from our calculations of the bias, variance and the MSE that:
and these are given in Appendix III. We noted from our calculations of the bias, variance and the MSE that:
1) For fixed values of θ2, k, and n, the MSE values decrease as the values of ρ2 increase. For example, when k = 20, and n = 5, θ2 = 0.1, and ρ2 = 0.7, the MSE = 0.007. While for the same set of parameters values, but ρ2 = 0.9, the MSE = 0.001. This means that the precision of the ICC estimator increases near its upper boundary. This in fact is the situation in reliability studies where high values of the ICC estimator are expected;
2) For fixed values of ρ2, k, and n, the MSE values increase (decrease in precision) as the values of θ2 increase. For example, when k = 20, and n = 5, θ2 = 0.1, and ρ2 = 0.7, the MSE = 0.007. While for the same set of parameters values, with θ2 = 0.5, the MSE = 0.009. Furthermore, when k = 20, and n = 5, θ2 = 0.9, and ρ2 = 0.7, the MSE = 0.011. The implication is that when the between rater’s variance relative to the error variance ratio increases, one should expect a loss in precision of the estimate of ICC.
![]()
Table 5. Higher moments of the corrected mean squares under the assumption of normality.
3.1. Variances and Covariance under Non-Normality
Note that in this case we need an additional coefficient of kurtosis which we denote by δr for the random effect representing raters. In his seminal paper Tukey [18] obtained the variance of the variance estimates under various ANOVA models by employing “polykays”. We modified Tukey’s results to fit our two-way random effect model. After some algebra we can show that:
![]()
![]()
![]()
![]()
![]()
![]() .
.
To investigate the effect non-normality, we again use the Taylor’s expansion to derive expression for the variance bias, and the mean square error of![]() . See Appendix VI.
. See Appendix VI.
To explore the effect of non-normality on the mean square error of![]() , we consider four scenarios, and the results are summarized in Table 6, Table 7, Table 8, and Table 9. We fixed the number of subjects, the number raters, the values of the ICC and the nuisance θ2, but we varied the kurtoses of the variance components parameters. In Table 6 we set δb = 3, δe = 0, δr = 0, in both the variance and bias terms (Appendix IV) a scenario indicating that the between subjects component of variation is not normally distributed, in Table 7 we set δb = 0, δr = 0, δe = 3, a scenario indicating that only the error term is not normally distributed, in Table 8 we set δb = 0, δe = 0, δr = 3, indicating that the between raters component of variation is not normally distributed. Table 9 summarizes the results when the three kurtosis parameters are set to zero (the normal case). The comparison among the four tables is restricted to variation in the MSE values (the last column in Table 6, Table 7, Table 8, and Table 9). We conclude that:
, we consider four scenarios, and the results are summarized in Table 6, Table 7, Table 8, and Table 9. We fixed the number of subjects, the number raters, the values of the ICC and the nuisance θ2, but we varied the kurtoses of the variance components parameters. In Table 6 we set δb = 3, δe = 0, δr = 0, in both the variance and bias terms (Appendix IV) a scenario indicating that the between subjects component of variation is not normally distributed, in Table 7 we set δb = 0, δr = 0, δe = 3, a scenario indicating that only the error term is not normally distributed, in Table 8 we set δb = 0, δe = 0, δr = 3, indicating that the between raters component of variation is not normally distributed. Table 9 summarizes the results when the three kurtosis parameters are set to zero (the normal case). The comparison among the four tables is restricted to variation in the MSE values (the last column in Table 6, Table 7, Table 8, and Table 9). We conclude that:
1) When the number of subjects is fairly large (k > 25) and for all the parameters values, the kurtosis parameter of any of the components has minor or negligible effect on the MSE.
2) For small values of ρ2 (<0.4) the bias is positive, and is negative for larger values. The variation in the nuisance parameter θ2 does affect the bias, the variance and ultimately the MSE. For small values of ρ2, the MSE decreases with increasing values of θ2, however, for large values of ρ2, the MSE increases with increasing values of θ2.
3) On comparing the MSE values in Table 6, Table 7 and Table 8 to Table 9, we find that a non-zero kurtosis δr produces the highest MSE as compared to non-zero δb. As we indicated the MSE values are smaller in the case of a non-zero kurtosis of the error term.
4. Data Analysis
In this section we analyze two data sets. Using the large sample bias and variance given in Appendix IV, we construct a Wald’s type large sample confidence:
![]() (12)
(12)
Because of the lack of exact expressions, and to assess the accuracy of the proposed approximations, we
![]()
Table 9. Bias and MSE of the ICC estimator under the normality assumption.
compare the results to the distribution free bootstrap techniques. Moreover we compare the approximate Wald’s confidence interval, in terms of width, with other proposed approximate confidence intervals proposed in the literature. To be specific we shall compare our results with:
1) Fleiss and Shrout [19] approximate confidence interval for which they applied Satterthwaite’s two-moment approximation to arrive at an approximate ![]() per cent one-sided upper bound (U) and one-sided lower bound (L).
per cent one-sided upper bound (U) and one-sided lower bound (L).
2) Capelleri JC, Ting N [20] modified the moments approximation initially proposed by Zou and McDermott [21] to obtain more accurate coverage probabilities.
3) BCa or bootstrap confidence intervals, known as the “bias corrected-bias accelerated” confidence intervals [22] [23] .
We analyze the two data sets using the R-packages [24] [25] (PSY), and (bootstrap). We provide the R-code for the first data set only since it is the same code needed for the second data set.
Example 1: Agreement among pathologists (see Figure 1).
Landis and Koch [26] evaluated the agreement among seven who classified most involved lesion of the uterine cervix. Pathologists were asked to categorize 117 using a score in the range (1 - 4): Category 1: negative, category 2: atypical squamous hyperplasia, category 3: carcinoma in situ; category 4: squamous carcinoma with early stromal invasion; category 5: invasive carcinoma. We ignored the categorical nature of the data and estimated the ICC under the model given in (8).
R-CODE
x<-Slide_2
x$Slide<-NULL
x$Serial<-NULL
head(x)
library(psy)
library(boot)
icc.c1<-function (data)
{
score <- as.matrix(na.omit(data))
n <- dim(score)[1]
p <- dim(score)[2]
data2 <- matrix(ncol = 3, nrow = p * n)
attr(score, "dim") <- c(p * n, 1)
data2[, 1] <- score
subject <- as.factor(rep(1:n, p))
rater <- as.factor(rep(1:p, each = n))
data2[, 2] <- subject
data2[, 3] <- rater
ms <- anova(lm(score ~ subject + rater))[[3]]
names(ms) <- NULL
v.s <- (ms[1] - ms[3])/p
v.r <- (ms[2] - ms[3])/n
res <- ms[3]
icc.a <- v.s/(v.s + v.r + res)
#icc.c <- v.s/(v.s + res)
return(icc.a)
}
icc.c1(x)
case.fun<-function(d,i)
icc.c1(d[i,])
icc_boot
icc_boot<-boot(x,case.fun,R=1000)
icc_boot
est<-icc_boot$t
m<-mean(est)
var(est)
sd(est)
plot(icc_boot,qdist = "norm")
boot.ci(icc_boot, type = "BCa")
Results:
Bootstrap Statistics: original bias std. error
![]()
boot.ci(icc_boot, type = "all")
Intervals:
Level Normal Basic
95% (0.5720, 0.7320) (0.5716, 0.7333)
Level Percentile BCa
95% (0.5618, 0.7235) (0.5749, 0.7320)
The ANOVA estimator ![]() has a standard error = 0.037; which is comparable to the Bootstrap standard error = 0.041. Moreover, the analytical bias in
has a standard error = 0.037; which is comparable to the Bootstrap standard error = 0.041. Moreover, the analytical bias in ![]() is −0.002, while the Bootstrap bias is −0.004.
is −0.002, while the Bootstrap bias is −0.004.
Comments:
It is clear that our proposed Wald’s 95% confidence interval is quite close to the BCa, and this is attributed to the large sample size. Moreover, we can see from the histogram, and the q-q plot of the bootstrap samples of t*, as shown in Figure 1, which is in fact![]() , that it has a symmetric normal distribution even though we are certain that the original scores are not normal.
, that it has a symmetric normal distribution even though we are certain that the original scores are not normal.
Example 2: Grading of retinopathy (see Figure 2).
Retinopathy score of retinal whole mounts was performed using fluorescent microscopy, and images were acquired using a digital camera. The extent of retinal neovascularization (NV) was estimated by implementing a specific retinal NV scoring system. In brief, the entire retina was outlined to distinguish the total retinal area of each eye. Then, the images were given threshold to emphasize only the FITC-perfused vessels. This permitted the measurement of total blood vessel area of each retina and the percentage of each retina that is engrossed with blood vessels. The scoring system was based on selecting several criteria, these are; 1) the size of the central avascular area, 2) blood vessel tuft formation, 3) extra-retinal neovascularization and 4) presence of blood vessel tortuosity. For the purposes of this model, we divided the retina into three areas: zone 1, the inner circumferential third of the retina around the optic disc; zone 2, the middle third of the retina; and zone 3, the outer third of the retina. The extent of disease was specified by clock hours or distance around the retina (number of twelfths similar to a clock). The scoring was performed in a masked fashion, by employing fluorescence microscopy, evaluating and scoring each retina in a blinded manner by three observers. The minimum score according to this method is 0, and the maximum score is 13. Maximal vaso-proliferation in this mouse model has previously been reported to occur from P17 to P21. The average retinopathy score for each animal was used for statistical analysis [27] .
![]()
Figure 1. Graphs of histogram and q-q plot of the 1000 bootstrap sample for example 1.
Bootstrap Statistics: original bias std. error
![]()
The ANOVA estimator is 0.958, with standard error = 0.019. The analytic bias is −0.006, but the Bootstrap bias is −0.005.
Comments:
Although the sample here is much smaller (k = 16) the Wald’s 95% confidence interval is quite close to the corresponding bootstrap confidence interval. But the distribution of ![]() is far from being normally distributed as can be seen from the histogram (skewed to the left) and the curved q-q plot in Figure 2.
is far from being normally distributed as can be seen from the histogram (skewed to the left) and the curved q-q plot in Figure 2.
For example 1, Table 10 gives the ANOVA results, and Table 11 gives the 95% CI for the 6 methods. For example 2, Table 12 gives the ANOVA results, and Table 13 gives the 95% CI for the 6 methods.
![]()
Figure 2. Graphs of histogram and q-q plot of the 1000 bootstrap sample for example 2.
![]()
Table 10. ANOVA table for the first data set.
![]()
Table 11. Comparing 95% CI by alternative methods.
![]()
Table 12. ANOVA table for data of example 2.
![]()
Table 13. Comparing 95% confidence intervals by different methods for data of example 2.
5. Discussion
The use of the intraclass correlation to assess the reliability of judgments made by the observers is ubiquitous in medical research. Unreliable measurements can eventually affect the diagnosis of diseases and hence expose patients to undesired health risks. Several examples regarding the applications can be found in [2] [3] [5] .
1) In the one-way we observe that from the tables that the effect of normality on the variance and the bias of the estimated ICC depend on the kurtosis of the distributions of the components of variation. We noted that the kurtosis of the between subjects component of variation is multiplied by the factor k−1, kurtosis of the between rater’s component of variation is multiplied by a factor n−1 and that of the error component multiplied by a factor![]() . Therefore the effect of non-normality of the between raters component will dominate that of the subjects component would dominate the effect of non-normality of the error (within subjects) components. In general, non-zero kurtosis of the observed distribution of measurements substantially affects the sampling distribution, the bias, and standard error of reliability estimates. For the two-way model, there is an interaction between the values of ρ and the nuisance parameter (ratio of between subjects variance to the error variance).
. Therefore the effect of non-normality of the between raters component will dominate that of the subjects component would dominate the effect of non-normality of the error (within subjects) components. In general, non-zero kurtosis of the observed distribution of measurements substantially affects the sampling distribution, the bias, and standard error of reliability estimates. For the two-way model, there is an interaction between the values of ρ and the nuisance parameter (ratio of between subjects variance to the error variance).
2) The magnitude of ρ has an effect on the sampling distribution of the reliability estimate. The larger the value of ρ the smaller the mean square error of its estimator. This observation is relevant within the framework of reliability studies since we are interested in producing large values of the estimate.
6. Summary
From the above discussion we summarize our conclusions in three points:
Firstly, the effect of non-normality of the scores distribution is not tangible for k > 25 (fairly large), where k is the number subjects. Secondly, large value of reliability, which is our main concern, has smaller variance, and hence a Wald’s confidence interval on the population ICC would be acceptable. This conclusion is based on the empirical evidence; as we have shown that the Wald’s interval is almost identical in length to the interval based on the bootstrap methods. Thirdly, in the design stage of a reliability study a reasonable guess of the kurtosis is required to satisfy, for given effect size and type I error rate, the sample size requirements to achieve a certain power on specific hypotheses.
We should also note that the estimation problem in the two-way model can be more complex particularly when the raters are required to repeat the assessment of each patient, in order to reduce bias and increase precision of the reliability estimator. In this case the sample size question can be: what is the number of subjects, the number of raters, and the number of repeats per subjects to achieve certain power level. In such case one has to seriously consider the cost of replications in the early stages of designing reliability study.
Appendices
Appendix I: The Taylor’s expansion of a function of several variables.
Let ![]() be a random vector with
be a random vector with ![]() be a real valued continuously differentiable function of X.
be a real valued continuously differentiable function of X.
The Taylor series expansion of ![]() around
around ![]() is given by:
is given by:
![]()
Appendix II: Analytic formula of the bias of the estimated intraclass correlation under the one-way random effects model.
1) The non-normal case:
![]()
2) Under normality ![]()
![]() . Hence
. Hence
![]()
Appendix III: Analytic expression for variance and bias of the estimated intraclass correlation in the two- way random effects model:
1) Variance Expression under normality:
![]()
It would be most informative to express the bias and variance in terms of ρ (the primary parameter of interest) and simplify the expressions accordingly:
![]()
We can now write variance expression as
![]()
![]()
![]()
where, ![]() , and
, and ![]()
2) Bias in Estimating ![]() under normality.
under normality.
A first order approximation of the bias under the assumption of normality is given by:
![]()
The terms of the bias expression are:
![]()
![]()
and
![]()
Appendix IV: variance and bias of estimated intraclass correlation under non-normality.
Variance:
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
where ![]()
Bias:
The delta method is used to derive the variance of ![]()
![]()
![]()
where ![]()
![]()
![]()
![]()
![]()
![]()
![]()