Received 3 March 2016; accepted 19 April 2016; published 22 April 2016
1. Introduction
Since Mankiw and Whinston (1986) [1] established the excess entry theorem to reveal that entry is socially excessive to the oligopolistic market where homogeneous final goods are produced in a Cournot fashion by identical firms with economies of scale due to the existence of fixed costs, numerous attempts have been made to examine the robustness of that theorem by paying attention to various aspects that were assumed away in the original excess entry model, such as spatial competition (Matsumura and Okamura (2006) [2] ), market power of producers (Ghosh and Morita (2007) [3] [4] ), external economies of scale (Mukherjee (2010) [5] ), market leadership (Mukherjee (2012) [6] ), R&D tournament (Mukherjee and Wang (2011) [7] ), and product differentiation (Kagitani, Ohkawa and Okamura (2015) [8] ).
Although these studies successfully extended the excess entry theorem, little attention has been paid to the fixed costs, which is one of the main sources to generate the theorem. In the present paper, formulating the fixed costs as irreversible investment under uncertainty, as well as inspired by Youn and Tremblay (2015) [9] that introduced Brownian motion to reveal new properties of oligopolistic market, we attempt to demonstrate another aspect of the excess entry theorem. More precisely, we formulate the Cournot model by making use of the optimal stopping theory that has been used to determine the optimal timing in stochastic economies since McDonald and Siegel (1986) [10] demonstrated the value of waiting, followed by Dixit (1989) [11] that examined the optimal timing of entering foreign market, Farzin, Huisman and Kort (1988) [12] that investigated the optimal timing of IT investment, Bentolila and Bertola (1990) [13] that considered the optimal timing of employment/ lay-off, Fujita (2016) [14] that showed the effect of increase in uncertainty and number of entrants on firm’s optimal timing of investment and so on.
The most related work is Fujita’s (2008) [15] that constructed a stochastic model where firms are heterogeneous and number of the entrants determines endogenously, to show that growth rate of welfare increases as number of the entrants decreases over time. In the present paper, contrary to Fujita (2008) [15] , we assume that firms are identical and number of the entrants is exogenous as in the original model of the excess entry theorem.
It is revealed that free entry in a stochastic oligopolistic market is socially excessive, owing not only to the presence of scale economies but also to the value of waiting. That is, if number of the entrants is large, the value of waiting increases so as to postpone the entry and decrease sum of discounted values of the welfare. It is also shown that welfare maximizing number of entrants is larger if the market is more uncertain.
Structure of this paper is as follows. After laying out a basic model to derive the Cournot equilibrium in Section 2, Section 3 determines the optimal timing of the entry of each firm. Based on these analyses, in Section 4 we demonstrate stochastic version of the excess entry theorem. Concluding remarks are made in Section 5.
2. Basic Model
Let us consider a stochastic oligopolistic market where time passes continuously with importance of the future diminishing with discount rate ρ and there exist n identical firms that engage in two stage game, where each firm determines timing of the entry in the first stage, followed by the second stage that determines the Cournot equilibrium in each period. Let us assume each firm incurs entry cost of K and has a constant marginal cost of c.
Letting xi(t) and p(t) denote the ith firm’s output and the unit price of the product in period t, respectively, we
assume p(t) is related to the total output in period t, 
, through the following linear inverse de-
mand function,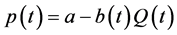 
, where a is a positive constant that indicates the choke price, while b(t) is a positive variable that represents the size of the market in period t, which we assume to fluctuate stochastically according as the following geometric Brownian motion as in Fujita (2016) [14] ,
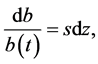(1)
with initial value b0, where s is a positive constant that expresses volatility in a sense that larger s means more uncertain expansion of the market, while dz is Wiener process that expresses the random movement.
Following the standard procedure of the backward induction, let us first derive the equilibrium in the second stage, i.e., the Cournot equilibriumin each period after the entry. Since the ith firm’s profit in period t, πi(t), is
described as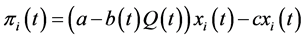
, we have the ith firm’s first order condition for the profit
maximization as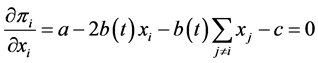 
for every
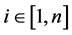, to yield the ith firm’s output and
profit in the Cournot equilibrium in period t, respectively, as
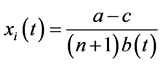; (2)
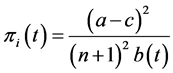. (3)
Since we have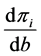 
and 
from Equation (3) as 
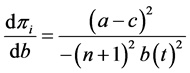and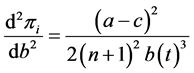
,
we can express the stochastic process of the ith firm’s profit by making use of Ito’s lemma as
(4)
with initial value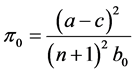
, where μ = s2 and σ = −s.
3. Optimal Timing of Entry of Each Firm
Next, let us determine the ith firm’s optimal timing of the entry in the first stage.
For this purpose, as a preliminary, let G(π0) denote the expected value of one unit of the ith firm’s profit at the period of its entry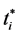 
(i.e., the expected value of![]()
) as a function of the initial profit π0. Then, the general solution to G(π0) is expressed as
![]()
, (5)
where γ1 < 0 and γ2 > 0 are solutions to the characteristic equation![]()
, which is rewritten as ![]()
by substituting μ = s2 and σ = −s into it. If we let ![]()
denote the ith firm’s profit in period![]()
, it follows that α = 0 and ![]()
since G(π0) satisfies ![]()
and![]()
, which combined with Equation (5) yields![]()
. Letting γ denote γ2, we obtain
![]()
(6)
where
![]()
. (7)
Thus, we can calculate the ith firm’s object function ![]()
to maximize in period 0 as
![]()
. (8)
Now, if we let ![]()
denote the market size b in period![]()
, the ith firm’s profit in the Cournot equilibrium is ex-
pressed as![]()
, which together with Equation (8) yields the ith firm’s sum of discounted values of
the profits in each period after the entry in the following way as a function of![]()
,
![]()
. (9)
So that, by differentiating Vi with respect to ![]()
and assuming symmetric solution also for the timing of the entry, i.e., ![]()
for every![]()
, we have the optimal cut off level of the market size b for each firm as
![]()
. (10)
Note that the optimal timing is expressed by the cut off level of the market size b, since the model of the present paper is stochastic.
Since small b* in the present model means postponement of the entry and b* is a decreasing function of n as Equation (10) shows, the following lemma is derived.
Lemma: Entry of each firm is postponed as number of the entrants increases.
4. Other Aspects of Excess Entry Theorem
Now, we are ready to describe the equilibrium sum of discounted values of the welfare in each period after each firm’s entry.
Firstly, by substituting ![]()
and Equation (10) into Equation (9), we have the ith firm’s equili-
brium sum of the discounted profits in each period after the entry as
![]()
. (11)
Similarly, if we let cs(t) denote consumers’ surplus in period t, sum of discounted values of the consumers’ sur-
plus in each period after each firm’s entry t*, ![]()
, is obtained as![]()
, which together with the consumers’ surplus in period t, ![]()
, yields the equilibrium sum of discounted values of
the consumers’ surplus in each period after each firm’s entry t* as
![]()
. (12)
Thus, by substituting Equation (11) and Equation (12) into sum of the discounted welfares in each period after
each firm’s entry t*, ![]()
, we have the equilibrium sum of
discounted values of the welfare in each period after each firm’s entry t* as
![]()
. (13)
Since γ is greater than 1, graph of W is depicted on n-W space as a hump-shaped trajectory as in Figure 1,
![]()
Figure 1. Relationship between number of entrants and the welfare.
which is in sharp contrast with the Cournot limit theorem that shows that the welfare increases monotonically as number of the entrants increases.
To be exact, by differentiating W with respect to n and setting it to zero, we have the optimal number of the entrants nB as
![]()
. (14)
Since Vi converges to zero as number of the entrants increases as Equation (11) shows, number of the entrants at the free entry level is infinity. Thus, this hump-shaped trajectory indicates that the welfare maximizing number of the entrants is less than the number of the entrants at the free entry level, which is consistent with the excess entry theorem.
We can explain the cause of excessive market entry as well as its impact on the market, which is peculiar to the present paper, in the following way.
First of all, in the original model of the excess entry theorem, consumers’ surplus goes up as number of the entrants increases. Such increase in the number of entrants also increases sum of firms’ fixed costs, which contributes to reduction of the welfare. In this way, increase in the number of entrants has two effects on the welfare, i.e., pulling up consumers’ surplus and reducing firms’ surplus, which determines the optimal number of firms to balance these two effects.
In a stochastic market of the present paper also, as in the original model of the excess entry theorem, consumers’ surplus rises in accordance with increase in the number of the entrants. There is, however, another factor that affects the welfare and the optimal number of firms, i.e., the value of waiting that is generated by increase in the number of the entrants. That is, increase in the number of the entrants postpones the timing of the entry as the above lemma shows, to reduce sum of discounted values of the consumers’ surplus. Thus, we can derive the following proposition 1, which can be called a stochastic version of the excess entry theorem.
Proposition 1: Free entry in a stochastic oligopolistic market is socially excessive, owing not only to the presence of scale economies but also to the value of waiting.
As is clear from Equation (14), nB increases if γ decreases, while Equation (7) shows that γ decreases in accordance with increase in s. Since increase in s means increase in the volatility, we have the following proposition 2.
Proposition 2: Welfare maximizing number of the entrants is larger if the market is more uncertain.
As Equation (4) shows, increase in the market volatility s raises the growth rate of each firm’s profit, which also strengthen the market power of each firm. Proposition 2 shows that more competition is necessary in order to prevent such market powers from increasing.
5. Concluding Remarks
By reformulating the Cournot model by making use of the optimal stopping theory, the present paper attempted to demonstrate other aspects of the excess entry theorem.
It was revealed that: 1) free entry in a stochastic oligopolistic market is socially excessive, owing not only to the presence of scale economies but also to the value of waiting; 2) welfare maximizing number of the entrants is larger if the market is more uncertain.
There are two prevailing beliefs on the relation between competition and welfare. One belief is that competition increases welfare, while the other belief is that competition is destructive. Indeed, competition occupies so important a position in economics that it is difficult to imagine economics as a social discipline without it as Demsetz (1962) [16] pointed out. The present paper attempted to shed new light on this issue by paying attention to fixed costs that are required to enter the market.
It is necessary to relax the assumption of geometric Brownian motion, as well as to give an empirical testing of this model, in order to contribute to the advancement of the studies on the excess entry theorem. It is also necessary to examine the robustness of the results by paying attention to spatial competition, market power of producers and so on. These are issues which are left for our future research.