Development of the Orbital-Free Density Functional Approach: The Problem of Angles between Covalent Bonds ()
Received 4 January 2016; accepted 25 March 2016; published 28 March 2016

1. Introduction
A number of works (for instance [1] - [9] ) devoted to development of the orbital-free (OF) version of the density functional theory (DFT) [10] [11] appeared last years. This approach, in contrary to the Kohn-Sham (KS) method, does not use the wave functions (orbitals) and operates with the only electron density. The OF approach is a consecutive development of the idea of Hohenberg-Kohn [11] that the basic state of a quantum system can be completely described by means of electronic density.
There is a significant progress in modeling of two-atomic systems [3] [8] and even simple crystals [12] . However, even now there is a big unsolved problem interfering further development of the OF approach. This problem concerns description of the angular dependence of the interatomic bonding in systems with covalent bonds. As we know, till now there are no works where this problem is solved awfully.
An essential trouble is the fact that the electronic density of a single (isolated) atom is spherical, i.e. the “orbital-free” atom has a shape of a ball, but balls form the close packed structures. For example, three identical atoms are obliged to form an equilateral triangle with corners of 60 degrees. At the same time, it is known that three atoms of silicon form an isosceles triangle with the main corner of about 80 degrees [13] , atoms of carbon build a linear chain [14] , and atoms of aluminum really behave like balls―they form a correct equilateral triangle [15] . Obviously, if an approach can describe the angular properties of trimers, it can solve the same problem for more complicated atomic systems too.
In our recent papers [16] [17] , we have showed how it is possible, using single-atoms calculations by the Kohn-Sham DFT method (KS-DFT), to find the kinetic functions for single atoms and to use them for orbital-free modeling of atomic dimers. The present work is an attempt to develop (on example of Al, Si, and C trimers) a technique which would allow to describe an adequate geometry of interatomic bonds in polyatomic systems in the framework of the OF approach.
2. A Principal Point and Results
As in our recent works we used here the pseudopotential approach with the FHI98pp package [18] as a generator of pseudo-potentials and equilibrium partial electron densities for single atoms. The general way of calculations is the same as described in [18] . Studied atoms were located in a cubic cell of the L size (L = 52 a.u.; 1 a.u. = 0.529 Å). The cell was divided on 128 × 128 × 128 elementary sub-cells for the integration with the step ΔL of 0.406 a.u. Results of calculations were compared with published data.
Transfer from dimers to trimers is a principal point because trimers characterized by some angles between atomic bonds.
To describe the angular dependence of interatomic bonding in the framework of the OF approach we must analyze the reasons of this dependence in the standard quantum-mechanical approach, which uses wave functions and electronic states. For example, it is specified in the work [19] that the angular peculiarities of a cluster Si3 are defined by the Yang-Teller effect caused by existence of the energy gap between occupied and empty states. In other words, the difference of structures of semiconductor and metal small clusters is connected with the difference of their electronic states and bond wave functions. Namely, covalent atoms have full occupied bonding states corresponded to localized functions orientated between nearest atoms; these states are separated by the energy gap from above lied non-occupied states. Metallic atoms have dispersed functions without orientation in the space and without energy gaps between them.
In our case wave functions are absent, electronic states are absent too, and, therefore, we cannot speak about any energy gap. In the OF approach we deal only with the electronic density which defines all energy and structure of the polyatomic system. However the main quantum-mechanical rules remain fair and in this case. We have not to forget that quantum mechanics is not only a set of wave functions and electron states. We have not to forget the Paulie’s principle specifying that in one quantum state there can be only two electrons (without taking into account a spin). In our case this principle may be paraphrased by a following way: a covalent bond is formed by two electrons, the common wave function of which is localized in the space between two nearest atoms. It is obvious that the quantity of the electrons which are responsible for this bond doesn’t change as the distance between atoms changes (if, of course, the bond isn’t broken at all and the electronic structure isn’t reconstructed completely). In case of the metals the states are close each other and electrons can easily “flow” from one state to another during the changing of the atomic geometry.
The above mentions may be reformulated in the language of the electronic density: the density integral (nint) between atoms with covalent bonding, has to remain its value at change of distance between atoms; in case of metal bonding the value of the integral nint can be any possible. Certainly, there is a question: on what space we have to provide integration? And what have we to do with intermediate cases, with atoms of different types? We will leave these questions for the future, and now we will try to explain the difference in structure of covalent and metal systems on the example of homogeneous clusters Al3, Si3 and C3.
It is obvious that the space of integration has to be rather local and at the same time it has to give us the information on quantity of the electrons included in a covalent bond. In the present work we used the space having a shape of the slab situated between two nearest atoms (Figure 1) and oriented perpendicularly to the plane in which the trimer triangle is placed. Thickness of a slab was taken of 2ΔL, but for some test calculations we used slabs of 4ΔL and 8ΔL thickness. As the number of the integration points can be changed at change of the trimer configuration, the value of nint was normalized to one point.
![]()
Figure 1. The scheme of an arrangement of atoms in a trimer. Dashed lines show the space on which the electronic density is integrated for definition the number of the electrons involved in the covalent bond; α is a corner between bonds with identical lengths of d.
As it was said above the integral of electron density between the nearest atoms is the critical parameter for covalent bonding. It cannot be larger than some value that is a characteristic of a so called saturated bond. Let us
take the interatomic bond in a dimer as a standard saturated bond. Let us call the value 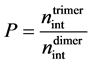 (the relation
(the relation
of nint of a trimer to nint of a dimer) as “the bonding strength” and accept that for covalent bonds the value of P shouldn’t exceed 1.0 at change of the distance between atoms. For metallic bonds the value of P can be any possible.
Calculated values P for clusters Al3, Si3, and C3 are presented in Figure 2 as functions of the angle between interatomic bonds in the case when restrictions on these values are absent. For each angle we found the values of interatomic distances, which corresponded to the minimum of the total energy of the cluster. One can see that P is equal approximately 1.0 at α = 180˚ and increases when α approaches to 60˚. The maximum value (P = 1.40) is observed for carbon, that has the smallest interatomic distances. Interatomic distances in aluminum and silicon are approximately the same, therefore no wonder, as the “bonding strengths” for the Al3 and Si3 trimers are approximately equal.
In order to check reliability of our results we repeated the calculations using thicker slabs (4ΔL and 8ΔL) for integration of values nint (dimer) and nint (trimer) between atoms in dimers and trimers and we found that results have changed no more than by 2 per cent.
In Figure 3 (curve A) we present results of calculations of binding energy for the Al3, Si3 and C3 trimers without restriction of the “bonding strengths”. From these curves it is clear that in all three cases the minimums of the binding energy correspond to triangular clusters, “bonding strengths “in which significantly exceed the corresponding values, characteristic for linear chains. This result looks natural for aluminum as its states have the metallic, not localized character; but for the clusters of Si3 and C3 having covalent bonds it is necessary to introduce the restrictions on values of P stipulated above. We have taken into account this condition (P = 1) and found dependences of the binding energy on the angle between bonds in the Si3 and C3 clusters (Figure 3, curve B). One can see that atoms of carbon seek to form linear chains, while for silicon neither a linear chain, nor an equilateral triangle is energetically favorable: atoms of silicon prefer to form an isosceles triangle with the angle α of 80 degrees.
Equilibrium values of interatomic distances d, angles α, and binding energies Eb (absolute values) for the trimers Al3, Si3, and C3 are collected in Table 1 (calculated for the condition P = 1) in comparison with known data. One can see that comparison is good. Thus, we showed that orbital-free approach is capable to describe correctly orientations of interatomic bonds in atomic clusters, as well as values of interatomic distances and binding energies.
It is interesting to compare our results for interatomic densities with results of standard KS-DFT calculations. For this purpose we calculated “bonding strengths” P for Si3 and Al3 using the popular KS-DFT code FHI96md [28] for the same triangles as were studied above. We have found that P was equal 1.0 (±0.02) for all cases for Si3, but it increased up to 1.3 for the Al3 equilateral triangle. These results are in excellent agreement with our OF ones.
3. Conclusions
We showed that the use of the restriction principle for the interatomic density (following from the Paulie’s
![]()
Figure 2. “The bonding strengths” in the Al3, Si3 and C3 trimers as functions of the corner between interatomic bonds in the case when restrictions on the interatomic electron density is absent.
![]()
Figure 3. Calculated dependence of binding energy (on atom) for the Al3, Si3 and C3 trimers on the angle between interatomic bonds. A) Values are obtained without restrictions on electronic density in interatomic bonds; B) Values calculated with the condition P = 1.0.
![]()
Table 1. Equilibrium distances d, angles α and binding energies Eb (absolute values, per atom) for Si3, Al3 and C3 in comparison with known calculated data.
Notations: a [13] , b [20] , c [21] , d [22] , e [23] , f [24] , g [15] , h [25] , i [14] , j [26] , k [27] .
principle) allowed us to describe correctly angular dependences of the interatomic bonding in polyatomic clusters in the framework of the orbital-free version of the density functional theory. In particular, it is possible to show that for the Al3 cluster, the equilateral triangle is favorable; the Si3 trimer is characterized by the isosceles triangle with angles of 80 and 50 degrees, and three atoms of carbon built the linear chain. Calculated equilibrium interatomic distances and the values of binding energy are well compared with the known data.
As the problem of the correct description of angles between interatomic bonds is a key point in modeling of polyatomic systems, it is possible to consider that our work opens a direct way to design an effective method of modeling of big nanosystems and supermolecules.
We have to note that the consideration which is carried out above is directly applicable only to the systems consisting of identical atoms and requires a special development for application to more complicated systems.