Attenuated Model of Pricing Credit Default Swap under the Fractional Brownian Motion Environment

Wenjing Gu¹, Yinglin Liu², Ruili Hao^3*

¹School of Mathematics, Shanghai University of Finance and Economics, Shanghai, China.
²Faculty of Business and Economics, Macquarie University, Sydney, Australia.
³Department of Financial Mathematics, Shanghai Finance University, Shanghai, China.

DOI: 10.4236/jmf.2016.62021                

Abstract

This paper mainly discusses the pricing of credit default swap (CDS) in the fractional dimension environment. We assume that the default intensity of a firm depends on the default states of counterparty firms and the term structure of interest rates, but the contagious impact of the counterparty firm is decreasing over time, until disappears. The interest rate risk is reflected by the fractional Vasicek interest rate model. We model the firm’s default intensity in the looping default framework and derive the pricing formulas of risky bonds and credit default swap.

Keywords

Credit Default Swap, Fractional Brownian Motion, Contagious Risk, Hyperbolic Attenuation Effect, Looping Default

Received 11 January 2016; accepted 6 March 2016; published 9 March 2016

1. Introduction

Credit default swap was one of the most important derivatives in the financial market, which was created by JP Morgan in 1995 to manage credit risk. Credit default swap (CDS) is a kind of bilateral agreements. Because it was easy to implement standardization which was firstly founded by the ISDA (the international swaps and derivatives association) in 1998, the credit default swap market had the rapid expansion. However, some con- cealed contradictions exposed gradually, such as the United States subprime crisis and the European sovereign debt crisis. They make people realize that credit derivatives bring convenience and contain huge risk at the same time, especially contagious risk. Therefore, the pricing problem of credit default swap became a hot research topic in recent years.

Until now, there have been mainly two basic CDS’s pricing models: the structural model and the reduced- form model. Structured model was firstly built by [1] based on the basis of Black-Scholes option pricing theory. In this model, the firm’s default is governed by the value of its assets and debts. However, the information of the firm’s assets is usually unknown while the default in the reduced-form model is governed by the exogenous factor. The information of the firm’s assets is usually unknown and the problem of the valuation of credit de- rivatives involving the jump-diffusion process is still difficult to get explicit results in the event of defaulting before the maturity date in the structural model. Therefore, comparing with the structural approach, the reduced- form approach is more flexible and tractable in the real market. In this paper, we will price the bonds and CDS in the reduced-form models.

Reduced model contains intensity model and non-intensity model. The intensity model was pioneered by by [2] and [3] . They introduced exogenous mechanism to describe the firm’s default. Their models considered the default as a random event which was controlled by an exogenous intensity process. With the more aggregate credit risk in the modern financial markets, we have recognized that the defaults of many firms have direct linkage. Thereby the valuation of credit securities with contagious risk has aroused a lot of authors’ interests.

[4] firstly proposed the model of credit contagion to account for concentration risk in large portfolios of defaultable securities (DL Model). Later, motivated by a series of events such as the South Korean banking crisis, Long Term Capital Management’s potential default and so on, [5] thought the traditionally structural and reduced-form models were full of problems because they all ignored the firm’s specific source of credit risk. They generalized the Davis’s contagion model and introduced the concept of counterparty risk which was from the default of firm’s counterparties. [6] gave the analytic expression of CDS premium by using the change of measure introduced in [7] . Because it was impossible to assume that the impact of one firm’s default to another firm’ default kept constant all the time, [8] introduced a hyperbolic function to reflect the attenuation effect and generalized the model in [6] .

Recently, [9] and [10] considered the jump-diffusion risk of the interest rate and discussed the pricing problem of CDS in the contagious model. In fact, the interest rates in the real financial market show the properties of self-similarity and long-range dependence. However, the interest rates in above papers are all driven by standard Brownian motion which dose not reflect these properties. Therefore, [11] used the fractional Brownian Motion to describe the interest rate and studied the pricing of the bond and CDS with the contagious risk under the fractional Vasicek interest rate model. But they did not consider the case that the contagious effect decreased with time. Based on the previous studies, this paper will establish the attenuation model of the contagious risk and deduce the pricing formula of credit default swap in the fractional dimension environment.

2. Preliminaries

As the fractional Brownian motion has the properties of self-similarity and long-range dependence and many phenomena in financial market show these properties in some certain, the fractional Brownian motion becomes a very suitable tool in different applications such as mathematical finance. The fractal Brownian motion was introduced by Kolmogorov in Hilbert space. This paper also consider the Hurst index. We will give the following definitions and theorems without the proofs. The details can be found in [12] .

Definition 1. Let 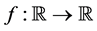be measurable. Then if

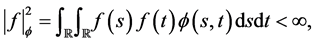
where,.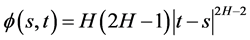

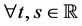Definition 2. (Fractional Brownian motion) Let be the filtered probability space satisfying the usual conditions. 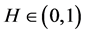is a constant. The fractional Brownian motion with Hurst index H is a continuous Gauss process, which satisfies

1);

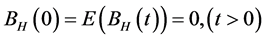2).

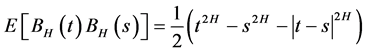Definition 3. (Quasi-conditional expectation) Let, 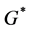is the random distribution space with inductive topology, then the quasi-conditional expectation of G with respect to 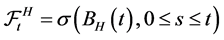is defined by

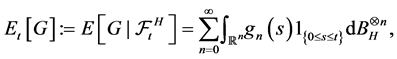(1)

where. For simplicity, we denote it as.

Definition 4. (Quasi-martingale) Suppose that is an adapted stochastic process with respect to. If, then we say that is a quasi-martingale.

From the above definitions, it is easy to prove the following theorems:

Theorem 1. ( [12] )

1) is a quasi-martingale;

2) Let, then is a quasi-martingale;

3) Let, then is a quasi-martingale.

The interest rate has an important influence on pricing credit derivatives, especially after the fixed interest rate is replaced by the floating interest rate, the impact will be more important. From the point of time, the interest rate also has the characteristics of the fractional Brownian motion. Therefore, [13] used the fractional Brownian motion to describe the interest rate process which was the fractional Vasicek interest rate model and priced the European option. In this paper, we also consider the Vasicek interest rate model:

(2)

where is the fractional Brownian motion which describes the market risk, is the standard deviation which represents the stochastic volatility, parameter b is the long-term average of interest rate, a represents the speed of recovery that returns to b from the deviation value of the long-term average. The interest rate has the following explicit solution:

(3)

where is the interest rate value at time 0. follows the normal probability distribution with mean 0 and the variance. Thus, is the normal stochastic variable with mean and the variance.

To make the formula simple, we suppose that the face value of bond is 1 dollar. The default-free bond’s price was obtained in [13] as following:

Theorem 2. ( [13] ) Let is the time-t value of the default-free bond with the maturity date T. The interest rate is derived by the fractional Brownian motion as

(4)

where a, b and are constant, is Standard Brownian motion, the price of market risk is, then

(5)

where

The above conclusions were all obtained by using the classical theory of the fractional Brownian motion in ref. [14] and [15] .

3. Attenuation Model of Bonds’ Pricing in Looping Default Framework

Suppose that is a filtered probability space satisfying the usual conditions, where (is large enough but finite) and is the fractional Brownian motion on. is the -field that generated by and P is an equivalent Quasi-martingale measure on. There is a -valued process where X represents the economy- wide state variable. Denote and, where repre- sents the default process of company i. When first jumps from 0 to 1, we call the company i defaults and denote be the default time of company i. Thus, where is the indicator function.

As is generated by the economic state variables and the default process of m firms

(6)

where and are generated by and respectively.

Denote

(7)

(8)

This paper consider that the interest rate is the only state variable and is the default intensity of that adapted to, where. The default times of company i can be defined as

(9)

where is the unit exponential random variable. The conditional and unconditional default probability distributions of company i is given respectively by

(10)

and

(11)

In the following, we consider the simple case with two firms: firm A and firm B. Their defaults are mutually influenced and both correlated with the market interest rate. We assume that their default intensity satisfy the below relations respectively:

(12)

where, are real, and,.

We will give the defaultable bond’s price without the proof (see [5] ). Let

Lemma 1. ( [5] ) Suppose that the bond issued by firm i has the maturity date T and the recovery rate. Let the default time be, the default intensity be and the interest rate be, then

(13)

Now, we calculate the conditionally marginal distributions of default time and in [0, T] before deriving the prices of bonds. To avoid the looping influences, we firstly apply the change of measure to get the joint conditional distributions of and. We define two firm-specific probability measures by

(14)

Under the new measure, the intensity () for.

Thus, the default model can be simplified and the calculation of the default probabilities and bonds’ prices will be relatively easy.

Theorem 3. Let and be the default times of firm A and B. Assume the interest rate follows the Vasicek interest rate model (2) and the default intensities, satisfy attenuation model (12). If no

defaults occur up to time t, then the joint conditional distribution of and on is given by the following,when, then

(15)

when, and

(16)

The proof can be found in the Appendix.

Corollary 1. Let and be the default times of firm A and B. Suppose that the default intensities and satisfy attenuation model (12). If no defaults occur up to time t, then the conditionally marginal dis- tributions of and on are given by

(17)

(18)

Proof. We can obtain the corollary from Theorem 3, so omit the process.

Now, we apply the above results to price the bonds issued by firm A and B in the looping default framework. We firstly give the other form of pricing formula for the bond. Later, we will price the bonds based on this formula.

Lemma 2. ( [5] ) The defaultable bond price can also be expressed as

(19)

In this paper, we will not consider the risk from the recovery rate. Therefore, without loss of generality, we suppose that the recovery rates and the face value of bond is 1 dollar.

Theorem 4. Assume the interest rate follows the Vasicek interest rate model (2) and the default in- tensities, satisfy attenuation model (12). If no defaults occur up to time t, then the time-t prices of bonds issued by firm A, B with the same maturity date T are respectively given by

(20)

(21)

where

where

The proof can be found in the Appendix.

4. CDS’s Pricing

In this section, we apply the results in section 3 to price CDS related to the zero coupon bond issued by firm A. Firm C holds a bond issued by the reference firm A with the maturity date T. To seek protection against the possible loss, firm C buys a default swap with the maturity date from firm B on condition that firm C gives the payments to seller B at a fixed swap rate in time while seller B promises to compensate buyer C for the loss caused by the default of firm A at a certain rate. Each party has the obligation to make payments until its own default. The source of credit risk may be from three parties: the issuer of bond, the buyer of CDS and the seller of CDS.

In the following, we discuss a simple situation which only contains the default risk from reference firm A and the CDS’s seller B. At the same time, to make the calculation convenient, we suppose the recovery rate of the bond issued by firm A is zero and the notional is 1 dollar. In the event of firm A’s default, firm B compensates firm C for 1 dollar if he doesn’t default, otherwise 0 dollar.

Now, we give some notations. Denoted the swap rate by a constant c and interest rate by. Let the default times of firm A and B be with the intensity and with the intensity respectively. We analyze the values of two legs: contingent leg and premium leg. The time-0 market value of buyer C’s payments to seller B is

the time-0 market value of firm B’s promised payoff in case of firm A’s default is

Then, in accordance with the arbitrage-free principle, we obtain

(22)

Theorem 5. Suppose the interest rate follows the Vasicek interest rate model (2) and the default in- tensities, satisfy attenuation model (12). Then, if no defaults occur up to time t, the swap rate C has the following expression

(23)

where

(24)

(25)

and, are the simple forms of (21) and (20) in Theorem 4.

Proof.

(26)

To derive the swap rate of CDS in the looping default framework, we define a firm-specific probability measure by

then

(27)

Substituting the quasi-conditional expectation into the above formula of the swap rate C, we deduce (40).

5. Conclusions

This paper studies the pricing of the defaultable bonds and credit default swap when contagious risk has the attenuation effect in the fractional dimension environment. We consider that the default intensity is correlated with the counterparty’s default and the interest rate following fractional Vasicek model. Moreover, we mainly discuss the CDS’s pricing that the default of the firms has an impact on each other and the default intensity has linear correlation with short-term market interest rates. In fact, we can also consider other more complex cases, such as:

Case 1: The default intensity has nonlinear correlation with short-term market interest rate;

Case 2: We can consider other economic state variables than short-term market interest rate;

Case 3: In our model, we only study two counterparts, however, there are many counterparts in the financial market and we can discuss the case of three counterparts or more in further studies.

Acknowledgements

We thank the editor and the referee for their comments. Research of W.J. Gu et al. is funded by the Innovation Program of Shanghai Municipal Education Commission (No.: 13YZ125); funding scheme for training young teachers in Shanghai Colleges (ZZshjr12010). This support is greatly appreciated.

Appendix

1) Proof of Theorem 3

Proof. Let. When, from the properties of quasi-conditional expectation ( [12] ), we have

(28)

as

(29)

so

(30)

then

(31)

and then

(32)

and when,

(33)

and when,

(34)

2) Proof of Theorem 4

Proof. Firstly, according to the pricing formula on fractional quasi-martingale in [12] and Lemma 2, we can obtain the price of bond issued by firm A at time t on is

(35)

where

(36)

()

According to Corollary 1, and then

(37)

And we find that the key step is to calculate the three quasi-conditional expectation

, ,.

As shown in the definition above, we deduce

(38)

Let,then

(39)

So

(40)

where is constant.

Let, by the definition of quasi-martingale, we show

(41)

is quasi-martingale, so

(42)

and, we can deduce

(43)

(44)

So we can get as (20). The pricing formula (21) of bond issued by firm B can be derived though the similar proving process of. Hence, we omit it. The proof is complete.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Merton, R.C. (1974) On the pricing of Corporate Debt: The Risk Structure of Interest Rates. Journal of Finance, 29, 449-470. http://dx.doi.org/10.1111/j.1540-6261.1974.tb03058.x
[2]	Jarrow R.A. and Turnbull, S.M. (1995) Pricing Derivatives on Financial Securities Subject to Credit Risk. Journal of Finance, 50, 53-85. http://dx.doi.org/10.1111/j.1540-6261.1995.tb05167.x
[3]	Duffie, J.D. and Singleton, K.J. (1999) Modeling Term Structures of Defaultable Bonds. Review of Financial Studies, 12, 687-720. http://dx.doi.org/10.1093/rfs/12.4.687
[4]	Davis, M. and Lo, V. (1999) Infectious Defaults. Quantitive Finance, 1, 382-387. http://dx.doi.org/10.1080/713665832
[5]	Jarrow, R.A. and Yu, F. (2001) Counterparty Risk and The Pricing of defaultable Securities. Journal of Finance, 56, 1765-1799. http://dx.doi.org/10.1111/0022-1082.00389
[6]	Leung, S.Y. and Kwork, Y.K. (2005) Credit Default Swap Valuation with Counterparty Risk. Kyoto Economic Review, 74, 25-45.
[7]	Collin-Dufresne, P., Goldstein, R.S. and Hugonnier, J. (2004) A General Formula for Valuaing Defaultable Securities. Econometrica, 72, 1377-1407. http://dx.doi.org/10.1111/j.1468-0262.2004.00538.x
[8]	Bai, Y.F., Hu, X.H. and Ye, Z.X. (2007) A Model for Dependent Default with Hyperbolic Attenuation Effect and Valuation of Credit Default Swap. Applied Mathematics and Mechanics (English Edition), 28, 1643-1649. http://dx.doi.org/10.1007/s10483-007-1211-9
[9]	Hao, R.L. and Ye, Z.X. (2011) The Intensity Model for Pricing Credit Securities with Jumpdiffusion and Counterparty Risk. Mathematical Problems in Engineering, 10, 1-16. http://dx.doi.org/10.1155/2011/412565
[10]	Hao, R.L. and Ye, Z.X. (2011) Pricing CDS with Jump-Diffusion Risk in the Intensity-Based Model. Advances in Intelligent and Soft Computing, 100, 221-229. http://dx.doi.org/10.1007/978-3-642-22833-9_26
[11]	Hao, R.L., Liu, Y.H. and Wang, S.B. (2014) Pricing Credit Default Swap under Fractional Vasicek Interest Rate Model. Journal of Mathematical Finance, 4, 10-20. http://dx.doi.org/10.4236/jmf.2014.41002
[12]	Hu, Y. and Øksendal, B. (2003) Fractional white Noise Calculus and Application to Finance. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 6, 1-32. http://dx.doi.org/10.1142/S0219025703001110
[13]	Huang, W.L., Tao, X.X. and Li, S.H. (2012) Pricing Formulae for European Option under the Fractional Vasicek Interest Rate Model. Acta Mathematica Sinica (in Chinese), 55, 219-230.
[14]	Lin, S.J. (1995) Stochastic Analysis of Fractional Brownian Motion, Fractional Noises and Applications. SIAM Review, 10, 422-437.
[15]	Decreusefond, L. and Ustunel, A.S. (1999) Stochastic Analysis of the Fractional Brownian Motion. Potential Analysis, 10, 177-214. http://dx.doi.org/10.1023/A:1008634027843