Re-Visiting the Decay, Missing, Filled Teeth (DMFT) Index with a Mathematical Modeling Concept ()
Received 15 November 2015; accepted 31 January 2016; published 3 February 2016
1. Introduction
Dental caries is a public oral health problem in Asia, Middle East and across the African Sub-Saharan regions [1] [2] . Although many reports worldwide agree that the presence of dental caries had declined in the population [3] , there are also, recent published studies presenting an alarming increase in the presentation of caries [4] [5] . These controversial results produced by a unique and well established methodology of measuring and rating caries among subjects, provoke and encourage epidemiologists in the field of oral health and public oral health to re-visit the DMFT index which was established more than 75 years ago.
The Decayed (D), Missing (M), Filled (F) teeth index has been used since 1938 [1] and is well established as the leading measure of caries in dental epidemiology. It has been developed by the WHO [6] to be recommended as a framework of reference to index dental caries. The index expresses the number of decayed, missing and filled teeth in a group of individuals. Despite its long use, there is a debate about the index in different aspects. Many studies criticize, the “Missing” component in the index, as it is likely to not resist the bias of recalling and this may lead to overestimation [7] [8] .
One of the obvious definitions of prevalence for a given disease is the fraction between the numbers of positively screened individuals divided by the total number screened [9] [10] . To apply this definition to the DMFT index, as the screening does clinically, the “Decayed” component of the index is clearly screened as the guidelines state [11] , as well as the “Filled” component, but the “Missing” component is not present in a cross-sec- tional design. The outcome of this component relies on the recall memory of an individual, but does not fully support the idea of screening, as pre-stated in the definition of prevalence. One of the consequences of this is the overestimation of the prevalence produced by the DMFT index. Another point of interest in index is that the index outcome relies on the individual, regardless of the number of teeth screened for the given individual. This counts individuals as a dichotomous phenomenon, for the presence or absence of caries; hence the DFMT would be greater than one, or zero, respectively. This will raise the question of what the number one hides as information concerning the severity of caries and the contribution of an individual on the cumulative probability of caries in the population when an individual makes up part of it. Using an individual as a unit of the calculation of DMFT will suggest an equally likely contribution of an individual on the ultimate prevalence of the caries of the population.
In dentistry, the DMFT index calculates different clusters per individual; the number one demonstrates the existence of caries from screening teeth, in a given environment that might be affected by other factors such as oral hygiene, public health awareness, genetic factors and the accessibility to the oral health services. These contributing factors will lead us to consider how the individual will contribute to the cumulative variance in caries as part of a given population.
The aim of the present study is to try to construct mathematical model of the existing DMFT index in order to more accurately estimate the prevalence, and consequently the average, of the DMFT index.
2. Mathematical Models
The DMF index is applied to permanent dentition and is expressed as the total number of teeth or surfaces that are Decayed (D), Missing (M) and Filled (F) for an individual. When it applied for the teeth it called DMFT, this work will focus on that. The DMFT can be arranged from 0 to 28 or to 32 depending on whether the third molars are included in the scoring. To calculate the DMFT index for an individual is given by:
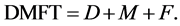(1)
The Average of the DMFT for any sample under studies is given by
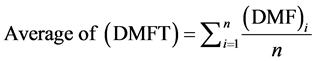(2)
where n is the size of the sample under study, and DMFT as presented on the Equation (1).
2.1. Fix Model
The Fix model is a mathematical model, that incorporate the current DMFT index as suggested by Palmar et al. (1938.), in this model, any subject under study is considered as dichotomous variable with respect to caries, i.e.
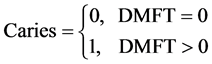(3)
So caries is a dichotomous random variable X, where X is either 0 if the DMFT is 0 or 1 if DMFT > 0, so we could consider it as a Bernoulli random variable with probability θ, 0 ≤ θ ≤ 1. Here θ remains the same for each sample and hence for every subject to have caries, then the distribution of caries is given by
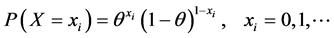(4)
For a sample of n subjects, caries for any one of these variables is a Bernoulli variable with independent and identical probability θ, as it is in fix model, hence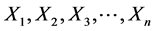 
are Bernoulli random variables independent and identically distributed with a probability of caries θ.
To find the probability of the sample, i.e.
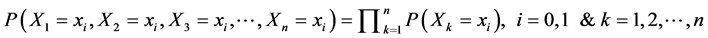(5)
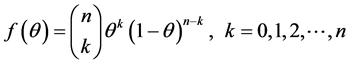(6)
Equation (6) is Binomial distribution with n and θ as parameter and k the number of subjects screened with caries, to estimate the probability θ, we find the log and we differentiate it with respect to θ, hence for the log we obtain
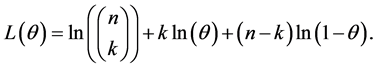
To maximize the value of θ, differentiation with respect to θ and equate to zero
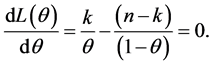
To solve the equation for θ, then we obtain
(7)
Equation (7), estimates the probability of caries (
) among n screened subjects where k of them were screened positive.
Interpretations:
The fix model assumes that caries among subjects are independently and identically distributed. It is logical to be independent, but identically distributed; such an assumption will not take into consideration many factors such as oral hygiene or the history of caries per subject.
This model does not take into account the number of teeth screened and their positions on the mouth for a subject; as it is known that not all the teeth are exposed equally to decay and not all teeth erupt at the same time.
In this model, the probability of caries will be overestimated and hence the overall estimation of the variance has no consideration of the load of participation of severity of caries per individual.
Using this model, the average of the DMFT will not consider the number of teeth screened per individual and hence this might overestimate the average of the DMFT index.
2.2. Random Model
The idea of this model is that, the mouth for every subject (j) is considered as a cluster consist of nj teeth will be screened and each tooth has an identical probability of caries θj, 0 ≤ θj ≤ 1 for each tooth in a given mouth j under investigation. In addition, the probabilities of different mouths with caries are independent
So for each tooth on the mouth j, the probability distribution of caries for a tooth is also a Bernoulli distribution variable, hence
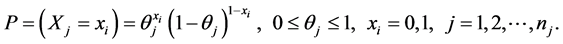(8)
Using the same derivation as above for the Equations (5) through (7), the estimation of the probability of caries for the mouth j is given by
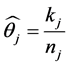
where kj number of teeth with caries and nj are number of teeth screened for the subject j.
Similarly, for every subject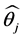 
this could be estimated. If the sample under screening with a size n, then ![]()
will be estimated for every participant. The overall estimate of the probability (![]()
) will be cal-
culated as a weighted probability depending on the probability per cluster and number of teeth screened per cluster (mouth), and it is given by
![]()
(9)
hence, ![]()
This equation means, that the probability will be given by
![]()
The number of teeth screened with caries in the sample divided by the total number of teeth actually screened (the missing teeth screened will be included in numerator and dominator) in the sample under study.
Interpretations:
The random model assumes that caries within the same subjects are independently and identically distributed but it is logical for this to be independent (eruption time and tooth position) and identically distributed (same environment).
This model takes into account the number of teeth screened and the environment in the mouth for a subject such as oral hygiene, as well as social and genetic factors and accessibility to health care facilities.
Using a tooth as a dichotomous variable; in this model; will explains the amount of variance that number of teeth for a given subject j with severity of caries will contribute on the probability of caries in a sample, as not all explain the probability with same load.
Using this model, the average of the DMFT considers the number of teeth screened per environment and hence this might accurately estimates the average of the DMFT index, as weighted mean.
![]()
3. Estimation of Variances for Two Models
3.1. Fix Model
For the fix model, based on Binomial variable parameters (n, θ), such that n is number of sample screened and θ is the probability of caries and the distribution of the probability following this probability mas function:
![]()
By using the simple formula of variance
![]()
By using characteristic function
![]()
![]()
and by differentiating the above equation with respect to θ and put t = 0, we obtain from the first and second derivative
![]()
![]()
![]()
3.2. Random Model
Using the same derivation on the fix model, for a subject j, as the phenomenon is also Binomial per mouth of subject, this will yield the same variance per subject
![]()
To calculate the overall variance, as the n subject are independent and all with Binomial distribution, then
![]()
As, subjects are independent, then
![]()
So, the variance in a random model will be the sum of variances per mouth of subjects
![]()
3.3. Theoretical Scenarios
Assume that n subjects were screened for caries in a given population, if the n subjects were screened negative for caries; (either no one with DMFT > 0 or all teeth with no caries); then the two models will yield the same probability zero and the same average of DMFT.
On the other hand if the n subjects screened with caries through all teeth screened both models will yield the same probability 1 and equal average of DMFT, and this will be given by
![]()
If among the n subjects screened, only k subjects were screened positive, then the two models will produce two different outcomes; (probability and average of DMFT).
3.3.1. Fix Model
![]()
![]()
3.3.2. Random Model
The probability will depend on the number of teeth screened on the total n subjects and the number of teeth among these k subjects screened positive with caries, hence the two parameters will be given by
![]()
kj number of teeth screened positive per subject j
![]()
It is very clear that
![]()
4. Discussion
DMFT index rates the dental caries status of an individual through scoring the actual screening units (teeth) in different environments (mouths). Although the DMFT is a simple way of characterizing the status of the dental caries of an individual, the parametrization of the indices estimated by DMFT index using an individual through multiple subunits (teeth in a mouth) is not well integrated. This does not appear in other models of diseases where the environment is unique for all individuals under screening; such as with tuberculosis, diabetes, hypertension, and HIV [12] . Certainly dental caries within a mouth is determined by a great number of variables such as biological, genetic, social and behavioral factors [13] [14] . Hence, calculation of the prevalence and average using DMFT index might not be representative to the individuals considered in the estimation of these parameters and hence the population from where these samples will be selected because of heterogeneous environments [15] . Many published studies have indicated that DMF index is not a perfect epidemiological tool, and identified number of drawbacks which have a very real detrimental effect upon estimates of caries [7] .
DMFT using a fixed model in which the probability of an individual screened positive for dental caries is the same for all individuals under screening. As dental caries a multifactorial disease affected by oral hygiene and other variables such as (biological, social and genetics factors), this is be one of the main crissa that face the DMFT index, and hence the assumption of fix probability for every individual will be unrealistic in real life. In the random model of DMFT however, the focus is to calculate the probability per individual on the function of the environment (mouth) and number of units (teeth) per individual. This will produce homogenous probabilities per individuals and hence for the overall sample screened. Such assumption will not affect the ultimate aim of DMFT to be an index that rates the oral cavity per individual, but in addition, will reflect the oral health condition per individual and hence for the entire population in a realistic manner.
The average of DMFT index calculated by the tow methods considering the same fact is the sum of overall DMFT per individual divided by the number of individuals screened for the fixed model; this simply gives all individuals the same weight of contribution on the aggregate average for the whole sample. This is not the case when we used the random model, so every individual contributing to the average by its weight on the caries depends on the number of teeth screened and number of teeth screened positive with caries. This is also logical in reflecting the real picture of the severity of caries within the population.
The usefulness of this type of analysis has an immediate impact on the epidemiology of oral health; the fixed model will overestimate the parameters (probability & average); while the random model will attempt to use logic input to estimate to some extent the realistic parameters. As long as the burden on oral health is a concern, the individual will be the ultimate target. But how many units within this individual need to be treated? From this point, the importance of a random model is needed as this reflects the real cost to tackle the burden of this oral problem. In this study we focus only in one model, the DMFT, but this approach can be extended to other indices such as, DMFS and the other oral health indices models. The practical application of this model using fresh clinical data will be the next realistic step in order to assess the strength and weakness of the model in epidemiological studies.