Received 16 December 2015; accepted 25 January 2016; published 28 January 2016

1. Introduction
Theorem 1. Let 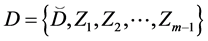 be some finite X-semilattice of unions and
be some finite X-semilattice of unions and
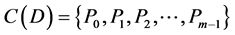
be the family of sets of pairwise nonintersecting subsets of the set X.
If φ is a mapping of the semilattice D on the family of sets  which satisfies the condition
which satisfies the condition 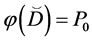 and
and 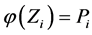 for any
for any  and
and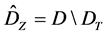 , then the following equalities are valid:
, then the following equalities are valid:
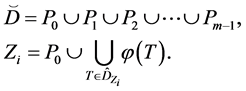 (1)
(1)
In the sequel these equalities will be called formal.
It is proved that if the elements of the semilattice D are represented in the form 1, then among the parameters Pi 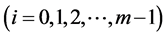 there exist such parameters that cannot be empty sets for D. Such sets Pi
there exist such parameters that cannot be empty sets for D. Such sets Pi 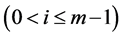 are called basis sources, whereas sets Pi
are called basis sources, whereas sets Pi 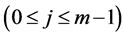 which can be empty sets too are called completeness sources.
which can be empty sets too are called completeness sources.
It is proved that under the mapping 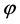 the number of covering elements of the pre-image of a basis source is always equal to one, while under the mapping
the number of covering elements of the pre-image of a basis source is always equal to one, while under the mapping ![]() the number of covering elements of the pre-image of a com- pleteness source either does not exist or is always greater than one (see [1] , Chapter 11). Some positive results in this direction can be found in [2] -[6] .
the number of covering elements of the pre-image of a com- pleteness source either does not exist or is always greater than one (see [1] , Chapter 11). Some positive results in this direction can be found in [2] -[6] .
Let ![]() be parameters in the formal equalities,
be parameters in the formal equalities, ![]() and
and
![]() (2)
(2)
![]() (3)
(3)
The representation of the binary relation ![]() of the form
of the form ![]() and
and ![]() will be called subquasinormal and maximal subquasinormal.
will be called subquasinormal and maximal subquasinormal.
If ![]() and
and ![]() are the subquasinormal and maximal subquasinormal representations of the binary relation
are the subquasinormal and maximal subquasinormal representations of the binary relation![]() , then for the binary relations
, then for the binary relations ![]() and
and ![]() the following statements are true:
the following statements are true:
a) ![]()
b) ![]()
c) the subquasinormal representation of the binary relation ![]() is quasinormal;
is quasinormal;
d) if
![]()
then ![]() is a mapping of the family of sets
is a mapping of the family of sets ![]() in the X-semilattice of unions
in the X-semilattice of unions
![]() .
.
e) if ![]() is a mapping satisfying the condition
is a mapping satisfying the condition ![]() for all
for all![]() , then
, then
![]()
2. Results
Proposition 2. Let![]() . Then
. Then
![]()
Proof. It is easy to see the inclusion ![]() holds, since
holds, since![]() . If
. If ![]()
![]() , then
, then ![]() for some
for some![]() . So,
. So, ![]() since
since ![]() and
and![]() .Then
.Then ![]() for some k
for some k ![]() i.e.
i.e. ![]() and
and![]() . For the last conditionfollows that
. For the last conditionfollows that![]() . We have
. We have ![]() and
and![]() . Therefore, the inclusion
. Therefore, the inclusion ![]() is true. Of this and by inclusion
is true. Of this and by inclusion ![]() follows that the equality
follows that the equality ![]() holds. ,
holds. ,
Corollary 1. If ![]() and
and![]() , then
, then![]() .Proof. We have
.Proof. We have ![]() and
and![]() . Of this follows that
. Of this follows that ![]() since
since![]() . ,
. ,
Let the X-semilattice ![]() of unions given by the diagram of Figure 1. Formal equalities of the given semilattice have a form:
of unions given by the diagram of Figure 1. Formal equalities of the given semilattice have a form:
![]() (4)
(4)
The parameters P1, P2, P3 are basis sources and the parameters ![]() are completeness sources, i.e.
are completeness sources, i.e.![]() .
.
Example 3. Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Then for the for-
. Then for the for-
mal equalities of the semilattice D follows that![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , and
, and
![]()
Then we have:
![]()
![]()
![]()
![]()
Theorem 4. Let the X-semilattice ![]() of unions given by the diagram of Figure 1,
of unions given by the diagram of Figure 1,
![]() and
and![]() . Then the set B is generating set of the semigroup
. Then the set B is generating set of the semigroup![]() .
.
Proof. It is easy to see that ![]() since
since ![]() and
and![]() . Now, let
. Now, let ![]() be any binary rela- tion of the semigroup
be any binary rela- tion of the semigroup![]() ;
;![]() ,
, ![]() and
and![]() . Then the equality
. Then the equality ![]() (
(![]() is subquasinormal representation of a binary relation
is subquasinormal representation of a binary relation![]() ) is true. By assumption
) is true. By assumption![]() , i.e. the quasinormal representation of a binary relation
, i.e. the quasinormal representation of a binary relation ![]() have a form
have a form
![]()
Of this follows that
![]() (5)
(5)
For the binary relation ![]() we consider the following case.
we consider the following case.
a) Let![]() . Then
. Then![]() , where
, where![]() . By element T we consider the following cases:
. By element T we consider the following cases:
1.![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (6)
(6)
where![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (6) and (5) we have:
. From the formal equality and equalities (6) and (5) we have:
![]()
since![]() .
.
2.![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() in the set D. Then
in the set D. Then
![]() (7)
(7)
where![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (7) and (5) we have:
. From the formal equality and equalities (7) and (5) we have:
![]()
b)![]() . Then
. Then
![]()
since ![]() is X-semilattice of unions. For the semilattice of unions
is X-semilattice of unions. For the semilattice of unions ![]() consider the following cases.
consider the following cases.
1. Let![]() , where,
, where,![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (8)
(8)
where![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that
![]() since
since![]() . From the formal equality and equalities (8) and (5) we have:
. From the formal equality and equalities (8) and (5) we have:
![]()
2. Let![]() , where,
, where,![]() . Then binary relation
. Then binary relation ![]() has representation of the
has representation of the
form![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (9)
(9)
where![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that
![]() since
since![]() . From the formal equality and equalities (9) and (5) we have:
. From the formal equality and equalities (9) and (5) we have:
![]()
c)![]() . Then
. Then
![]()
since ![]() is X-semilattice of unions. For the semilattice of unions
is X-semilattice of unions. For the semilattice of unions ![]() consider the following cases.
consider the following cases.
1. Let![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form
![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (10)
(10)
where![]() ,
, ![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that
![]() since
since![]() . From the formal equality and equalities (10) and (5) we have:
. From the formal equality and equalities (10) and (5) we have:
![]()
2. Let![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form
![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (11)
(11)
where![]() ,
, ![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (11) and (5) we have:
. From the formal equality and equalities (11) and (5) we have:
![]()
3. Let![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form
![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (12)
(12)
where![]() ,
, ![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (12) and (5) we have:
. From the formal equality and equalities (12) and (5) we have:
![]()
4. Let![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form
![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (13)
(13)
where![]() ,
, ![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (13) and (5) we have:
. From the formal equality and equalities (13) and (5) we have:
![]()
5. Let![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form
![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (14)
(14)
where![]() ,
, ![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (14) and (5) we have:
. From the formal equality and equalities (14) and (5) we have:
![]()
6. Let![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form
![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (15)
(15)
where![]() ,
, ![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (15) and (5) we have:
. From the formal equality and equalities (15) and (5) we have:
![]()
7. Let![]() . Then binary relation
. Then binary relation ![]() has representation of the form
has representation of the form
![]() . In this case suppose that
. In this case suppose that
![]()
and ![]() are mapping of the set
are mapping of the set ![]() on the set
on the set![]() . Then
. Then
![]() (16)
(16)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , then it is easy to see, that
, then it is easy to see, that ![]() since
since![]() . From the formal equality and equalities (16) and (5) we have:
. From the formal equality and equalities (16) and (5) we have:
![]()
,