Received 20 November 2015; accepted 22 January 2016; published 25 January 2016

1. Introduction
There are so many studies in the literature that are concern about special number sequences such as Fibonacci, Lucas, Pell, Jacobsthal, and Padovan in [1] [2] . They are widely used in many research areas as Engineering, Architecture, Nature and Art in [3] -[6] . For example, microcontrollers (and other computers) use conditional instructions to change the flow of execution of a program. In addition to branch instructions, some micro- controllers use skip instructions which conditionally bypass the next instruction. This winds up being useful for one case out of the four possibilities on 2 bits, 3 cases on 3 bits, 5 cases on 4 bits, 21 on 6 bits, 43 on 7 fits, 85 on 8 fits, ..., which are exactly the Jacosthal numbers [7] . Jacobsthal and Jacobsthal Lucas numbers are given by the recurrence relations 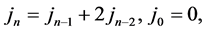
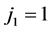 and
and 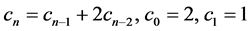 for
for 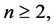 res- pectively in [7] - [9] . Generalization of number sequences is studied in many articles. For example the gener- alization of Jacobsthal sequences is defined in [10] . We can see any properties of these numbers in [7] - [9] [11] [12] . Some properties of these sequences were deduced directly from elementary matrix algebra in [13] [14] . By using matrix algebra H. Civciv and R. Turkmen defined
res- pectively in [7] - [9] . Generalization of number sequences is studied in many articles. For example the gener- alization of Jacobsthal sequences is defined in [10] . We can see any properties of these numbers in [7] - [9] [11] [12] . Some properties of these sequences were deduced directly from elementary matrix algebra in [13] [14] . By using matrix algebra H. Civciv and R. Turkmen defined 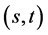 Fibonacci and
Fibonacci and 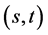 Lucas matrix sequences in [15] [16] . Similarly K. Uslu and Ş. Uygun defined
Lucas matrix sequences in [15] [16] . Similarly K. Uslu and Ş. Uygun defined 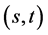 Jacosthal and
Jacosthal and 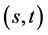 Jacosthal Lucas matrix se- quences and by using them found some properties of Jacobsthal numbers in [17] .
Jacosthal Lucas matrix se- quences and by using them found some properties of Jacobsthal numbers in [17] .
Definition 1. The (s,t)-Jacobsthal sequence 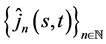 and (s,t)-Jacobsthal Lucas sequence
and (s,t)-Jacobsthal Lucas sequence 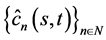 are defined by the recurrence relations
are defined by the recurrence relations
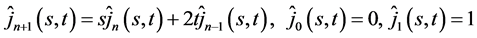 (1)
(1)
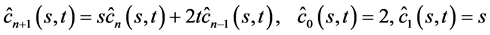 (2)
(2)
respectively, where 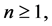
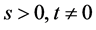 and
and 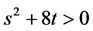 [10] .
[10] .
Some basic properties of these sequences are given in the following:
![]()
![]()
![]()
![]()
In the following definition, (s,t)-Jacosthal ![]() and (s,t)-Jacosthal Lucas
and (s,t)-Jacosthal Lucas ![]() matrix se- quences are defined by carrying to matrix theory (s,t)-Jacosthal and (s,t)-Jacosthal Lucas sequences.
matrix se- quences are defined by carrying to matrix theory (s,t)-Jacosthal and (s,t)-Jacosthal Lucas sequences.
Definition 2. The (s,t)-Jacobsthal matrix sequence ![]() and (s,t)-Jacobsthal Lucas matrix sequence
and (s,t)-Jacobsthal Lucas matrix sequence ![]() are defined by the recurrence relations
are defined by the recurrence relations
![]() (3)
(3)
![]() (4)
(4)
respectively, where ![]()
![]() and
and ![]()
Throughout this paper, for convenience we will use the symbol ![]() instead of
instead of ![]() and the symbol
and the symbol ![]() instead of
instead of![]() . Similarly we will use the symbol
. Similarly we will use the symbol ![]() instead of
instead of ![]() and
and ![]() instead of
instead of ![]()
Proposition 3. Let us consider ![]() and
and ![]() The following properties are hold:
The following properties are hold:
1) ![]() and
and ![]()
2) For ![]()
![]()
3) For ![]()
![]()
4) For ![]()
![]()
For their proofs you can look at the Ref. [17] .
2. The Generating Functions of Jacobsthal and Jacobsthal-Lucas Matrix Sequences
Theorem 4. For ![]()
![]() we have the generating function of Jacobsthal matrix sequence in the following:
we have the generating function of Jacobsthal matrix sequence in the following:
![]() (5)
(5)
Proof. By using the expansion of geometric series and proposition 3, we can write
![]()
■
Corollary 5. Let ![]() Then for (s,t)-Jacobsthal sequence we have
Then for (s,t)-Jacobsthal sequence we have
![]()
and
![]()
Corollary 6. Let ![]() Then we have
Then we have
![]()
Corollary 7. Let ![]() Then we have we have the generating function of Jacobsthal-Lucas matrix sequence in the following:
Then we have we have the generating function of Jacobsthal-Lucas matrix sequence in the following:
![]() (6)
(6)
Proof. It can be seen easily by using theorem 4 and the property of ![]() ■
■
Corollary 8. Let ![]() Then for (s,t)-Jacobsthal Lucas matrix sequence we have
Then for (s,t)-Jacobsthal Lucas matrix sequence we have
![]()
Corollary 9. Let ![]() Then for (s,t)-Jacobsthal Lucas sequence we have
Then for (s,t)-Jacobsthal Lucas sequence we have
![]()
and
![]()
Theorem 10. For ![]() let be r is odd positive integer and
let be r is odd positive integer and ![]()
![]()
Then we have
![]()
and for r is even positive integer
![]()
Proof. By using proposition 3 (iv), the nth element of (s,t)-Jacobsthal matrix sequence can be written in the following:
![]()
From this equality we have
![]()
![]()
If r is an odd positive integer, then we have
![]()
If r is an even positive integer, then we have
![]()
■
3. Partial Sums of Jacobsthal and Jacobsthal-Lucas Matrix Sequences
Theorem 11. The partial sum of (s,t)-Jacobsthal matrix sequence for ![]() is given in the following
is given in the following
![]()
Proof. Let![]() . By multiplying
. By multiplying ![]() two sides of the equality, we get
two sides of the equality, we get
![]()
By adding ![]() two sides of the equality, we get
two sides of the equality, we get
![]()
![]()
![]()
The inverse of ![]() is available for
is available for![]() . Then we get
. Then we get
![]()
By using following equalities ![]()
![]() and
and
![]() we get
we get
![]()
■
Corollary 12. The partial sums of (s,t)-Jacobsthal sequence for ![]() are given in the following:
are given in the following:
![]()
and
![]()
Proof. It is proved by the equality of matrix sequences and from Theorem 11. ■
Theorem 13. The partial sum of (s,t)-Jacobsthal Lucas matrix sequence for ![]() is given in the follow-
is given in the follow-
ing ![]()
![]()
![]()
![]()
![]()
Proof. By using ![]() and Theorem 11 we get
and Theorem 11 we get
![]()
If the product of matrices is made the desired result is found. ■
Corollary 14. The partial sums of (s,t)-Jacobsthal Lucas sequence for ![]() are given in the following:
are given in the following:
![]()
and
![]()
Proof. It is proved by the equality of matrix sequences and from Theorem 11. ■
Theorem 15. Let ![]() and
and ![]() Then for
Then for ![]() we get
we get
![]()
![]()
![]()
![]()
Proof. By multiplying ![]() two sides of the equality
two sides of the equality![]() , we get
, we get
![]()
By adding ![]() two sides of the equality, we get
two sides of the equality, we get
![]()
![]()
![]()
![]()
![]()
![]()
■
Corollary 16. The odd and even elements sums of (s,t)-Jacobsthal sequence for ![]() and
and ![]() are given in the following:
are given in the following:
![]()
![]()
In the following theorem we will show the partial sum of Jacobsthal Lucas matrix sequence of the elements of power of n.
Theorem 17. For (s,t)-Jacobsthal matrix sequence the equality is hold.
![]()
Proof. By using the equality of ![]() we can write
we can write ![]() By using it
By using it
![]()
■
Acknowledgements
Thank you very much to the editor and the referee for their valuable comments.