Hydrodynamic Anisotropy Effects on Radiation-Mixed Convection Interaction in a Vertical Porous Channel ()
Received 10 December 2015; accepted 11 January 2016; published 14 January 2016

1. Introduction
Convection heat transfer in porous media is a fundamental importance in such technologies as geothermal exploitation, oil recovery, radioactive waste management, insulation of building and cold storage, drying processes, transpiration cooling, powder metallurgy, agricultural engineering, solidification and binary alloys, etc. It is also important to geophysics and environmental sciences. Much of this activity, both numerical and experimental, has been summarized by Nield and Bejan (1999) [1] . Moreover, a relevant recent work on the topic is done by Chen et al. (2000) [2] .
Thermal radiation always exists and can strongly interact with convection in many situations of engineering interest. The convection heat transfer in a porous channel (or in an enclosed space) in the presence of thermal radiation continues to receive considerable attention because of its importance in many practical applications such as furnaces, combustion chambers, cooling towers, rocket engines and solar collectors. During the last decade, many experimental and numerical investigations on the phenomenon of the interaction of natural or mixed convection with thermal radiation in vertical porous channels or enclosures have been presented. Mahmud and Fraser (2003) [3] have examined analytically the effects of radiation heat transfer on magnetohydrodynamic mixed convection through a vertical channel packed with fluid saturated porous substances. Basing their analysis on the first and second laws of thermodynamics, these authors have given special attention to entropy generation characteristics and their dependency on the various governing parameters of the problem. Jbara et al. (2011) [4] have conducted a numerical study to investigate the effects of the radiation heat transfer on the transient natural convection in a vertical channel opened at both ends and filled with a fluid saturated porous medium. Taking into account the Rosseland approximation in the energy equation, they have showed that approximation is only valid for large Planck number values for temperature ratios closed to unity and/or for single scattering albedo near or equals to one. An unsteady natural convection magnetohydrodynamic flow of a rotating viscous electrically fluid in a vertical channel with radiation effects has been investigated by Chauban and Rastogi (2010) [5] who obtained analytical expressions for velocity and temperature fields and discussed the effects of radiation on the phenomenon. A transient study of coupled natural convection and radiation in a porous vertical channel using the finite- volume method has been conducted by Slimi et al. (2004) [6] . The results indicated that the controlling parameters of the problem have significant effects on the flow and the thermal fields and on the transient process of heating and cooling of the medium. They have demonstrated that the volumetric flow rate and the convected heat flux at the channel’s exit increase when the Planck number is decreased and/or the optical thickness and the wall emissivity are increased.
Most of the existing theories and experimental investigations on the topic, are concerned isotropic porous media. However, in several applications the porous materials are anisotropic. Such porous media are in fact encountered in numerous systems in industry and nature. As examples, we can cite fibrous materials, biological materials, geological formations, and oil extraction. The inclusion of more physical realism in the matrix properties of the medium is important for the accurate modeling of the anisotropic media. Anisotropy is generally a consequence of a preferential orientation and asymmetric geometry of the grain or fibbers which constitute the porous medium. Despite its vast range of applications, convection in such anisotropic porous media has received relatively little attention.
Thermal convection in a porous medium with anisotropic permeability was first considered by Castinel and Combarnous (1974) [7] who conducted an experimental and theoretical investigation in a horizontal layer heated from below. Their results were extended by Epherre (1975) [8] and Kvernvold and Tyvand (1979) [9] who considered a more general type of anisotropy. Convection attributable to side-heating in a vertical layer has been considered by several authors. For example, the case of square cavity with homogeneous media that is both thermally and hydrodynamically anisotropic has been investigated analytically by Kimura et al. (1993) [10] and numerically by Ni and Beckermann (1991) [11] . The effect of both anisotropy of permeability and thermal conductivity on the overall Nusselt number was found to be equally significant. A few studies have also been concerned with the case when the principal axes of anisotropy of the porous structure are inclined with respect to the gravity force. For this situation, the onset of motion in a porous layer heated from below was predicted by Tyvand and Storesletten (1991) [12] and Zhang et al. (1993) [13] . It was demonstrated that the influence of the anisotropy orientation considerably modifies the stability limit. Convection heat transfer in a vertical cavity heated from the side with various thermal boundary conditions has been investigated by Zhang (1993) [14] , Degan et al. (1995) [15] and Degan and Vasseur (1997, 2002) [16] [17] . It was demonstrated that the heat transfer was maximum when the principal axis with higher permeability is parallel to the vertical direction and minimum when it is perpendicular.
The contemporary trend in the field of heat transfer and thermal design is to apply a second law of thermodynamics analysis, and its design-related concept of entropy generation minimization (see Bejan (1996) [18] ). Entropy generation is associated with thermodynamic irreversibility which is present in all heat transfer processes. Because of the abundance of publications on entropy, no attempt is made here to review the literature.
The present work deals with an analytical study of coupled fluid flow and heat transfer by mixed convection and radiation in a vertical channel opened at both ends and filled with a fluid-saturated porous medium. The bounding walls of the channel are isothermal and gray. The effects of hydrodynamic anisotropy of the porous medium will be investigated, since the physical problem is of significant importance to many engineering-related applications.
2. Mathematical Formulation
The problem, under different considerations, concerns an optically thin and electrically conducting fluid flowing through a vertical channel opened at both ends and filled with a porous medium as shown by the physical model considered in Figure 1. The bounding walls of the channel are isothermal and kept at the same or different temperatures. Moreover, these bounding walls are submitted to the influence of radiative intensities 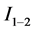 and
and 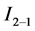 exerting reciprocally actions on the right and the left walls, respectively. The depth of the channel along the
exerting reciprocally actions on the right and the left walls, respectively. The depth of the channel along the 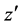 - axis is assumed sufficiently long compared to other directions,
- axis is assumed sufficiently long compared to other directions, 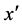 being the direction of the flow and
being the direction of the flow and 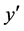 - direction perpendicular to that latter. A fully developed, laminar and induced flow is maintained through this porous channel upward, so that the natural convection aids the forced flow. As considered in nature in fact, the porous medium is anisotropic in flow permeability, the permeabilities along the two principal axes of the porous matrix are denoted by
- direction perpendicular to that latter. A fully developed, laminar and induced flow is maintained through this porous channel upward, so that the natural convection aids the forced flow. As considered in nature in fact, the porous medium is anisotropic in flow permeability, the permeabilities along the two principal axes of the porous matrix are denoted by 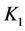 and
and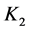 . The anisotropy in flow permeability of the porous medium is then characterized by the permeability ratio
. The anisotropy in flow permeability of the porous medium is then characterized by the permeability ratio 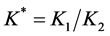 and the orientation
and the orientation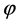 , defined as the angle between the horizontal direction and the principal axis with permeability
, defined as the angle between the horizontal direction and the principal axis with permeability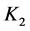 . The principal directions of the thermal conductivity are assumed to coincide to those of the coordinate axes. The saturating fluid is viscous, incompressible and assumed to be in local thermodynamic equilibrium with the solid matrix everywhere and its thermophysical properties are assumed constant, except for the density in the buoyancy term in the momentum equation.
. The principal directions of the thermal conductivity are assumed to coincide to those of the coordinate axes. The saturating fluid is viscous, incompressible and assumed to be in local thermodynamic equilibrium with the solid matrix everywhere and its thermophysical properties are assumed constant, except for the density in the buoyancy term in the momentum equation.
Under the above approximations, the equations governing the conservation of mass, momentum (generalized Brinkman-extended Darcy’s law) and energy can be written as follows (see [3] [17] ):
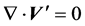 (1)
(1)
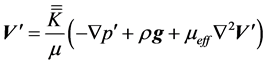 (2)
(2)
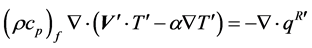 (3)
(3)
where 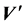 is the superficial flow velocity,
is the superficial flow velocity, 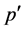 is the pressure,
is the pressure, ![]() the dynamic viscosity,
the dynamic viscosity, ![]() apparent dynamic viscosity for Brinkman’s model,
apparent dynamic viscosity for Brinkman’s model, ![]() the heat capacity of the fluid,
the heat capacity of the fluid, ![]() the density,
the density, ![]() the thermal diffusivity,
the thermal diffusivity, ![]() the temperature and
the temperature and ![]() represents the radiative heat flux. The symmetrical second-order permeability tensor
represents the radiative heat flux. The symmetrical second-order permeability tensor ![]() is defined as:
is defined as:
![]()
Figure 1. Physical model of the channel.
![]() (4)
(4)
The energy Equation (3) takes into account the radiative heat flux term![]() . It is a non-linear term which will be evaluate to have approximate analytical solution for the present problem. Due to the fact that the radiative heat flux is normal to the bounding walls,
. It is a non-linear term which will be evaluate to have approximate analytical solution for the present problem. Due to the fact that the radiative heat flux is normal to the bounding walls, ![]() and only the term
and only the term ![]() will be considered in the energy equation, and for which an approximate mathematical model will be estimated. According to Arpaci et al. [19] , one can write as follows:
will be considered in the energy equation, and for which an approximate mathematical model will be estimated. According to Arpaci et al. [19] , one can write as follows:
![]() (5)
(5)
where![]() ,
, ![]() and
and ![]() are the monochromatic absorption coefficient, solid angle, and blackbody emissive power, respectively. The second term at the right hand side of Equation (5) represents the effect of boundaries. Assuming hemispherical isotropy, and replacing actual intensity with two-stream intensities (outward and inward) as shown in Figure 1, the second term of the right hand side of Equation (5) can be written as
are the monochromatic absorption coefficient, solid angle, and blackbody emissive power, respectively. The second term at the right hand side of Equation (5) represents the effect of boundaries. Assuming hemispherical isotropy, and replacing actual intensity with two-stream intensities (outward and inward) as shown in Figure 1, the second term of the right hand side of Equation (5) can be written as ![]() and
and ![]() are the monochromatic absorption coefficient, solid angle, and blackbody emissive power, respectively. The second term at the right hand side of Equation (5) represents the effect of boundaries. Assuming hemispherical isotropy, and replacing actual intensity with two-stream intensities (outward and inward) as shown in Figure 1, the second term of the right hand side of Equation (5) can be written as
are the monochromatic absorption coefficient, solid angle, and blackbody emissive power, respectively. The second term at the right hand side of Equation (5) represents the effect of boundaries. Assuming hemispherical isotropy, and replacing actual intensity with two-stream intensities (outward and inward) as shown in Figure 1, the second term of the right hand side of Equation (5) can be written as
![]() (6)
(6)
Considering that the absorption is negligible for a thin gas, ![]() and
and ![]() remain uniform across the thickness of the gas between the plates (see Figure 1). Consequently,
remain uniform across the thickness of the gas between the plates (see Figure 1). Consequently, ![]() and
and ![]() become identical. Approximating each stream as a relation between emission
become identical. Approximating each stream as a relation between emission ![]() and reflexion
and reflexion![]() ,
, ![]() and
and ![]() can be written as
can be written as
![]() (7)
(7)
where ![]() and
and ![]() are the intensities of radiation,
are the intensities of radiation, ![]() and
and ![]() the emissivities, and
the emissivities, and ![]() and
and ![]() the reflectivities on the left and the right bounding walls, respectively.
the reflectivities on the left and the right bounding walls, respectively.
Solving the system of equations, Equations (7a) and (7b), the solutions for ![]() and
and ![]() yield
yield
![]() (8)
(8)
Substituting results obtained for these intensities into Equation (6) and noting that ![]() (the transmissivity being negligible in this study) and
(the transmissivity being negligible in this study) and![]() , one can have the following approximation
, one can have the following approximation
![]() (9)
(9)
where ![]() and
and ![]() are the monochromatic absorption coefficients on the left and the right walls, respectively.
are the monochromatic absorption coefficients on the left and the right walls, respectively.
Taking into account that the emissivities of the left and the right walls are identical, (i.e.,![]() ), the substitution of Equation (9) into Equation (5) yields
), the substitution of Equation (9) into Equation (5) yields
![]() (10)
(10)
In the above equation, ![]() can be replaced by the mean emissive power
can be replaced by the mean emissive power![]() , such that the two terms,
, such that the two terms, ![]() and
and ![]() can be further expressed as
can be further expressed as ![]() and
and![]() , where
, where ![]() is the Stefan-Boltzmann constant. These terms in
is the Stefan-Boltzmann constant. These terms in ![]() appearing in the energy equation have to be linearized in order to obtain analytical solution. Expressing T as a Taylor series about
appearing in the energy equation have to be linearized in order to obtain analytical solution. Expressing T as a Taylor series about ![]() with the assumption of small
with the assumption of small ![]() yields
yields
![]() (11)
(11)
Truncating the above series after the second term and using the definitions of ![]() and
and![]() , Equations (10) and (11) yield
, Equations (10) and (11) yield
![]() (12)
(12)
Introducing the Boussinesq approximation
![]() (13)
(13)
and assuming that when the flow is fully developed in the channel, the axial (x’-direction) velocity depends only of the transverse coordinate y’ (i.e.,![]() ), and then from the continuity equation, the transverse velocity component must be zero (i.e.,
), and then from the continuity equation, the transverse velocity component must be zero (i.e.,![]() ). Moreover, accounting for uniform wall temperature, one gets
). Moreover, accounting for uniform wall temperature, one gets![]() , and the governing equations (for steady convective flow) may be written in reduced form as
, and the governing equations (for steady convective flow) may be written in reduced form as
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
where
![]() (18)
(18)
The hydrodynamic and thermal boundary conditions for the vertical channel are
![]() (19)
(19)
![]() (20)
(20)
Taking ![]() (and d),
(and d), ![]() ,
, ![]() and
and ![]() as respective dimensional scales for length
as respective dimensional scales for length ![]() (and
(and![]() ), velocities
), velocities ![]() and
and![]() , pressure and temperature, the governing Equations (14) and (17) can be written in nondimensional form as
, pressure and temperature, the governing Equations (14) and (17) can be written in nondimensional form as
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
where
![]() (25)
(25)
In the above equation, ![]() is the Darcy-modified Rayleigh number based in permeability
is the Darcy-modified Rayleigh number based in permeability![]() ,
, ![]() the Reynolds number,
the Reynolds number, ![]() the Darcy number,
the Darcy number, ![]() the Peclet number,
the Peclet number, ![]() the Prandtl number,
the Prandtl number, ![]() the Planck number and
the Planck number and ![]() the dimensionless optical thickness. The dimensionless temperature T is defined as
the dimensionless optical thickness. The dimensionless temperature T is defined as ![]() where
where ![]() is the reference temperature. For
is the reference temperature. For
the reference temperature difference, ![]() , assuming that
, assuming that![]() , one can chose
, one can chose![]() .
.
The boundary conditions, Equations (19) and (20) become
![]() (26)
(26)
![]() (27)
(27)
where![]() .
.
From the dimensionless Equations (21) and (24) and the boundary conditions Equations (26) and (27), it is seen that the present problem is governed by eight dimensionless parameters, namely![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . However, in the present study, the value of
. However, in the present study, the value of ![]() in Brinkman’s extension is taken, as a first approximation, equal to
in Brinkman’s extension is taken, as a first approximation, equal to ![]() (i.e.,
(i.e.,![]() ).
).
3. Analysis
3.1. Fully Developed Flow Solution
Using the boundary conditions for the temperature, Equation (24) can be integrated to give the following fully developed temperature profile
![]() (28)
(28)
By substituting Equation (28) into Equation (22), and using the boundary conditions, Equations (26) and (27), the velocity profile is obtained as follows
![]() (29)
(29)
where
![]() (30)
(30)
In the above expression of the distribution of the velocity, the parameter ![]() still remains to be evaluated. Substituting of Equation (29) into the continuity Equation (21) then gives directly the pressure variation as
still remains to be evaluated. Substituting of Equation (29) into the continuity Equation (21) then gives directly the pressure variation as
![]() (31)
(31)
It is noticed that when![]() , one can find that
, one can find that
![]() (32)
(32)
This result is in agreement with that which has been found by Degan and Vasseur [17] .
The wall friction is defined by the following expression
![]() (33)
(33)
where the plus and minus signs correspond to the left and the right walls. Hence, on the left wall the friction is expressed as follows
![]() (34)
(34)
while, on the right wall, for the friction one can have
![]() (35)
(35)
such that the average friction defined by ![]() is expressed as follows
is expressed as follows
![]() (36)
(36)
where
![]() (37)
(37)
Concerning theory of fully developed confined convection including flow reversal in vertical channels, when buoyancy effects are increased (i.e., when the heat flux is increased), the fluid will accelerate near the walls. Then, mass conservation requires that the fluid decelerates in the center of the channel. Consequently, if buoyancy effects are strong enough, a minimum will form in the velocity distribution at the channel centerline. For even stronger buoyancy effects, a flow reversal will form at the channel centerline. In the case of aiding mixed convection through the porous channel, when a reverse flow occurs, the relatively lower velocity negative flow passes along side the cold wall hence carries a lower level of thermal energy. Since a net dimensionless mass flow is fixed, an equal quantity of fluid is added to the fluid flowing in the positive (upward) direction in this fluid flows adjacent to the hot wall thereby carrying a larger amount of energy.
Following Aung and Worku [20] and many authors, it is possible to deduce an expression or a criterion by which to predict whether flow reversal occurs. It is seen that, when![]() , the occurrence of flow reversal is given by the condition
, the occurrence of flow reversal is given by the condition
![]() (38)
(38)
Applying Equation (29), the above condition translates into
![]() (39)
(39)
where
![]() (40)
(40)
Accordingly, one can deduce the flow reversal function ![]() as
as
![]() (41)
(41)
Two cases are of interest, one with ![]() and the other with
and the other with![]() .
.
・ Case with ![]() (i.e.,
(i.e.,![]() ): This case corresponds to a weaker anisotropic porous medium situation for which the resistance resulting from the boundary effects is predominant with respect to that due to the solid matrix, as
): This case corresponds to a weaker anisotropic porous medium situation for which the resistance resulting from the boundary effects is predominant with respect to that due to the solid matrix, as ![]() when
when![]() . This situation approaches to the fluid medium case in which the anisotropic effects of the porous medium are irrelevant. As a result, the pressure gradient, from Equation (31), is given by
. This situation approaches to the fluid medium case in which the anisotropic effects of the porous medium are irrelevant. As a result, the pressure gradient, from Equation (31), is given by
![]() (42)
(42)
Consequently, as ![]() goes to zero, the limit of the pressure gradient is written as
goes to zero, the limit of the pressure gradient is written as
![]() (43)
(43)
Then, the velocity profile, Equation (29) and its limit, as ![]() goes to zero, become as follows
goes to zero, become as follows
![]() (44)
(44)
and
![]() (45)
(45)
The average friction and its limit, as ![]() goes to zero, are
goes to zero, are
![]() (46)
(46)
and
![]() (47)
(47)
Also, the flow reversal function, Equation (41) and its limit can be written as
![]() (48)
(48)
and
![]() (49)
(49)
Consequently, as ![]() goes to zero, applying Equation (49), the function of the flow reversal function’s limit and its limit
goes to zero, applying Equation (49), the function of the flow reversal function’s limit and its limit
![]() (50)
(50)
![]() (51)
(51)
Similar results has been obtained by Degan and Vasseur [17] . The same remark is also made when comparing the result above with that one obtained by Aung and Worku [20] for the situation corresponding to a pure fluid medium in absence of radiation condition imposed on the walls.
・ Case with ![]() (i.e.,
(i.e.,![]() ): This case corresponds to a low porosity medium (the Darcy medium situation) in which the anisotropic effects are predominant, as
): This case corresponds to a low porosity medium (the Darcy medium situation) in which the anisotropic effects are predominant, as ![]() when
when![]() . In this situation, one can obtain the following results for the velocity profile and its limit
. In this situation, one can obtain the following results for the velocity profile and its limit
![]() (52)
(52)
and
![]() (53)
(53)
Also, in this limiting situation, the pressure gradient, the average friction and the flow reversal function are expressed as follows
![]() (54)
(54)
![]() (55)
(55)
and
![]() (56)
(56)
3.2. Limiting Case of Forced Convection Solution
The limiting case of forced convection solution is obtained by setting ![]() in Equation (29). Then the velocity distribution is given by
in Equation (29). Then the velocity distribution is given by
![]() (57)
(57)
Here, the pressure variation is determined by the following expression
![]() (58)
(58)
The results presented above will be specified for two cases of interest (![]() and
and![]() ).
).
・ ![]() : For this case, the velocity profile is expressed as
: For this case, the velocity profile is expressed as
![]() (59)
(59)
The pressure gradient is written
![]() (60)
(60)
・ ![]() : In this situation, one can obtain the following results for the velocity profile
: In this situation, one can obtain the following results for the velocity profile
![]() (61)
(61)
and for the pressure gradient
![]() (62)
(62)
3.3. Limiting Case of Natural Convection Solution
This important limiting case will be studied by setting![]() . For natural convection, the entrance velocity cannot be specified. In this case, new dimensionless variables should be used as
. For natural convection, the entrance velocity cannot be specified. In this case, new dimensionless variables should be used as
![]() (63)
(63)
and, as ![]() in this study, Equation (22) can be rewritten as follow
in this study, Equation (22) can be rewritten as follow
![]() (64)
(64)
The solution for the velocity distribution may be written in terms of variables utilized herein, giving
![]() (65)
(65)
In the above velocity profile, the corresponding expressions to B and C are those indicated in Equation (30).
Taking![]() , one obtains similar profile to that one obtained by Degan and Vasseur [18] .
, one obtains similar profile to that one obtained by Degan and Vasseur [18] .
The volume flow rate b per unit channel width is defined as ![]() which becomes in dimensionless form as
which becomes in dimensionless form as
![]() (66)
(66)
that must be calculated by the expression
![]() (67)
(67)
When![]() , Equation (67) gives similar expression to that one obtained by Degan and Vasseur [17] corresponding to the case studied here when the radiation effect on the side walls is not taken into account.
, Equation (67) gives similar expression to that one obtained by Degan and Vasseur [17] corresponding to the case studied here when the radiation effect on the side walls is not taken into account.
The total heat absorbed by the fluid in traversing the channel is
![]() (68)
(68)
Writting ![]() in its dimensionless form and using Equations (28) and (65), the total heat absorbed is obtained as
in its dimensionless form and using Equations (28) and (65), the total heat absorbed is obtained as
![]() (69)
(69)
where B and C are the corresponding expressions indicated in Equation (30).
An average Nusselt number may be defined as
![]() (70)
(70)
where ![]() is the Darcy-modified Rayleigh number and Q the total heat absorbed, calculated in Equation (69).
is the Darcy-modified Rayleigh number and Q the total heat absorbed, calculated in Equation (69).
The flow reversal condition for the limiting case of natural convection is
![]() (71)
(71)
such that the flow reversal criterion becomes
![]() (72)
(72)
Taking![]() , one obtains from Equation (72), similar flow reversal occurrence criterion to that one obtained by Degan and Vasseur [17] .
, one obtains from Equation (72), similar flow reversal occurrence criterion to that one obtained by Degan and Vasseur [17] .
We notice here two cases of interest, the first one with ![]() and the second with
and the second with![]() .
.
・ ![]() : The velocity and the flow rate and their limiting values as
: The velocity and the flow rate and their limiting values as ![]() goes to zero are calculated as
goes to zero are calculated as
![]() (73)
(73)
![]() (74)
(74)
and
![]() (75)
(75)
![]() (76)
(76)
・ ![]() :It is found in this case that, the velocity and the flow volume rate and the average Nusselt number are expressed as follows
:It is found in this case that, the velocity and the flow volume rate and the average Nusselt number are expressed as follows
![]() (77)
(77)
![]() (78)
(78)
![]() (79)
(79)
It is noticed that when![]() , one can find that
, one can find that
![]() (80)
(80)
Similar result has been found by Degan and Vasseur [17] for analogous situation when the thermal radiation effect is not taking into account.
4. Results and Discussion
The effects of varying![]() , the radiation parameter,
, the radiation parameter, ![]() and
and![]() , the anisotropic parameters on the velocity profile for the case of mixed convection using Equation (29) are presented in Figures 2-4 for
, the anisotropic parameters on the velocity profile for the case of mixed convection using Equation (29) are presented in Figures 2-4 for![]() ,
, ![]() and
and![]() .
.
In Figure 2, the radiation parameter ![]() affects the flow by promoting the convective circulation within the channel near the hot wall. The inverse behavior is obtained when
affects the flow by promoting the convective circulation within the channel near the hot wall. The inverse behavior is obtained when ![]() for which a reverse flow is observed as the fluid near the cold wall sinks and the velocity decreases more and more. Such a conclusion has also been made by Degan and Vasseur [17] when studying mixed-convection through a vertical anisotropic porous channel with oblique principal axes without radiation effect. Aung and Worku [20] explained that, the reverse motion which occurs in the flow field is due to the fact that the ratio of wall temperature differences
for which a reverse flow is observed as the fluid near the cold wall sinks and the velocity decreases more and more. Such a conclusion has also been made by Degan and Vasseur [17] when studying mixed-convection through a vertical anisotropic porous channel with oblique principal axes without radiation effect. Aung and Worku [20] explained that, the reverse motion which occurs in the flow field is due to the fact that the ratio of wall temperature differences ![]() is less than unity.
is less than unity.
From Figure 3 and Figure 4, when![]() ,
, ![]() ,
, ![]() and
and![]() , it is observed that near the hot wall, the velocity increased as the anisotropic parameters of the porous medium
, it is observed that near the hot wall, the velocity increased as the anisotropic parameters of the porous medium ![]() and
and ![]() are made higher. Moreover, the curves show that the peak value of velocity increases rapidly near the hot wall as
are made higher. Moreover, the curves show that the peak value of velocity increases rapidly near the hot wall as ![]() or
or ![]() increases. Contrary to the following behavior, increasing values of these parameters contribute to slow the convective circulation along the warm wall as it is shown in Figure 3 when
increases. Contrary to the following behavior, increasing values of these parameters contribute to slow the convective circulation along the warm wall as it is shown in Figure 3 when ![]() for
for ![]() (
(![]() ), all curves sink in the neighborhood of the cold wall but the reversal flow is absent. We concluded that small values of anisotropic parameters of the porous medium contribute to stabilize the fluid motion.
), all curves sink in the neighborhood of the cold wall but the reversal flow is absent. We concluded that small values of anisotropic parameters of the porous medium contribute to stabilize the fluid motion.
Figure 5 shows the dimensionless temperature profile for mixed convection when ![]() for various values of the radiation parameter
for various values of the radiation parameter![]() . Curves plotted in Figure 5 reveal that the temperature decreases with an increase of
. Curves plotted in Figure 5 reveal that the temperature decreases with an increase of![]() . When
. When![]() , the temperature distribution is a function only of the ratio of wall temperature differences
, the temperature distribution is a function only of the ratio of wall temperature differences ![]() as predited by Aung and Worku [21] . Moreover, for all values of
as predited by Aung and Worku [21] . Moreover, for all values of![]() , the temperature is lower than that of the absence of thermal radiation. One can deduce that, the thermal radiation contributes to reduce the temperature
, the temperature is lower than that of the absence of thermal radiation. One can deduce that, the thermal radiation contributes to reduce the temperature
in the flow field when![]() . Increasing
. Increasing ![]() means that the release of the heat energy from the flow region and so the fluid temperature decreases.
means that the release of the heat energy from the flow region and so the fluid temperature decreases.
The effects of the anisotropic parameters of the porous matrix and the thermal radiation parameter on the gradient of the pressure are presented in Figure 6 and Figure 7 as a function of Darcy number ![]() when
when ![]() and
and![]() . From Figure 6 and Figure 7, it is noticed that, when
. From Figure 6 and Figure 7, it is noticed that, when ![]() is small enough
is small enough ![]() tends asymptotically toward a constant value that depend on
tends asymptotically toward a constant value that depend on ![]() and
and![]() . The limit
. The limit ![]() corresponds to a pure Darcy medium situation for which
corresponds to a pure Darcy medium situation for which ![]() given by Equation (62). In pure Darcy medium, the effects of both radiation and anisotropic parameters are observed to be significant. The increase of both of them diminishes the gradient of the pressure. This affects consequently the fluid motion and contributes to reduce the reversal flow as shown in Figure 2. We concluded that radiation effect contributes to stabilize the fluid motion. For example, when
given by Equation (62). In pure Darcy medium, the effects of both radiation and anisotropic parameters are observed to be significant. The increase of both of them diminishes the gradient of the pressure. This affects consequently the fluid motion and contributes to reduce the reversal flow as shown in Figure 2. We concluded that radiation effect contributes to stabilize the fluid motion. For example, when![]() , from Figure 6 when
, from Figure 6 when![]() ,
, ![]() and
and ![]() for
for
![]()
Figure 5. Temperature profile for mixed convection when ![]() for various values of the radiation parameter
for various values of the radiation parameter![]() .
.
![]() and Rd = 6 respectively. From Figure 7, for the same value of
and Rd = 6 respectively. From Figure 7, for the same value of![]() , when
, when![]() ,
, ![]() and
and ![]() for
for ![]() and
and ![]() respectively. As expected from equation 43, when the permeability of the porous medium
respectively. As expected from equation 43, when the permeability of the porous medium ![]() is increased, the boundary frictional resistance becomes gradually more important and adds to the bulk frictional drag induced by the solid matrix to slow the convection motion. As consequence, the effects of varying the values of the anisotropic parameters of the porous medium and the thermal radiation parameter become less and less important and the present solution approaches that for a pure viscous fluid indicated in Equation (42).
is increased, the boundary frictional resistance becomes gradually more important and adds to the bulk frictional drag induced by the solid matrix to slow the convection motion. As consequence, the effects of varying the values of the anisotropic parameters of the porous medium and the thermal radiation parameter become less and less important and the present solution approaches that for a pure viscous fluid indicated in Equation (42).
In Figure 8, the average wall friction ![]() is plotted as a function of
is plotted as a function of ![]() within the porous channel when
within the porous channel when![]() ,
, ![]() ,
, ![]() , and
, and ![]() for various values of
for various values of![]() . The results indicate that the average wall friction is enhanced when
. The results indicate that the average wall friction is enhanced when ![]() increased. It is observed that, when
increased. It is observed that, when ![]() is small enough,
is small enough, ![]() tends asymptotically toward a value that depends on
tends asymptotically toward a value that depends on ![]() and
and![]() . The limit
. The limit ![]() corresponds to a pure Darcy medium for which the average wall friction variation modeled by Equation (55). In this limiting case, the effects of
corresponds to a pure Darcy medium for which the average wall friction variation modeled by Equation (55). In this limiting case, the effects of
varying anisotropic parameters of the porous matrix are observed significant, since ![]() decreases as
decreases as ![]() is made larger. When the Darcy number is made large enough, the results indicate that the curves, for a given value of
is made larger. When the Darcy number is made large enough, the results indicate that the curves, for a given value of![]() , tend asymptotically toward the pure fluid situation (Equation (46)). The Darcy number required to reach this limit increases as the value of
, tend asymptotically toward the pure fluid situation (Equation (46)). The Darcy number required to reach this limit increases as the value of ![]() is made higher. For example, this happens at
is made higher. For example, this happens at ![]() when
when![]() , and
, and ![]() when
when![]() .
.
The effects of the radiation parameter Rd and the permeability ratio K* on the Nusselt number is illustrated in Figure 9 for Ra = 100, Da = 10−2, ![]() ,
, ![]() ,
, ![]() and
and![]() . It is observed that, for a given value of Rd, the convective heat transfer increases as Rd is made smaller. For a fixed value of Rd, Nu tends asymptotically toward a constant value as K* is made small enough
. It is observed that, for a given value of Rd, the convective heat transfer increases as Rd is made smaller. For a fixed value of Rd, Nu tends asymptotically toward a constant value as K* is made small enough![]() . As expected from Equation (80) predicting the
. As expected from Equation (80) predicting the
heat transfer for this limiting case, it is observed that ![]()
when![]() . These limits are indicated as dashed lines in Figure 9 for
. These limits are indicated as dashed lines in Figure 9 for ![]() and
and![]() . As it can be observed in Figure 9, the convection becomes less and less important as
. As it can be observed in Figure 9, the convection becomes less and less important as ![]() is made larger. Thus, for each value of
is made larger. Thus, for each value of ![]() considered in Figure 9, the heat transfer rate approaches the pure condition regime,
considered in Figure 9, the heat transfer rate approaches the pure condition regime, ![]() as
as ![]() is made large enough. The value of
is made large enough. The value of ![]() necessary to reach the pure condition regime depends upon
necessary to reach the pure condition regime depends upon![]() . For instance, for
. For instance, for![]() , pure condition is reached when
, pure condition is reached when ![]() while for
while for![]() ,
,![]() .
.
The influence of the anisotropic orientation ![]() on Nusselt number
on Nusselt number![]() , is presented in Figure 10 where the bounding walls are submitted to various values of the radiation parameter Rd and K* when
, is presented in Figure 10 where the bounding walls are submitted to various values of the radiation parameter Rd and K* when![]() ,
, ![]() , for
, for![]() ,
, ![]() ,
,![]() . We investigated cases where values of
. We investigated cases where values of ![]() for
for![]() .
.
Curves plotted in Figure 10 reveal a symmetry of the results with respect to![]() . It is observed that the heat transfer is enhanced with respect to that of an isotropic porous medium corresponding to
. It is observed that the heat transfer is enhanced with respect to that of an isotropic porous medium corresponding to![]() , when the
, when the
permeability ratio ![]() is made smaller than one (i.e.,
is made smaller than one (i.e.,![]() ). Moreover, for a given
). Moreover, for a given![]() , the higher heat transfer rate is obtained when
, the higher heat transfer rate is obtained when ![]() is smaller. For the range
is smaller. For the range ![]() and
and![]() , Figure 10 indicates that
, Figure 10 indicates that ![]() is minimum at
is minimum at ![]() for which permeability in vertical direction is minimum, but is maximum at
for which permeability in vertical direction is minimum, but is maximum at![]() . The inverse is observed for
. The inverse is observed for ![]() where the convective heat transfer is maximum at
where the convective heat transfer is maximum at ![]() and minimum at
and minimum at![]() . For a given
. For a given![]() , when
, when![]() ,
, ![]() is maximum (minimum) at
is maximum (minimum) at ![]() and minimum (maximum) at
and minimum (maximum) at![]() . The maximum (minimum) increased (decreases) when
. The maximum (minimum) increased (decreases) when ![]() is small (great) enough. Therefore, a maximum (minimum) convective heat transfer is reached when orientation of the principal axis with higher permeability of anisotropic porous medium is parallel (perpendicular) to the gravity. A Similar result has been obtained by Degan and Vasseur [17] while studying mixed convection through a vertical anisotropic porous channel with oblique principal axes.
is small (great) enough. Therefore, a maximum (minimum) convective heat transfer is reached when orientation of the principal axis with higher permeability of anisotropic porous medium is parallel (perpendicular) to the gravity. A Similar result has been obtained by Degan and Vasseur [17] while studying mixed convection through a vertical anisotropic porous channel with oblique principal axes.
5. Conclusions
A study has been made of mixed convection through a parallel-plate vertical porous channel submitted to a thermal radiative flux on its wall. The porous medium is assumed to be hydrodynamically anisotropic with its principal axes oriented in a direction that is oblique to the gravity.
Analytical expressions valid for fully developed flow and based on the generalized Brinkman-extended Darcy are obtained. The main conclusions of the present analysis are:
・ Both thermal radiation and anisotropic parameters have a strong influence on the fluid motion and the heat transfer through the parallel-plate vertical porous channel.
・ In the pure Darcy medium![]() , the velocity, the average wall friction, the pressure gradient and the heat transfer rates are similar to those given by a pure Darcy analysis. In this limit, the orientation angle of the principal axes of permeability and the permeability ratio and the thermal radiation parameter affect considerably the convection heat transfer.
, the velocity, the average wall friction, the pressure gradient and the heat transfer rates are similar to those given by a pure Darcy analysis. In this limit, the orientation angle of the principal axes of permeability and the permeability ratio and the thermal radiation parameter affect considerably the convection heat transfer.
・ In the fluid medium (![]() ), the resistance resulting from the boundary effects is predominant and adds to the bulk frictional drag induced by the solid porous matrix to slow down the convection motion. Thus, the effects of anisotropic parameters (i.e.,
), the resistance resulting from the boundary effects is predominant and adds to the bulk frictional drag induced by the solid porous matrix to slow down the convection motion. Thus, the effects of anisotropic parameters (i.e., ![]() and
and![]() ) and thermal radiation parameter
) and thermal radiation parameter ![]() on the convective heat transfer are progressively irrelevant, and the solutions obtained become independent of them.
on the convective heat transfer are progressively irrelevant, and the solutions obtained become independent of them.
・ The effects of increasing values of the anisotropic parameters and the thermal radiation parameter tend to decrease the temperature and the gradient of the pressure. Moreover, the decrease of values of thermal radiation reduces the fluid velocity and makes the reversal flow occurs.
・ For a given value of the thermal radiation parameter, a maximum (minimum) heat transfer rate through the parallel-plate vertical porous channel is obtained when the porous matrix is oriented in such a way that the principal axis with higher permeability is parallel (perpendicular) to the gravity.
NOTES
![]()
*Corresponding author.