Determination of Gamma Angular Distribution from the Shape of Spectral Line for the First Excited State of Carbon Nucleus ()
Received 27 November 2015; accepted 8 January 2016; published 11 January 2016
1. Introduction
Proton beam therapy is a high-quality radiation therapy which uses proton beam to irradiate neoplastic tissue. The main advantage of this type of radiotherapy is highly conformal dose deposition due to the presence of the Bragg peak. It allows depositing a maximum dose in the area of abnormal tissue while healthy tissues receive only a marginal dose [1] . However, if the range of protons in the patient’s body is not accurately known, then there is a risk of receiving an overdose by the organs at risk (OAR) or receiving an underdose by the treated volume (TV). To take a full advantage of the beneficial physical properties of the proton beam, it is often required to irradiate the tumor volume with a precision better than 1 - 2 mm, which means that proton therapy needs not only precise treatment planning but also monitoring and proton range verification during the treatment [2] . Monitoring of the proton range can be performed by detecting gamma rays produced in two kinds of nuclear reactions occurring in the patient’s body during the treatment: the production of positron-emitting isotopes and the excitation of the target nuclei by incident protons [1] .
Positron emission tomography (PET) is considered to be a feasible method of monitoring and verification the dose delivered during the proton therapy and currently it is the only technique of particle therapy monitoring in clinical application [3] . However, there are several limitations to this method, including the fact that energy deposition during proton therapy mismatches the production of positron-emitting isotopes and the appearance of biological washout effects related to blood perfusion and metabolism. Furthermore, it has been observed that delay between treatment and taking PET scan affects determination of the range due to different half-lives of isotopes [2] . This issue can be overcome by real-time PET monitoring procedure, which is currently a subject of studies [4] . Nevertheless, comparison of PET images and Monte Carlo simulations can reveal the range more accurately [2] .
Due to numerous drawbacks of PET dose monitoring, new and more effective solutions have been searched for. The approach based on the measurement of prompt gamma radiation seems to be among the most promising options. Prompt gamma radiation is produced in various interactions of a proton beam with the target nuclei e.g. inelastic scattering and excitation. Its emission takes place within less than one nanosecond after nuclear reaction and indicates the place of nuclear interactions; therefore it allows monitoring beam range in real time [3] . Gamma quanta created from deexcitation of excited states of 12C and 16O carry energy of several MeV. As they interact rather weakly with human tissue, they bear almost undisturbed information.
The work presented in this article is part of the project Investigation of gamma emission in experimental modeling of hadron therapy, which aims to examine correlation between the characteristics of the gamma radiation emitted during proton therapy and the Bragg peak position. Research conducted within the project includes experiments designed to simulate course of the proton therapy as well as Monte Carlo simulations.
This paper presents analysis of experimental data with regards to the position and shape of the carbon line stemming from deexcitation of the first excited state of carbon nuclei. Mathematical model describing the shape of the carbon spectral line has been developed in order to reproduce experimental data, which allowed reconstructing angular distribution of the nuclear process occurring in patient’s body during treatment.
2. Experimental technique
A series of measurements were carried out in Cyclotron Centre Bronowice, Cracow, Poland in order to obtain data on gamma-emission from the interaction of proton beam with phantoms of the elemental composition simulating human tissue. The experimental conditions were designed to deliver data useful for hadron radiotherapy. The proton beam with energy of 70 MeV was accelerated in the Proteus C-235 cyclotron. Figure 1 shows schematically the experimental setup. Intensity of the beam was controlled using a Beam Current Monitor (BCM) (1) in form of a pair of telescopes made of plastic scintillators. The telescopes registered protons scattered (2) on the titanium exit window of the beam pipe (3) with the rate proportional to the intensity of the beam. The data registered by BCM was used for relative normalization of obtained gamma spectra.
The phantom with adjustable thickness (thick phantom) (4) and an additional thin target of the same material and fixed thickness (5) were placed on the beam path (6). Two materials of phantoms were investigated so far: poly(methyl methacrylate) PMMA (C5O2H8)n with density of 1.19 g∙cm−3 and graphite with density of 1.74 g∙cm−3.
The gamma rays were detected using two HP Ge detectors with anti-Compton shielding (7). The detectors were mounted on movable platforms, which allowed to register gamma spectra at different angles for different
![]()
Figure 1. Scheme of experimental setup (not to scale). 1―beam current monitor, 2― scattered protons, 3―window of the beam pipe, 4―thick target (variable thickness), 5―thin target (fixed thickness), 6―beam path, 7―HP Ge detectors with anti-Comp- ton shielding, 8―lead shielding. Data presented in the article were registered from the highlighted part of the setup.
measurement series. Each of the detectors was collecting data from different parts of the experimental setup: first one from the thick phantom, and second one from the thin target. This configuration of detection system enables an integrated gamma emission study along with a differential measurement. Additionally, lead walls (8) were placed as shown in Figure 1, in order to shield detectors from radiation emitted from the other target (the one that the detector was not directed onto).
The parameters which were fixed during a single measurement series were the following: proton beam energy, detection angle and phantom material, while the variable parameter was the phantom thickness. Change of the thick phantom thickness during a measurement series allows modifying average proton energy inside the thin target in small, precise steps.
Experimental data presented in this paper were obtained in measurements with graphite targets and a HP Ge detector placed at 90˚ to the beam direction, collecting data from the thin target. Thick target thickness has been changed from 15 mm up to 30 mm which resulted in average proton energy inside the thin target changing from 41.16 MeV till complete stopping of proton beam. Average energy was estimated with Geant4 simulation, as the mean value of the energy distribution for those protons passing the thin target, which were still able to excite the 4.44 MeV carbon state.
3. Shape of the 12C4.44→g.s. line―The Model
The 12C4.44→g.s. line is visible in the obtained gamma spectra as a double peak (Figure 2). The explanation of its shape lies in the interplay of the Doppler shift and the selective population of magnetic sublevels of the first excited state of carbon nuclei in the inelastic scattering process [5] . This phenomenon has been also observed in the gamma spectra registered from solar flares and molecular clouds [6] .
The interaction between target nuclei and incident protons occurs in two stages (Figure 3). In the first step incident proton causes excitation of the target nucleus [5] . Angular distribution in the centre-of-mass for this process is typically presented in the basis of Legendre polynomials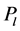 
as follows:
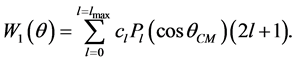(1)
The coefficients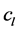 
have been calculated for each studied proton energy using the TALYS package [7] .
In the second step, deexcitation of the excited nucleus occurs along with the emission of the gamma quantum. Angular distribution of this process in the rest frame of the excited carbon nucleus is given by:
![]()
Figure 2. Typical gamma spectrum registered from the thin target in described experimental conditions. Average energy of protons inside the thin target was 16.13 MeV.
![]()
Figure 3. The scheme of two-step reaction of protons interacting with matter. Step I: excitation of 12C nucleus, step II: deexcitation of the excited state with emission of gamma quantum.
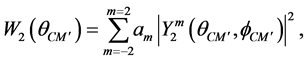(2)
where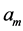 
is probability for populating the m sublevel and 
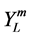are spherical harmonics, where the choice of 
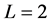is given by the difference of spins of excited and ground states. In the performed calculation, as a quantization axis a normal to the scattering plane has been chosen [5] . Coefficients 
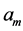are unknown and they are calculated based on the experimental data. Due to holding following constraints:
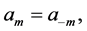(3)
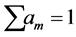(4)
it is sufficient to determine only two of them (e.g.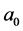 
and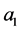
) to fully describe angular dependence of the 12C4.44→g.s. transition [6] .
4. Results
Model calculations were carried out using ROOT data analysis framework [8] . For both reaction stages the products are generated uniformly in the respective phase spaces and the corresponding probabilities ![]()
and ![]()
are calculated based on the angles and assumed values of parameters ![]()
and![]()
. Subsequently, the product of those is used as a weight for each event. Model calculations account also for the finite size of the detector and its position as well as for the energy resolution of the detector estimated independently as FWHM of oxygen 6.13 MeV line, visible in the spectra obtained in measurements with a PMMA phantom.
Values of ![]()
and ![]()
coefficients have been determined by comparing experimental data on the 12C4.44→g.s. line shape with theoretical model and constructing map of ![]()
distribution for all possible combinations of searched parameters. For a certain choice of parameters ![]()
and![]()
, a theoretical line shape is determined, and a ![]()
for that and the experimental data is calculated as follows:
![]()
(5)
where, ![]()
is experimental value, ![]()
is theoretical value calculated based on the model, ![]()
and ![]()
are respective uncertainties of those. The sum is calculated for n bins in the studied energy interval. Typical ![]()
distribution is shown in Figure 4. The triangle indicates area, where ![]()
and ![]()
coefficients have physically valid values, which is a consequence of (4). However, maps were constructed in a wider range to enhance the visibility of the minimum in those distributions and make determination of its position more precise. Values of ![]()
and ![]()
parameters are found as coordinates of the minimum of the ![]()
distribution map. The cross on the ![]()
distribution map (Figure 4) indicates the determined position of the minimum. Such ![]()
distribution maps were calculated for each studied energy of protons inside the thin target, which allowed to determine values of ![]()
and ![]()
parameters for them. Values of ![]()
and ![]()
parameters determined for the analysed data series are shown in Figure 5 as a function of protons energy.
Figure 6 sets together theoretical line shape (calculated according to described model and with values of ![]()
and ![]()
determined as above) and the experimental data. Additionally, known parameters ![]()
and ![]()
fix the shape of the angular distribution of the reaction (Figure 7).
![]()
Figure 4. Typical map of χ2 distribution. The triangular shape indicates area, where a0 and a1 coefficients have physically valid values and red cross indicates the position of the minimum. Map has been constructed for mean proton energy in the target of 16.13 MeV (preliminary results).
![]()
Figure 5. Values of a0 and a1 parameters as a function of protons energy (prelimi- nary results).
![]()
Figure 6. Comparison of the shape of experimental 12C4.44→g.s. line and theoretical line reconstructed based on mathematical model (preliminary results). Presented errors are purely statistical.
![]()
Figure 7. Angular distribution (not normalized absolutely) of gamma emission in 12C4.44→g.s., as determined based on a0 and a1 parameters calculated for proton energy of 16.13 MeV (preliminary results).
5. Summary and further research
Mathematical model describing the shape of the 12C4.44→g.s. transition line has been developed in order to reproduce experimental data obtained in the measurements simulating the course of the proton therapy. As a result of model calculations, the values of parameters ![]()
and ![]()
were obtained. Those allow to fully reconstruct the shape of the carbon line as well as determine the angular distribution of the C*(4.44 MeV) deexcitation―a nuclear reaction occurring during proton therapy in patient’s body. The elaborated method allows extracting full angular distribution of the process merely from the shape of the spectral line measured at a single detection angle. Further plans comprise measurements for beam energy of 150 MeV and 230 MeV, which will cover full range of energy used in proton therapy, and also at various polar angles. The latter will enable a comparison of the model calculations with classical measurement of the angular distribution and thus will provide a rigorous test of the model.
Acknowledgements
Research was conducted in collaboration with the Institute of Nuclear Physics of the Polish Academy of Sciences and RWTH Aachen University.
The project Investigation of gamma emission in experimental modeling of hadron therapy is carried out within the POMOST programme of the Foundation for Polish Science, co-financed from the European Union under the European Regional Development Fund.
NOTES
![]()
*Corresponding authors.