Group-Invariant Solutions for the Generalised Fisher Type Equation ()
Received 30 October 2015; accepted 27 December 2015; published 30 December 2015

1. Introduction
In this paper, the focus is on the generalised Fisher type equation arising in population dynamics. The analysis of the generalised Fisher equation has been carried out using Lie point symmetries (see e.g. [1] ) and construction of conservation laws see e.g. [2] ). These types of equations have appeared in many fields of study, for example, the reaction-diffusion equations arise in heat transfer problems [3] , biology [4] [5] , and transmission of nerve signals [6] . The reaction-diffusion equations such as the generalized Fisher equation describe how the concentra- tion of a substance is distributed in space changes, whereby the diffusion term causes the spread over the surface. Fisher [4] had used a nonlinear reaction-diffusion equation to model the population growth of mutant genes over a period of time. One can take Fisher’s equation [4] and with simple modifications, and can derive the Fitzhugh- Nagumo equation [7] . Moreover, one can make a modification to the Fitzhugh-Nagumo equation in order to obtain Huxley’s equation [4] .
A significant amount of work has been done in the process of studying the reaction-diffusion equations. In particular, from the classical Lie symmetry analysis point of view (see e.g. [8] ), and nonclassical symmetry techniques [7] [9] [10] . It turns out that reaction diffusion equations such as the generalised Fisher equation admit the genuine nonclassical symmetries if the source term is given by a cubic (see e.g. [7] [10] ). In a recent work [3] [11] , the authors assume a diffusivity which depends on space variable. In this case, the diffusivity may be given as a power law function of space variable for the given reaction-diffusion equation to admit non- classical symmetries.
This paper is arranged as follows. In Section 2, we provide the mathematical models for problems arising in population dynamics. In Section 3, we provide a brief account of the symmetry methods. In Sections 4 and 5, we provide the nonclassical and classical Lie point symmetry reductions, respectively. In Section 6, we briefly provide remarks on the conservation laws of the equation in question. The discussions and concluding remarks are given in Section 7.
2. Mathematical Description
For a diploid population having two available alleles at the locus in question (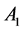 and
and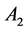 ), there are three possible genotypes;
), there are three possible genotypes;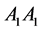 ,
, 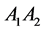 and
and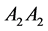 , where
, where 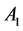 is the allele is under observation. Then, the following three equation describe the change in the genotype frequencies
is the allele is under observation. Then, the following three equation describe the change in the genotype frequencies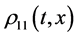 ,
, 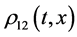 and
and ,
,
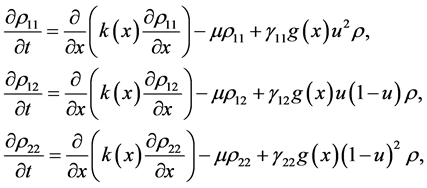 (1)
(1)
where 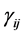 are the reproductive success rate of genotype
are the reproductive success rate of genotype 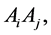
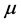 is the common death rate,
is the common death rate,  is the total population density,
is the total population density,  , and u is the frequency of allele
, and u is the frequency of allele![]() . The frequency of allele
. The frequency of allele ![]() is given by
is given by![]() . Note that u depends on t and x. The frequency of allele
. Note that u depends on t and x. The frequency of allele ![]() is
is
![]() (2)
(2)
Differentiating Equation (2) with respect to t, then the three genotype equations (1) collapse into a single equation that describes the change in frequency of the new mutant gene
![]() (3)
(3)
where ![]() and
and![]() . Equation (3) is a reaction-diffusion-convection equation with cubic nonlinearities referred to here as a generalised Fisher equation. If
. Equation (3) is a reaction-diffusion-convection equation with cubic nonlinearities referred to here as a generalised Fisher equation. If![]() , the total population density is
, the total population density is
constant in space, Equation (3) reduces to the Fitzhugh-Nagumo equation. When deriving the models with the continuous method, there is an extra convective term due to the assumption that total population density is not uniform spatially.
If one is to consider the conditions that Fisher had examined, so that the allele in question is completely recessive. This implies that the genotypes ![]() and
and ![]() have the same phenotype, therefore they have the same reproductive success rate. Let the alleles represented by A and a be set as the alleles
have the same phenotype, therefore they have the same reproductive success rate. Let the alleles represented by A and a be set as the alleles ![]() and
and ![]() respectively. Hence,
respectively. Hence, ![]() is the allele under consideration. If
is the allele under consideration. If ![]() the one obtains
the one obtains
![]() (4)
(4)
where![]() . One can see that Equation (4) is also a reaction-diffusion-convection equation. If
. One can see that Equation (4) is also a reaction-diffusion-convection equation. If![]() , then Equation (4) reduces to a generalized Fisher type equation,
, then Equation (4) reduces to a generalized Fisher type equation,
![]() (5)
(5)
which models the propagation of impulses along nerve axons. In this paper we focus on the reaction diffusion equation of the form
![]() (6)
(6)
We refer to Equation (6) as the governing equation. The variable u may be viewed as representing population. The diffusivity ![]() may be given by quadratic in x for equations such as Equation (6) to admit genuine nonclassical symmetries (see e.g. [3] [11] ). In this paper the coefficient of the cubic source term
may be given by quadratic in x for equations such as Equation (6) to admit genuine nonclassical symmetries (see e.g. [3] [11] ). In this paper the coefficient of the cubic source term ![]() is given by the power law
is given by the power law ![]() where n is a real constant.
where n is a real constant.
3. Symmetry Methods for Differential Equations
In this section, we restrict discussions to symmetry analysis of second order differential equations. Given for example, a second order differential equation of the form
![]() (7)
(7)
where the subscripts denote all possible first and second derivatives of u with respect to t and x. Finding classical Lie point symmetries of Equation (7) implies seeking infinitesimal transformations of the form
![]() (8)
(8)
generated by the vector field
![]() (9)
(9)
Note that the transformations in (8) are equivalent to the one-parameter Lie group of transformations that leaves the Equation (7) unchanged or invariant. The action of X is extended to all derivatives appearing in the equation in question through the appropriate prolongation. The infinitesimal criterion for invariance of the given equation is given by
![]() (10)
(10)
Equation (10) yields an overdetermined system of linear homogeneous equation which can be solved algorithmically. Note that the solution of Equation (10) yield the classical Lie point symmetries admitted by Equation (7). Full theory of determination of Lie point symmetries may be obtain in among other texts [12] - [14] . If the invariance is sought subject to a further constraint
![]() (11)
(11)
known as the invariant surface condition (ISC), that is given
![]() (12)
(12)
then one obtain a system of nonlinear determining equations which may yield the nonclassical symmetry generators [15] .
4. Nonclassical Symmetry Reductions
In this section, we consider nonclassical symmetry reductions of the generalised Fisher type equation given in Equation (6). Here, ![]() is given as a cubic function of u (see e.g. [7] ) and both the diffusivity and the coefficient of the source term are given by power law functions of the space variable.
is given as a cubic function of u (see e.g. [7] ) and both the diffusivity and the coefficient of the source term are given by power law functions of the space variable.
4.1. Nonclassical Symmetry Reduction Given n = 1
In this subsection, we consider Equation (6) with ![]() and
and ![]() Assuming
Assuming![]() , the infinitesimal criterion for invariance of the form (12) results in a system of overdetermined nonlinear determining equations which is split in the powers of in powers of
, the infinitesimal criterion for invariance of the form (12) results in a system of overdetermined nonlinear determining equations which is split in the powers of in powers of ![]() as given below;
as given below;
1:
![]()
![]() :
:
![]()
![]() :
:
![]()
![]() :
:
![]()
The solution of these determining equations yields the admitted nonclassical symmetry generator given by
![]() (13)
(13)
The associated ISC is given by
![]() (14)
(14)
Using governing equation and the ISC (14) simultaneously one may eliminate ![]() to get the equation
to get the equation
![]() (15)
(15)
Employing a change of variables ![]() then Equation (15) reduces to
then Equation (15) reduces to
![]() (16)
(16)
We introduce the “modified” Hopf-Cole transformation given by
![]() (17)
(17)
to simplify Equation (16). Upon substituting (17) into Equation (16), it turns out that ![]() must satisfy an algebraic equation
must satisfy an algebraic equation
![]() (18)
(18)
Hence
![]()
and so Equation (16) transforms to a linear third ODE
![]() (19)
(19)
The solution to Equation (19) is given by
![]() (20)
(20)
Substituting backwards for![]() , produces
, produces
![]() (21)
(21)
Solving for the arbitrary functions, ![]() , Equation (21) is substituted back into the ISC given by Equation (14). Hence, we obtain in terms of the original variables the general nonclassical symmetry exact solution given by
, Equation (21) is substituted back into the ISC given by Equation (14). Hence, we obtain in terms of the original variables the general nonclassical symmetry exact solution given by
![]() (22)
(22)
where ![]() and
and ![]() are arbitrary constants. Solutions (22) is depicted in Figures 1-3.
are arbitrary constants. Solutions (22) is depicted in Figures 1-3.
![]()
Figure 1. Population frequency over time and space given solution (22). Here, the parameters are given by![]()
![]()
Figure 2. Population dynamics as time progresses over space given solution (22). Here, the parameters are given by![]()
![]()
Figure 3. Impact on the population frequency as time evolves given solution (22). Here, the parameters are given by![]()
If the source term is given by ![]() then
then![]() , gives rise to the equation
, gives rise to the equation
![]() (23)
(23)
In this case, the exact (group-invariant) solution will be given by,
![]() (24)
(24)
4.2. Nonclassical Symmetry Reduction Given n ¹ 1
Suppose that one considers a more general case, ![]() where
where![]() . The governing equation then becomes
. The governing equation then becomes
![]() (25)
(25)
Following the steps above, the admitted genuine nonclassical symmetry is given by
![]() (26)
(26)
The associated ISC is given by
![]() (27)
(27)
Eliminating ![]() using (25) and (27) one obtains
using (25) and (27) one obtains
![]() (28)
(28)
Introducing the transformation ![]() yields
yields
![]() (29)
(29)
In this case, it turns out that the “modified” Hopf-Cole transformation should be given by
![]()
as such the transformed Equation (29) becomes a solvable linear third order ODE
![]()
In terms of the original variables the exact solution is given by
![]() (30)
(30)
where ![]() are arbitrary functions of t. Without loss of generality, set
are arbitrary functions of t. Without loss of generality, set ![]() and then solving for the rest of the arbitrary functions by substituting Equation (30) into the ISC corresponding to this case. Then,
and then solving for the rest of the arbitrary functions by substituting Equation (30) into the ISC corresponding to this case. Then, ![]() and
and ![]() can be found to be
can be found to be
![]() (31)
(31)
or
![]() (32)
(32)
and
![]() (33)
(33)
If![]() , then the problem is equivalent to the one considered in [3] and
, then the problem is equivalent to the one considered in [3] and ![]() yields the problem discussed in the previous section.
yields the problem discussed in the previous section.
5. Classical Lie Point Symmetry Reductions
5.1. Classical Lie Point Symmetry Reductions Given n = 1
We consider the case where ![]() and
and ![]() in Equation (6). In this case the admitted Lie algebra is three dimensional and spanned by the vector fields
in Equation (6). In this case the admitted Lie algebra is three dimensional and spanned by the vector fields
![]()
![]()
![]()
It is easy to show that this Lie algebra is closed. Reductions are possible by any linear combination of these symmetries. Usually one may determine the optimal system of subalgebras of these classical Lie point symmetries to determine reductions which are not connected by any point transformation. However here we restrict analysis to three cases only. Note that symmetry generator ![]() led to hard to solve reductions and thus its use is omitted.
led to hard to solve reductions and thus its use is omitted.
5.1.1. Reduction by X2
The corresponding characteristic equations corresponding to this scaling symmetry are given by
![]() (34)
(34)
and the functional form of thew group-invariant solutions is given by
![]() where f satisfies the ODE
where f satisfies the ODE![]() (35)We obtain
(35)We obtain![]() (36)and so, the group-invariant solution for the governing equation is given by
(36)and so, the group-invariant solution for the governing equation is given by![]() (37)The solution in Equation (37) is depicted in Figure 4 and Figure 5. Given the source term
(37)The solution in Equation (37) is depicted in Figure 4 and Figure 5. Given the source term![]() , with k being an arbitrary constant we obtain
, with k being an arbitrary constant we obtain
![]()
Figure 4. Impact on the population frequency over time and displacement given solution (37). Here,![]()
![]()
Figure 5. Impact on the population frequency given solution (37). Here, ![]() and
and![]() .
.
![]() (38)
(38)
The transformation, ![]() can be made to Equation (38) to give
can be made to Equation (38) to give
![]() (39)
(39)
In terms of the original variables the exact (group-invariant) solution for Equation (38) is given by
![]() (40)
(40)
5.1.2. Reduction by X1
The time translation symmetry leads to the steady state problems with the model given by the modified Emden- Fowler equation of the form
![]() (41)
(41)
The transformation ![]() reduces the ODE (41) into the Emden-Fowler equation
reduces the ODE (41) into the Emden-Fowler equation
![]()
which is hard to solve exactly. Note that ODE (41) admits the scaling symmetry which may be used to reduce the order this equation by one.
5.1.3. Reduction by the Combination ![]()
To construct the exact (group-invariant) solution we consider the linear combination of symmetries ![]() and
and ![]() The characteristic equation corresponding to this combination is given by
The characteristic equation corresponding to this combination is given by
![]()
The basis of invariants is given by
![]()
and
![]()
Let ![]() and
and ![]() Thus the functional form of the group-invariant solution is given by
Thus the functional form of the group-invariant solution is given by
![]() (42)
(42)
where F satisfies the second order ODE
![]() (43)
(43)
Equation (43) admits the following rotation symmetry,
![]() (44)
(44)
We implement the method of differential invariants to reduce the order of Equation (43) by one. The first prolongation of X is given by
![]() (45)
(45)
The characteristic equations are given by,
![]() (46)
(46)
The invariants are therefore, ![]() and
and![]() . Writing
. Writing ![]()
![]() and
and ![]() we obtain the reduced equation
we obtain the reduced equation
![]() (47)
(47)
A further simplification can be made to Equation (47), whereby![]() . Therefore Equation (47) can be written as,
. Therefore Equation (47) can be written as,
![]() (48)
(48)
Suppose![]() , then Equation (48) becomes variable separable and the solution for
, then Equation (48) becomes variable separable and the solution for ![]() can be found. Substituting back for G gives,
can be found. Substituting back for G gives,
![]() (49)
(49)
wherein an integration constant vanished for simplicity.
In terms of the original variables we obtain a group-invariant (particular) solution given by
![]() (50)
(50)
where ![]() is an arbitrary constant. The ODE (47) is difficult to solve exactly when
is an arbitrary constant. The ODE (47) is difficult to solve exactly when![]() . Solution (50) is depicted in Figure 6.
. Solution (50) is depicted in Figure 6.
5.2. Classical Lie Point Symmetry Reduction Given n ¹ 1
In this case, Equation (25) admits a two dimensional Lie symmetry algebra spanned by the base vectors
![]()
Figure 6. Impact on the population frequency given solution (50). Here,![]()
![]()
![]()
5.2.1. Reduction by X1
The time translation led to the steady state problem given by the Emden-Fowler type ODE
![]()
Which is harder to solve exactly.
5.2.2. Reduction by X2
Reduction by this symmetry generator led to a functional form of the group-invariant solution given by
![]()
which is in fact separation of variables. Here F satisfies the first order ODE
![]()
which has a solution
![]()
where ![]() is an integration constant. Thus we obtain
is an integration constant. Thus we obtain
![]()
6. A Note on Conservation Laws of Equation (25)
It is worth noting that Equation (25) has the conservation laws given by the conserved vectors
![]()
![]()
provided ![]() which implies a linear heat equation with spatial dependent diffusion term. These combination of conserved vectors is obtained by both direct and multiplier methods.
which implies a linear heat equation with spatial dependent diffusion term. These combination of conserved vectors is obtained by both direct and multiplier methods.
7. Some Discussions and Concluding Remarks
In this paper, we have used both classical and nonclassical symmetry methods to construct the exact solutions. Some new group-invariant (exact) solutions for reaction diffusion equation with spatially dependent diffusivity and the coefficient of the source term have been constructed using both classical and nonclassical symmetry techniques. Figures 1-6 depict the change in mutant population with respect to either time or space or both. The effects of the parameters appearing in the plotted exact solutions on the population are displayed. We have introduced the modified Hopf-Cole transformation to transform a nonlinear second order ODE to a simpler to solve linear third order ODE. To the best of our knowledge, this transformation has never been used in the recorded literature.