Received 2 October 2015; accepted 22 December 2015; published 25 December 2015
1. Introduction
Graphene is a monolayer of carbon atoms tightly packed into a two-dimensional (2D) honeycomb lattice. Since its discovery in 2004, graphene has attracted a great deal of attention mainly due to its exceptionally high crystal and electronic quality. Shear viscosity has been studied in graphene [1] [2] . The shear viscosity establishes transverse velocity gradients that obstruct coherent electron flow. Under some conditions, one has relativistic particles in graphene forming a quantum Hall fluid; a strongly correlated sates of matter, which flows just like fluid and without such shearing resistance or dissipation. The viscosity measured in the quantum Hall fluid is what is termed Anomalous (also called Hall or dissipationless) viscosity [3] . Quantum fluids are particularly interesting especially due to the remarkable natural phenomenon occurring in superconductivity, superfluidity, ultracold atoms. Fractional Quantum Hall (FQH) Effect is yet another example. The ground states of FQH states are holomorphic in nature and gapped. These gapped states are characterized by a universal anomalous viscosity. The viscosity is revealed when stress tensor becomes sensitive to stress preserving deformations of the fluid. In this context, the origin of the anomalous term is due to fluid velocity diverging at microscopic scale which deforms a metric locally and causes dilatation of particle coordinates. The divergences due to individual particles are collectively manifested at macroscopic scale as an anomalous term. Another important term arising from metric deformations at finite temperature is Hall expansion coefficient. It is well established that graphene can respond to local deformations by producing strain which in turn induces giant pseudo-magnetic fields as much as 10 T in strained graphene [4] and 300 T in graphene nanobubbles [5] . The induced field allows vortices in the system to feel an effective magnetic field. It is the Hall expansion coefficient that captures the contribution.
Recently, there has been a great deal of interest and renewed focus on the anomalous viscosity,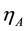 
of quantum fluids. In particular, a universal relation 
for FQH states of generic bulk systems was obtained [6] by studying the response to metric deformations, where 
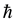is plank constant, 
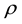is fluid density and 
is so called shift of FQHS. In [7] ,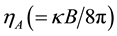 
was obtained for the FQH states of relativistic particles in graphene by electromagnetic and gravitational response, where 
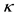is the relativistic analogue of
. The same general result, including anomalous term, was also obtained by Abanov within effective hydrodynamic theory [8] and within Euler vortex hydrodynamics [5] . However, all these results lack finite temperature effects which can have remarkable consequence on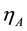 
and other transport properties.
In the following, we consider flows of quantized Hall vortices in the graphene Hall fluid as elementary objects forming themselves a highly correlated quantum fluid. In the regime of long-wave slow motion, an accurate hydrodynamic description becomes possible and does, in its own validity, not depend on the microscopic behavior of the electronic fluid. Vortex-vortex interactions will then be responsible for appearance of vortex FQH Effect. The hydrodynamics of vortex matter presented here differs from Euler hydrodynamics [9] by an anomalous term. Within this many-vortex approach, the anomalous term has been derived for bulk single component non-degenerate systems [5] without the Hall expansion coefficient.
The remaining of the paper is organized as follows. In Section 2 we obtained vorticity equation from Euler hydrodynamic equation for graphene. From the Euler equation, we obtained a quantized Helmholtz-Kirchoff vortex solution. Vortex flux and momentum conservation laws are subsequently derived. The stress tensor is deduced from which the anomalous viscosity is read off. In Section 3, we analyzed behavior of the anomalous viscosity under density and temperature profiles for different filling fractions of the quantum hall vortex fluid. We made comparisons of our results to some recent experimental findings of FQHE energy gaps and concluded in Section 4 highlighting possible applications of the results.
2. Theory
2.1. Euler Hydrodynamics and Point Vortices
Two dimensional Euler hydrodynamics can be straightforwardly derived following Boltzmann transport equation at local equilibrium [10] . Particle distribution is reduced to continuity and Euler equations for density and momentum
(1)
respectively. Where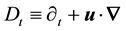 
and 
is macroscopic fluid velocity connected with the microscopic electron velocity,
. p is the partial pressure per density and ![]()
is the fluid component index. For graphene,![]()
. ![]()
and ![]()
are the valley and spin indexes, respectively. Taking the curl of the Euler Equation (1), we get
![]()
(2)
where the quantity, ![]()
is vorticity which is non-zero for rotational incompressible flows. ![]()
is considered as frozen into the fluid and constitute its own fluid. The continuity equation for the vortex fluid![]()
, also holds. A solution for Equation (2) exists and consists of point-like vortices. The fluid velocity is
![]()
(3)
where![]()
, ![]()
, ![]()
is the circulation of ![]()
vortex belonging to fluid component![]()
, and ![]()
which is identified with cyclotron frequency of the fluid particles. Assuming a flow in which the circulation, ![]()
is both minimal and chiral so that in the limit, ![]()
rotation is compensated by the large number of vortices. If magnetic field is present, the vortices of all components are smoothly distributed with fixed
mean density,![]()
. Borhn-Sommerfeld phase-space quantization leads to quantization of the
circulation![]()
. Where ![]()
is inertia vortex flow and ![]()
is an integer. The equation for the slow motion of vortices is easily obtained from Equation (3). It is given by
![]()
(4)
Equation (4) is the Helmholtz-Kirchoff equation for vortices. We will specialize in the zero energy state of the system where ![]()
and ![]()
components of the fluid decouple. Dynamics are then localized in either sublattice and the ![]()
dependence may be dropped.
2.2. Temperature Effect on Dynamics of Hall Vortices and Viscosity Anomaly
In the quantum Hall regime of dissipationless flow, fluid particles do not carry heat flux, but vortices do. Vortices move in response to temperature gradient,![]()
. This can be captured in a vortex density defined through momentum flux as
![]()
(5)
Using the identity ![]()
and the ward identity
![]()
[5] in Equation (5), we get
![]()
(6)
Equation (6) is crucial in these studies. In particular, our results are based on the second term which dictates discussions that follows. The term is responsible for anomalous behavior of the fluid when approaching a vortex. It is a quantum or micro-scale phenomenon which manifests itself at classical regime due to possible broken translation symmetry associated with lattice scale deformations. Its presents renormalize the vortex-vortex interactions in Equation (4). It also creates stresses perpendicular to the fluid flow with no work or dissipation. The associated transport coefficient (viscosity) is expected to be dissipationless. The momentum conservation following from broken translation invariance in the presence of external forces yields
![]()
(7)
where the stress tensor is ![]()
and![]()
. ![]()
is the external force. The kinetic coefficient ![]()
is the anomalous (dissipationless) viscosity. Except for the temperature dependence, the dessipationless viscosity has the same structure as the universal relation obtained in literature for graphene Fractional quantum Hall states [7] . i.e.,
![]()
(8)
In order to have a complete description of our system, one need to quantize Equation (6). The process physically leads to interpretation of the quantized circulation as the filling factor of the fractional vortex Hall states [5] . A connection between ![]()
and the so called shift, ![]()
of a Hall state is easily established. For
Graphene,![]()
. Except for the re-definition of![]()
, the quantized vortex velocity assumes the
same form as Equation (6). Taking the curl and utilizing the relation![]()
, we have
![]()
(9)
2.3. Effective Magnetic Field
As we have pointed out in the introduction, geometric deformations can lead to induction of giant synthetic magnetic fields. Vortices feel this contribution in addition to external magnetic field as an effective field, ![]()
The anomalous viscosity for the graphene-vortex system takes the shape, ![]()
with ![]()
and![]()
. The Fourier transform of ![]()
in time-domain yields frequency-dependent viscosity
![]()
(10)
where![]()
. To compute![]()
, we decomposed it into![]()
. ![]()
is the applied field. First we need to compute ![]()
from Equation (9). To do that, we require that in the ground sate ![]()
which yields![]()
. Expanding ![]()
in small temperature gradients to get an iterative expression for the magnetic field,
![]()
(11)
where ![]()
is the anomalous term. The Hall expansion coefficient is defined as ![]()
The minus sign is inferred from recent experimental results on graphene at low-temperatures [11] -[14] . Because strain in graphene induces giant synthetic magnetic fields, at finite temperatures ![]()
can have great consequences on the system’s electronic transport properties. Thus, the coefficient can characterize stress and knowing it can be very critical in strain engineering. In Equation (11) and throughout the work we used a Gaussian profile for the temperature.
Finally, to obtain ![]()
we recall that the Magnus force acting on vortices has the form
![]()
(12)
The term in brackets is written in such a way that the force stays constant in order that fluctuations in the zero energy states are bounded. Replacing v in Equation (12) and using ![]()
up to leading order in gradient expansion, we get
![]()
(13)
3. Results and Discussion
We now discuss the behavior of anomalous viscosity. Here, we observed how small temperature gradients affect viscosity of vortex fluid quantized on Hall states having filling fraction within![]()
.
In Figure 1, we first simulate viscosity for different filling fractions with the intention to associate detectability of a fraction to the viscosity. The observation is motivated by the fact that some ![]()
-values are generally strong and are easily seen in quantum hall experiments. We noticed deviation of the ![]()
-curves from some mean viscosity, ![]()
(not shown in either plots) which passes through the ![]()
(red) line close to its mid-point. The positive and negative signs are for the left and right plots in the figure. The amount of deviation measures the strength of (ability to observe) a Hall state. Thus from Figure 1, it is clear that both ![]()
and ![]()
give the highest deviations which collaborate experimental results [15] [16] . The negative sign is crucial and may suggest the weak observation of these filling fractions in experiments.
In Figure 2, we observe the anomalous viscosity over varying temperature, T. At some critical values, ![]()
, the viscosity grows to positive and negative infinities for ![]()
and![]()
, respectively. Figure 2(c) and Figure 2(d) was similarly obtained for fractions within![]()
. Above and below![]()
, ![]()
is robust (flat). This particular character places graphene as an important industrial material where temperature and viscosity are of utmost importance.
In Figure 3, we plotted ![]()
in the neighborhood of infinites initially excluded from Figure 2. We extracted the critical temperatures ![]()
giving rise to anomalous viscosity infinities, ![]()
and study ![]()
behavior as shown in Figure 4. The following characterized the appearance of observed temperature continuums in the plot. The wider empty spaces, which enclose critical temperatures at which fractional fillings are observed, mean several new fractions are more likely to be found within the respective regions. However, experiments are limited in their ability to observe many of these fractions. It is no surprise that current experiments are still reporting newer fractions [15] [16] . In fact, to explain the hidden fractions from experiments, we provide a physical meaning to the infinities in the anomalous viscosity which should connect well with experiments. We interpret ![]()
as a measure of device sensitivity which in turn is proportional to system parameters. What this interpretation actually means is that under standard conditions and with improved device precision and sensitivity, experiments should be able to expose as much as possible FQHS.
The intuitive meaning of the infinities ![]()
can be clarified further. Another important interpretation can be made. ![]()
corresponds, up to a factor of some function ![]()
of the filling fraction, the activation energy gap, ![]()
measured in Kelvin, K. To estimate the gap, we write ![]()
and expand ![]()
in the neighborhood of one of the transition points; ![]()
and ![]()
as shown in Figure 4. After applying some simplifying approximations, we obtained![]()
. Where ![]()
is the degeneracy of ![]()
-fraction. For example, with ![]()
and![]()
, we have![]()
. Similarly, one has![]()
, ![]()
, ![]()
, ![]()
,![]()
. These values agreed favorably with results recently announced in [15] [16] .
Generally, important aspects of the anomalous viscosity are the anomalous, ![]()
and thermal Hall, ![]()
terms. Their effects come in two folds. 1) They reconstruct vortex density by introducing non-linearities in the fluid dynamics making flows at different fractionally quantized Hall states distinguishable. 2) ![]()
captures temperature variations due to strain effects through ![]()
as soon as vortices are formed. The combined effect make viscosity more robust over wider temperature range and can even enhanced observation of weaker fractional quantum Hall states. Controlling these parameters can improve observablity of weaker fractions and expose weaker ones. Moreover, knowing these parameters may be critical in strained-engineered devices. Since device sensitivity to stress-preserving deformation depends on the factors.
The anomalous and Hall expansion terms shift ![]()
to higher values. We found ![]()
that has been difficult to measure in experiments or wrongly estimated in theory. We found that our estimated gaps compares favorably with literature results [15] [16] .
4. Conclusions
In conclusion, we have computed dissipationless (anomalous) viscosity of quantum vortex Hall states in graphene within hydrodynamics using quantum many-vortex picture of Euler hydrodynamics. The hydrodynamics formalism allowed a great deal of simplifications as the microscopic theory is completely unnecessary and only few variables, ![]()
and ![]()
are employed.
We constructed a general expression to compute viscosity of a fractional quantum Hall fluid. The temperature dependence is also analyzed. Using a Gaussian temperature profile, we demonstrated strongly that anomalous viscosity can be used as tool to measure strength of fractional fillings of Hall fluid. Relying on this principle, we actually showed that experimental observable fractions correspond to infinities in viscosity at some critical
temperatures. We associate the temperatures to energy gaps within ![]()
Hall states, and employ idea to further estimate the bulk excitation gaps of the states. The critical temperatures are contained within some temperature continuum. We physically interpreted the continuum as a host of many, yet undiscovered Hall states. Away from the infinite viscosity limits, the viscosity curves exhibited flatness, which is an indicative region for dissipationless transport.
Finally, our results could be applied to strained-engineered devices to control viscosity. The studies should be able to guide future experiments towards observing new fractions. In particular, the temperature continuums may be probed, though away from the transition zones, for new fractions by controlling the Hall expansion coefficient parameter. Moreover, our work may clarify issues or resolve conflicts of different reported energy gaps, specifically, the ![]()
gap.
Acknowledgements
M. Rabiu thanks International Center for Theoretical Physics (ICTP) for hospitality and for provision of travel grants to conduct part of this research at its center in Trieste, Italy. M. Rabiu also thanks the Condense Matter Physics (CMP) section of ICTP for indebt discussions.