A Review of Wavelets Solution to Stochastic Heat Equation with Random Inputs ()
Received 6 November 2015; accepted 20 December 2015; published 23 December 2015

1. Introduction
Several applications in science and engineering involve stochasticity in input data. This is usually the result of the stochastic nature of the model coefficients, boundary or initial conditions data, the geometry in which the problem is set, and the source term. Uncertainty may also be introduced into an applied problem owing to the intrinsic variability inherent in the system being modelled [1] . Generally, stochastic volatility leads to randomcoefficients in model equations.
The stochastic heat equation with random inputs (SHERI) is a stochastic partial differential equation (SPDE) that has received considerable attention in recent years. The approach to the solution depends on the type of random input present in the equation. Usually, the SHERI is analyzed and solved for only a random source term or for random coefficients only (see for example [2] ). In this paper, we analyze the wavelet solution to the SHERI where both a random source term and random coefficient are present. The equation is given by:
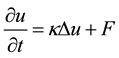 (1)
(1)
In this case, 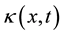 is random coefficient and F is the random source term. In this form, the SHERI usually leads to a complex nonlinear solution.
is random coefficient and F is the random source term. In this form, the SHERI usually leads to a complex nonlinear solution.
Currently, several numerical methods are available for solving SPDEs. These include the classical and popular Monte Carlo method (MCM), the stochastic Galerkin method (SGM), and the stochastic collocation method (SCM). It is well known that MCMs have very slow convergence rates since they do not exploit the regularity available in the solution of SPDE’s with respect to input stochastic parameters. Stochastic Galerkin methods and SCM’s tend to have faster convergence rates compared to MCM’s. However, often, scientific and engineering problems involve irregular dependencies of the quantity of interest with respect to the random variable. As such, SGM’s and SCM’s become inefficient and may not converge at all [3] .
In order to overcome the pitfall of global approximation, localized methods are used to arrest the inefficiencies inherent in SCM’s and SGM’s. Adaptive wavelet collocation methods are relied upon to remedy this situation. The use of this method has the additional advantage of eliminating the dreaded curse of dimensionality. Moreover, it maintains a better convergence rate in addition to producing optimal approximation, not only for PDE's, but also, for PDE-constrained optimal problems [4] . We consider wavelet based-methods in this paper.
Wavelet-based methods for solving differential equations may be classified in two ways, the wavelet collocation methods and the adaptive wavelet schemes. To implement the adaptive wavelet scheme, we consider a second-generation wavelets constructed form the lifting scheme. Wavelets constructed in this form constitute a Riesz basis and have compact support, the desirable properties that guarantee a multiresolution analysis and required approximation.
The rest of the paper is organized as follows: In Section 2 we review the concept of multiresolution analysis in wavelet bases. This is one of the key concepts that will be used in the paper. In addition, the general properties of wavelet solutions to SPDE’s are considered. Section 3 analyzes the solution of the SHE with random coefficients. The stochastic heat equation with random source term is solved in Section 4, while a detail analysis of the full stochastic heat equation with all types of random inputs is solved and analyzed in Section 5. The paper ends with the conclusion in Section 6.
2. Preliminaries
2.1. Wavelets and Multiresolution Analysis
A wavelet is a function  in
in  such that
such that , is an orthonormal basis for
, is an orthonormal basis for . We outline here some of the ideas which are fundamental to the general approach to the theory of wavelets. The concept of multiresolution analysis is central to our discussions. A multiresolution analysis is a decomposition of the Hilbert space
. We outline here some of the ideas which are fundamental to the general approach to the theory of wavelets. The concept of multiresolution analysis is central to our discussions. A multiresolution analysis is a decomposition of the Hilbert space 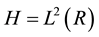 into a chain of closed subspaces
into a chain of closed subspaces 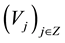 which form a sequence of successive approximation subspaces of H such that the following hold:
which form a sequence of successive approximation subspaces of H such that the following hold:
1) 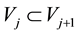 for all
for all 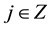
2) 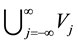 is dense in
is dense in 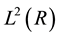 and
and 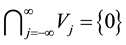
3)  for all
for all 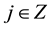
4) ![]() for all
for all ![]()
5) Each subspace Vj is spanned by integer translates of a single function![]() . That is, for any
. That is, for any ![]() and any
and any![]() . All subspaces are therefore scaled versions of the central space V0.
. All subspaces are therefore scaled versions of the central space V0.
6) There exists a function![]() , belonging to V0, such that the sequence
, belonging to V0, such that the sequence ![]() forms a Riesz basis or unconditional basis for V0. The approximation of a function
forms a Riesz basis or unconditional basis for V0. The approximation of a function ![]() at a resolution 2j is defined as the orthogonal projection of
at a resolution 2j is defined as the orthogonal projection of ![]() on Vj. In general a function
on Vj. In general a function ![]() may be approximated by its projection
may be approximated by its projection ![]() onto the space Vj. To compute the orthogonal projection requires that there exists a unique function
onto the space Vj. To compute the orthogonal projection requires that there exists a unique function![]() , which property (6) assures us of. The orthogonal projection of
, which property (6) assures us of. The orthogonal projection of ![]() on Vj is then defined by:
on Vj is then defined by:
![]() (2)
(2)
where
![]() (3)
(3)
2.2. Wavelets
The goal of multiresolution analysis is to develop representations of a function ![]() at various levels of resolution 2j. To achieve this we seek to expand the given function in terms of basis functions
at various levels of resolution 2j. To achieve this we seek to expand the given function in terms of basis functions ![]() which can be scaled to give multiple resolutions of the original function. The notion of scale implies that the function is replaced at a given level (scale) by the best approximation that can be drawn at that scale (subspace). We give two examples of the the most commonly applied wavelets.
which can be scaled to give multiple resolutions of the original function. The notion of scale implies that the function is replaced at a given level (scale) by the best approximation that can be drawn at that scale (subspace). We give two examples of the the most commonly applied wavelets.
First, we define the Haar wavelet. Let X denote an infinite dimensional Banach space. A set ![]() in X
in X
such that![]() , for all n and such that for every
, for all n and such that for every ![]() there is a unique sequence of scalars
there is a unique sequence of scalars![]() , for which
, for which![]() , or
, or ![]() as
as ![]() is called a Schauder basis for X. A Schauder basis
is called a Schauder basis for X. A Schauder basis ![]() for a separable Banach space X is called an absolute basis if whenever
for a separable Banach space X is called an absolute basis if whenever ![]() converges then
converges then ![]() converges for every subsequence of indices ni. The Haar orthogonal system (see for example [7] ) forms an absolute basis for the spaces
converges for every subsequence of indices ni. The Haar orthogonal system (see for example [7] ) forms an absolute basis for the spaces![]() .
.
In the space![]() ,
, ![]() the Haar system of functions
the Haar system of functions ![]()
![]() ;
; ![]() defined by
defined by![]() , for all
, for all![]() ,
,
![]()
![]()
and where we put ![]() equal to the average of the left hand and right hand limits at the finite set of points where it is not defined. Then the Haar system is a Schauder basis for
equal to the average of the left hand and right hand limits at the finite set of points where it is not defined. Then the Haar system is a Schauder basis for![]() ,
,![]() . The Haar system of functions is the precursor and generalization to the Haar wavetets. The Haar wavelets are the given by:
. The Haar system of functions is the precursor and generalization to the Haar wavetets. The Haar wavelets are the given by:
![]() (4)
(4)
![]() (5)
(5)
The Haar basis is convenient for![]() ,
, ![]() , that is, it is an unconditional basis. It is however not suitable for smoother function spaces such as
, that is, it is an unconditional basis. It is however not suitable for smoother function spaces such as ![]() spaces (Sobolev spaces). In this case
spaces (Sobolev spaces). In this case ![]() and
and ![]() have support widths 1, hence this is an example of an orthonormal basis of compactly supported wavelets. However they are not suitable for the study of continuous function spaces since they would not belong to the spaces. A more suitable basis is the Daubechies wavelets.
have support widths 1, hence this is an example of an orthonormal basis of compactly supported wavelets. However they are not suitable for the study of continuous function spaces since they would not belong to the spaces. A more suitable basis is the Daubechies wavelets.
In general Daubechies wavelets depend on an integer ![]() and N even. They arise out of insisting on the requirement that the scaling function
and N even. They arise out of insisting on the requirement that the scaling function ![]() be able to exactly represent polynomials of order up to, but not greater than p, where
be able to exactly represent polynomials of order up to, but not greater than p, where![]() . Daubechies wavelets are defined in terms of their scaling functions. Thus, these (scaling) functions determine the nature of the wavelet function. They are defined as follows:
. Daubechies wavelets are defined in terms of their scaling functions. Thus, these (scaling) functions determine the nature of the wavelet function. They are defined as follows:
For![]() , a Daubechies wavelet of class
, a Daubechies wavelet of class ![]() is a function
is a function ![]() defined by:
defined by:
![]() (6)
(6)
where ![]() are filter coefficients satisfying prescribed conditions. Daubechies wavelets improves the simpler Haar wavelets by making use of longer filters. This results in smoother scaling functions and wavelets. In addition, the larger the size
are filter coefficients satisfying prescribed conditions. Daubechies wavelets improves the simpler Haar wavelets by making use of longer filters. This results in smoother scaling functions and wavelets. In addition, the larger the size ![]() of the filter, the higher is the number k of vanishing moment. A high number of vanishing moments leads to a better compression of regular parts of the function. However, increasing the number of vanishing moments also inceases the size of the support of the wavelets, leading to problems in analysis at discontinuous points in a function.
of the filter, the higher is the number k of vanishing moment. A high number of vanishing moments leads to a better compression of regular parts of the function. However, increasing the number of vanishing moments also inceases the size of the support of the wavelets, leading to problems in analysis at discontinuous points in a function.
2.3. Weak and Strong Solutions of SDE
Solutions of SDE’s may be classified as weak or strong. If there exist a probability space with filtration, Brownian motion ![]() adapted to that filtration, a process
adapted to that filtration, a process ![]() adapted to that filtration, such that
adapted to that filtration, such that ![]() has distribution
has distribution![]() , and for all t integrals below are defined, and
, and for all t integrals below are defined, and ![]() satisfies:
satisfies:
![]() (7)
(7)
then ![]() is called the weak solution to the SDE
is called the weak solution to the SDE
![]() (8)
(8)
A weak solution of the stochastic differential equation above is a triple![]() ,
, ![]() ,
, ![]() where
where ![]() is a probability space equipped with the filtration
is a probability space equipped with the filtration ![]() that satisfies the usual conditions; X is a continuous,
that satisfies the usual conditions; X is a continuous, ![]() -adapted
-adapted ![]() -valued process and W is ans m-dimensional
-valued process and W is ans m-dimensional ![]() -Brownian motion on the space; and the conditions:
-Brownian motion on the space; and the conditions:
![]() (9)
(9)
holds for all![]() . Hence we have:
. Hence we have:
![]() (10)
(10)
![]() is called a strong solution to the equation above with initial value
is called a strong solution to the equation above with initial value ![]() if for all t > 0,
if for all t > 0, ![]() is a func- tion
is a func- tion ![]() of the given brownian motion
of the given brownian motion ![]() and
and![]() , integrals
, integrals ![]() and
and ![]() and the integral equation below is satisfied.
and the integral equation below is satisfied.
![]() (11)
(11)
2.4. Wavelet Approximation to Stochastic Differential Equations
The solution of a SDE requires the evaluation of an integral of the type:
![]()
where ![]() may be considered as a fractional Brownian motion (FBM) and S is a stochastic process. To accomplish this, the above stochastic integral must be approximated by representing it with respect to FBM using fractional integrals. This approximation can be used for SDE’s without explicit solution, if the equation is driven by fractional noise. Optimal wavelet approximations may be used to develop efficient simulations. The method may be summarized as follows:
may be considered as a fractional Brownian motion (FBM) and S is a stochastic process. To accomplish this, the above stochastic integral must be approximated by representing it with respect to FBM using fractional integrals. This approximation can be used for SDE’s without explicit solution, if the equation is driven by fractional noise. Optimal wavelet approximations may be used to develop efficient simulations. The method may be summarized as follows:
1) Obtain an approximation for fractional noise
2) Apply an appropriate numerical scheme (for example, implicit or explicit Euler scheme) to obtain an approximation of the solution
3) Prove the almost sure convergence of the approximation to the solution.
Let ![]() denote the one dimensional FBM with hurst index
denote the one dimensional FBM with hurst index ![]() (Gaussian random process).
(Gaussian random process).
If![]() , the classical stochastic integration is not applicable. However, by the Holder continuity of B,
, the classical stochastic integration is not applicable. However, by the Holder continuity of B,
![]() , defined in terms of fractional integration exists. The optimal wavelet approximation of the FBM
, defined in terms of fractional integration exists. The optimal wavelet approximation of the FBM ![]() with Hurst index H is given by
with Hurst index H is given by
![]() (12)
(12)
where ![]() is the mother wavelet and
is the mother wavelet and ![]() are i.i.d
are i.i.d ![]() random variables.
random variables.
The fractional integral of the function f with respect to the function g is defined as:
![]() (13)
(13)
If![]() ,
, ![]() for
for![]() . Let
. Let![]() . We consider the fractional integral over
. We consider the fractional integral over![]() . Then
. Then
![]() (14)
(14)
where ![]() and
and
![]() (15)
(15)
![]() (16)
(16)
See, for example, [6] .
2.5. Second Generation Wavelets
Second-generation wavelets are a generalized form of bi-orthogonal wavelets. Their applications easily fit functions defined on bounded domains. These wavelets form a Riesz basis for certain desirable function spaces. The lifting scheme is a method for constructing second generation wavelets that are no longer translates and dilates of a single scaling function. The lifting scheme is given by:
![]() (17)
(17)
See, for example, [1] .
2.6. The Wavelet Stochastic Collocation Method
The second generation collocation method makes the treatment of nonlinear terms in PDE’s easier to handle. Moreover, the use of wavelets enables the solution of differential equations with localized structures or sharp transitions more amenable. In order to solve such problem more efficiently, the use of computational grids that adapts dynamically in time to reflect local changes in the solution play an effective role.
Wavelet-based numerical algorithms may be classified into two main types namely the wavelet-Garlekin method and the wavelet collocation method. The wavelet-Garlekin algorithm uses gridless wavelet coefficient space while the collocation method relies on dynamically adaptive computational grid [8] . A clear advantage of the wavelet-collocation method is that it facilitates the easy treatment of nonlinear terms in a stochastic partial differential equation. However, traditional biorthogonal wavelets are not suitable for handling boundaries. Omitting the translation-dilation relationship, biorthogonal wavelets, leads to second generation wavelets [9] which uses second generation MRA of a function space as given below.
Let ![]() where L is the function space.
where L is the function space.
1) ![]()
2) ![]() is dense in L, and
is dense in L, and
3) for each![]() ,
, ![]() contains a Reisz basis given by the scaling function
contains a Reisz basis given by the scaling function![]() , where
, where ![]() denotes some index set.
denotes some index set.
Since![]() , it follows that
, it follows that![]() . Hence
. Hence
![]() (18)
(18)
Here, the MRA is not based on the scaling function![]() . It is rather defined in terms of the filter coefficients
. It is rather defined in terms of the filter coefficients ![]() that satisfies (16). The resulting wavelets become the basis functions for
that satisfies (16). The resulting wavelets become the basis functions for![]() , the complement of
, the complement of ![]() in
in![]() . It follows that
. It follows that![]() . Hence the second generation wavelets form a Reisz basis for the funtional space L. It follows that wavelets at level j can be expressed in terms of the scaling functions as follows:
. Hence the second generation wavelets form a Reisz basis for the funtional space L. It follows that wavelets at level j can be expressed in terms of the scaling functions as follows:
![]() (19)
(19)
Since![]() , it follows that
, it follows that
![]() (20)
(20)
Given the scaling function coefficients![]() , we have:
, we have:
![]() (21)
(21)
where ![]() and
and![]() .
.
Second generation wavelet transform may be considered in terms of filter banks, where filters not only act locally but may be potentially different for each coefficient. Now we can set
![]() (22)
(22)
where![]() . The interpolating function has the following properties:
. The interpolating function has the following properties:
1) Compact support that is zero outside the interval![]() .
.
2) ![]() is interpolating, that is
is interpolating, that is![]() .
.
3) Linear combinations of ![]() reproduce the polns up to degree
reproduce the polns up to degree ![]()
4) ![]() satisfies the refinement relation
satisfies the refinement relation
![]() (23)
(23)
5) ![]() is the autocorrelation of Daubechies scaling functions of order 2N.
is the autocorrelation of Daubechies scaling functions of order 2N.
Define the detail function as:
![]() (24)
(24)
Hence![]() .
.
The lifting scheme is applied to infinite or periodic domains for the construction of the first-generation wavelets. The lifting scheme has the following advantages:
1) Faster implementation of the wavelet transform by a factor of 2.
2) No auxiliary memory required. The original signal is replaced with its wavelet transform.
3) Inverse wavelet transform is simply the reversal of the order of operations and switching of addition and operations. The scaling function and mother wavelet have vanishing moments, that is
![]() (25)
(25)
![]() (26)
(26)
where D is the domain over which the wavelets are constructed.
2.7. Grid Adaptation
Consider the function ![]() defined on a closed interval
defined on a closed interval![]() . Consider the grid
. Consider the grid
![]() (27)
(27)
where the grid points ![]() may be uniformly or nonuniformly placed. For nested grids,
may be uniformly or nonuniformly placed. For nested grids, ![]() we must have
we must have![]() . From the secon generation wavelets we have:
. From the secon generation wavelets we have:
![]() (28)
(28)
[8] . Let ε denote the prescribed threshold, then the approximation ![]() may expressed as the sum of two terms made up of wavelets whose amplitude is above and below the threshold. That is:
may expressed as the sum of two terms made up of wavelets whose amplitude is above and below the threshold. That is:
![]() (29)
(29)
where
![]() (30)
(30)
![]() (31)
(31)
Hence
![]() (32)
(32)
and the number of significant wavelet coefficients ![]() is bounded by ε as
is bounded by ε as
![]() (33)
(33)
where the coefficients ![]() depend on
depend on![]() . Thus
. Thus
![]() (34)
(34)
The adaptive grid is calculated as follows:
1) Sample ![]() on the grid
on the grid ![]()
2) Perform the forward wavelet transform to obtain the values of ![]() and
and![]() .
.
3) Analyze wavelet coefficients ![]() and create a mask M for the grid points
and create a mask M for the grid points![]() , associated with wavelets for which
, associated with wavelets for which![]() .
.
4) Incorporate into the mask M all grid points associated with the scaling functions at the coarsest level of res- olution.
5) Starting from ![]() level of resolution, recursively extend the mask to include grid points of the coarser level of resolution necessary for computing wavelet coefficients at level j hat are masked by the mask M.
level of resolution, recursively extend the mask to include grid points of the coarser level of resolution necessary for computing wavelet coefficients at level j hat are masked by the mask M.
The process of grid adaptation for the solution of PDE’s is made up of the following steps [10] :
1) Use the values of the solution ![]() at
at ![]() computational grid to compute the values of wavelet coefficients corresponding to each component of the solution using forward wavelet transform.
computational grid to compute the values of wavelet coefficients corresponding to each component of the solution using forward wavelet transform.
2) Analyze wavelet coefficients ![]() and creat a mask M for the grid points
and creat a mask M for the grid points![]() , associated with wavelets for which
, associated with wavelets for which![]() .
.
3) Extend the mask M with grid points associated with type I or II adjacent wavelets.
4) Perform the reconstruction check procedure to obtain a complete mask M.
5) Construct the new computational grid![]() , which will be used for the next step of time integration.
, which will be used for the next step of time integration.
When solutions of differential equations are intermittent in both space and time, methods combining adjustable time step with spatial grid to obtain approximate solutions. However, several problems depend on small spatial scales that are highly localized and as such, using a uniformly fine grid does not necessarily lead to and efficient method of solution. To address this concern, locally adapted grids are appealed to.
Wavelets can be used to used as an efficient tool to develop adaptive numerical methods capable of limiting the global approximation error associated with the numerical scheme. In addition to being fast, such wavelet- based schemes are asymptotically optimal when applied to elliptic differential equations [10] [11] . Moreover, they are fast.
The second generation adaptive wavelet can be used to discretize PDE’s as follows:
![]() (35)
(35)
![]() (36)
(36)
where ![]() is a general partial differential operator,
is a general partial differential operator, ![]() an operator that defines applicable boundary conditions, and
an operator that defines applicable boundary conditions, and![]() , where
, where![]() ,
,![]() . Here, Ω is an open, connected, and bounded set with boun- dary
. Here, Ω is an open, connected, and bounded set with boun- dary![]() . We denote a point in Ω by
. We denote a point in Ω by![]() . Consider the multiscale decomposition
. Consider the multiscale decomposition
![]() (37)
(37)
where ![]() is a localized basis function and
is a localized basis function and ![]() are the expansion coefficients. The truncated sum
are the expansion coefficients. The truncated sum ![]() is a good approximation of
is a good approximation of ![]() at level J. it follows that
at level J. it follows that
![]() (38)
(38)
In order to construct grid points that adapt to intermittent solution, we consider the collocation points ![]() such that
such that![]() . That is:
. That is:
![]() (39)
(39)
The second generation wavelet decomposition takes the form:
![]() (40)
(40)
[9] This approximation is known as nonlinear approximation in wavelet basis. The method is a combination of the fast second generation wavelet transform with finite difference approximation of derivatives.
3. The Case of Random Input Coefficient
In real thermal environments, the heat transfer coefficient of media surfaces are subject to temporal and spatial variations due to several factors [12] . However, accurately predicting spatial distribution of the heat transfer coefficient is very complicated since these external influences are usually nonlinear and are fleeting in nature [13] . In addition, the complexity is compounded by a measurement uncertainty of more than fifty percent for the overall heat transfer coefficients of heat transfer surfaces during heat exchangers [14] . Due to the inherent uncertainties described above, the distribution of temperature and thermal stresses in media is analyzed taking into account probability theory. The stochastic heat equation devoid of a source term but characterized by a random input is given by
![]() (41)
(41)
with![]() . The solution depends on the nature of the random coefficient, κ. If κ is a constant, the above equation simply becomes the standard heat equation with the solution given by:
. The solution depends on the nature of the random coefficient, κ. If κ is a constant, the above equation simply becomes the standard heat equation with the solution given by:
![]() (42)
(42)
If κ is random, three possible approaches to the solution are possible. Two of these methods are provided by [15] . We outline the third method here. We assume that the stochastic input coefficient κ satisfies ![]() is positive and uniformly bounded almost surely, that is:
is positive and uniformly bounded almost surely, that is:
![]() (43)
(43)
In this case the solution is a complex nonlinear function of the coefficient κ [16] . A reasonably approximate solution may be obtained by applying the stochastic collocation method or the adaptive wavelet stochastic method [1] . This method exploits the properties of compactly supported wavelet that form Reisz bases. When implemented as interpolating wavelet bases, they induce norms that are ![]() -stable, and they constitute a stable multiresolution analysis of the stochastic space
-stable, and they constitute a stable multiresolution analysis of the stochastic space![]() . In addition the composition of the wavelet basis eliminates the difficulty associated with solutions made up of dense stiff matrices. The number of wavelet coefficients at each resolution 2J is approximately constant [17] .
. In addition the composition of the wavelet basis eliminates the difficulty associated with solutions made up of dense stiff matrices. The number of wavelet coefficients at each resolution 2J is approximately constant [17] .
We assume a stochastic solution of the form:
![]() (44)
(44)
where W0 = 1 and ![]() is the mean solution and
is the mean solution and ![]() is the wavelet basis [18] . where 0 < κmin < κmax < ∞. Here,
is the wavelet basis [18] . where 0 < κmin < κmax < ∞. Here, ![]() is a wavelet Riesz basis for
is a wavelet Riesz basis for ![]() where J denotes the scale parameter. The expansion represents a stochastic process in the form of a linear combination of orthonormal wavelet basis. We assume that the stochastic source is controlled by an independent Wiener process on a complete probability space
where J denotes the scale parameter. The expansion represents a stochastic process in the form of a linear combination of orthonormal wavelet basis. We assume that the stochastic source is controlled by an independent Wiener process on a complete probability space ![]() [19] .
[19] .
To obtain the approximation given by the equation above which yields an optimal wavelet basis by minimizing the total mean square error, we consider the sample space Ω equipped with the ![]() -algebra
-algebra ![]() and the probability measure
and the probability measure![]() . Together they form the probability space
. Together they form the probability space![]() . Let
. Let
![]() (45)
(45)
where ![]() denotes the mean of
denotes the mean of![]() , and where
, and where ![]() are eigenpairs of the covariance kernel
are eigenpairs of the covariance kernel![]() . That is, for
. That is, for
![]() (46)
(46)
and
![]() (47)
(47)
and the random variables ![]() are defined by:
are defined by:
![]() (48)
(48)
where ![]() are of zero mean and uncorrelated.
are of zero mean and uncorrelated.
4. Stochastic Heat Equation with Source Term
We consider the heat equation with an additional forcing term. The quation now becomes:
![]() (49)
(49)
A weak solution may be given as
![]() (50)
(50)
where ![]() is a smooth kernel. While this solution is valid for several distributions F, it is not valid for all. We consider the case where F is a space-time white noise. For any fixed location in space, the solution to the SHE
is a smooth kernel. While this solution is valid for several distributions F, it is not valid for all. We consider the case where F is a space-time white noise. For any fixed location in space, the solution to the SHE
which is almost Holder-![]() . However the solution has temporal regularity resembling Brownian Motion (BM).
. However the solution has temporal regularity resembling Brownian Motion (BM).
The greatest difficulty encountered in solving this problem involves the representation of the source term. [20] [21] have shown that spectral methods can be relied upon to obtain an accurate enough solution. Thus, we assume a solution of the form:
![]() (51)
(51)
where uk are deterministic coefficients and![]() ,
, ![]() are orthogonal wavelet basis, instead of multidimensional Hermite polynomials [22] . Similar to the Karhunen-Loève expansion, this method generates optimal basis. This means that truncating the first L levels of wavelet resolution yields enough accuracy. The approximation of the function
are orthogonal wavelet basis, instead of multidimensional Hermite polynomials [22] . Similar to the Karhunen-Loève expansion, this method generates optimal basis. This means that truncating the first L levels of wavelet resolution yields enough accuracy. The approximation of the function ![]() can be represented as:
can be represented as:
![]() (52)
(52)
For any intermediate resolution level j (0 ≤ j < J) we have
![]() (53)
(53)
where ![]() and apply the wavelet collocation method (see for example [5] ).
and apply the wavelet collocation method (see for example [5] ).
Ususlly, ![]() where G is the fundamental solution to the problem
where G is the fundamental solution to the problem ![]() .
.
5. SHERI
We consider the partial differential equation with random inputs in the form:
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
where ![]() denotes the gradient operator with respect to
denotes the gradient operator with respect to![]() , with the assumption that
, with the assumption that ![]() , with
, with![]() . For finite dimensional noise, the stochastic coefficient
. For finite dimensional noise, the stochastic coefficient ![]() satisfies the condition above and
satisfies the condition above and ![]() satisfies:
satisfies:
![]() (57)
(57)
where![]() . In addition, the stochastic input data have the form:
. In addition, the stochastic input data have the form:
![]() (58)
(58)
where ![]() and
and ![]() is a real-valued vector of independent random variables [1] [23] .
is a real-valued vector of independent random variables [1] [23] .
Using polynomials that have the property of diagonal interpolation matrix, leads to the stochastic collocation method. We re-formulate the problem by letting D denote a bounded domain in![]() ,
, ![]() and Ω,
and Ω, ![]() , P denote a complete probability space, where Ω denotes the sample space and
, P denote a complete probability space, where Ω denotes the sample space and![]() , the
, the ![]() -algebra of events and
-algebra of events and ![]() is a probability measure. The representation of a general second-order random process by generalized polynomial [24] . This leads us to consider the stochastic initial boundary value problem:
is a probability measure. The representation of a general second-order random process by generalized polynomial [24] . This leads us to consider the stochastic initial boundary value problem:
Theorem 1. Find ![]() such that P-almost surely in Ω.
such that P-almost surely in Ω.
![]() (59)
(59)
where ![]() denotes the differential operator and
denotes the differential operator and ![]() denotes a boundary operator.
denotes a boundary operator.
The above problem may be solved using Lagrange Interpolation in parameter space. Let ![]() denote a set of distinct points in parameter space, and let
denote a set of distinct points in parameter space, and let ![]() denote a set of basis functions. We seek the approximation
denote a set of basis functions. We seek the approximation ![]() of the solution u of the problem above, of the form:
of the solution u of the problem above, of the form:
![]() (60)
(60)
After solving for the finite element approximation of the solution![]() , we solve for the finite element approximation of each interpolation point in the set
, we solve for the finite element approximation of each interpolation point in the set![]() . The coefficients
. The coefficients ![]() are then determined by imposing the condition:
are then determined by imposing the condition:
![]() (61)
(61)
Instead of using global polynomial interpolating spaces, piecewise polynomial interpolation spaces requiring only a fixed polynomial degree is needed. this method is based on refining the grid used and is suitable for problems having solutions with irregular behavior.
For each parameter dimension![]() , define
, define![]() . The required approximation is based on a sequence of subspaces
. The required approximation is based on a sequence of subspaces ![]() of V of increasing dimension
of V of increasing dimension ![]() which is dense in
which is dense in![]() , that is,
, that is,![]() . The sequence of spaces must be nested in the wavelet multiresolution analysis of the form:
. The sequence of spaces must be nested in the wavelet multiresolution analysis of the form:
![]()
where
![]()
and where ![]() represents the scaling level of all the basis functions
represents the scaling level of all the basis functions ![]() with compact support (that is,
with compact support (that is, ![]() , and
, and ![]() is a polynomial of degree p). For n N-dimensional problem, define
is a polynomial of degree p). For n N-dimensional problem, define![]() . Then the sequence of subspaces
. Then the sequence of subspaces ![]() of
of ![]() is given by
is given by
![]() (62)
(62)
where ![]() is a multi-index and
is a multi-index and![]() . The finer subspaces
. The finer subspaces ![]() are defined as the direct sum
are defined as the direct sum
![]() (63)
(63)
hence we have:
![]() (64)
(64)
The hierarchical sparse-grid approximation of L is given by:
![]() (65)
(65)
where ![]() and
and ![]() denotes the approximation operator,
denotes the approximation operator,
![]() denotes a multi-dimensional hierachical polynomial. The
denotes a multi-dimensional hierachical polynomial. The ![]() multi-index is defined by:
multi-index is defined by:
![]()
The approximation spaces ![]() and the chosen basis have the following properties:
and the chosen basis have the following properties:
1) ![]()
2) Supp ![]()
3) ![]() is an interpolating basis for
is an interpolating basis for ![]()
4) There is a constant C, independent of the level L, such that
![]()
For example, consider the hat function:
![]()
The major disadvantage of this that the linear hierarchical basis does not form a stable multiscale splitting of the approximation scale. The scheme does not ensure efficiency and optimality with respect to complexity as previously claimed.
A multi-resolution wavelet approximation though similar, performs better to achieve optimality since it possesses the additional property:
5) Riesz Property: The basis ![]() is a Riesz basis. Hence there exists a constant
is a Riesz basis. Hence there exists a constant![]() , independent of the level L for all
, independent of the level L for all![]() , the following is true
, the following is true
![]() (66)
(66)
By implication, other methods without this property are not ![]() stable.
stable.
6. Conclusion
Analytical Error Estimates
Suppose the wavelet decomposition is truncated at level J, we define the residual of the truncation by
![]() (67)
(67)
This error is a function of the wavelet thresholding parameter ![]() and the order of the wavelets. If
and the order of the wavelets. If ![]() is a sufficiently smooth function, there exits
is a sufficiently smooth function, there exits ![]() such that
such that![]() ,
,![]() . Hence the residual approximation at level J is bounded above [25] - [27] , and
. Hence the residual approximation at level J is bounded above [25] - [27] , and
![]() (68)
(68)
![]() (69)
(69)
Wavelets can handle periodic boundary conditions efficiently. Moreover, the use of antiderivatives of wavelet bases as trial functions smoothen singurarities in wavelets. The basic principle is summarized as follows:
1) Represent the geometric region for the bvp in terms of wavelet series.
2) Represent the functions defined on the boundary and on the interior of the region in terms of wavelet series defined on a rectangular region containing the domain.
3) Convert the differential equation to some weak form.
4) Formulate and solve the wavelet Garlerkin problem for the domain and differential equation, using localized wavelets as orthonormal basis.
An important property of this method is that the coding for the solution is independent of the geometry of the boundary [28] . The wavelet basis is more efficient than finite element basis for the approximation of the boundary measure. The associated error E is given by:
![]() (70)
(70)
We have shown that wavelet-based solution to the stochastic heat equation with random inputs is stable. Computational methods based on the wavelet transform are analyzed for every possible type of stochastic heat equation. The methods are shown to be very convenient for solving such problems, since the initial and boundary conditions are taken into account automatically. The results reveal that the wavelet algorithms are very accurate and efficient.
NOTES
![]()
*Corresponding author.