Numerical Study for Simulation the MHD Flow and Heat-Transfer Due to a Stretching Sheet on Variable Thickness and Thermal Conductivity with Thermal Radiation ()
1. Introduction
The previous investigations ([1] -[6] ) did not study the effects of radiation on the flow and heat transfer. In manufacturing industries, the radiative heat transfer flow is very important for the design of reliable equipments, nuclear plants, gas turbines and various propulsion devices for aircraft, missiles, satellites and space vehicles. Also, the effect of thermal radiation on the forced and free convection flows is important in the context of space technology and processes involving high temperature. Historically in ([7] - [10] ), the study on boundary layer flows over a stretching sheet with variable thickness is presented. From these considerations, we can see that the effects of the non-flatness on the stretching sheet problems considering a variable sheet thickness have not presented. So, the main goal of this paper is to introduce the numerical simulation using Chebyshev spectral method ([11] -[16] ) for the proposed model.
2. Formulation of the Model
In this section, we will consider a steady, 2Dim boundary layer flow of an incompressible Newtonian fluid over a continuously impermeable stretching sheet. The origin is located at a slit, through which the sheet is drawn through the fluid medium (see Figure 1). The velocity of the stretching surface is given by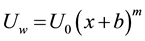 ,
,
where 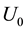 is the reference velocity. We suppose that the sheet is not flat and defined as
is the reference velocity. We suppose that the sheet is not flat and defined as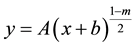 ,
,
where A is a very small constant so that the sheet is sufficiently thin and m is the velocity power index. We must note that the proposed model is satisfied only for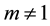 , because for
, because for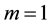 , the model changes to a flat sheet. Likewise, the fluid properties are assumed to be constant except for thermal conductivity variations in the temperature. In this work, we will suppose that the variable magnetic field
, the model changes to a flat sheet. Likewise, the fluid properties are assumed to be constant except for thermal conductivity variations in the temperature. In this work, we will suppose that the variable magnetic field 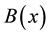 is applied normal to the sheet and that the induced magnetic field is neglected, which is justified for MHD flow at small magnetic Reynolds number.
is applied normal to the sheet and that the induced magnetic field is neglected, which is justified for MHD flow at small magnetic Reynolds number.
In case of approximations for the usual boundary layer of the Newtonian fluid, we can write, the steady 2D im boundary-layer equations taking into account the thermal radiation effect in the energy equation in the following form:
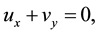 (1)
(1)
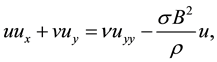 (2)
(2)
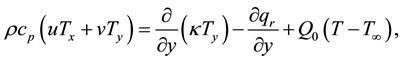 (3)
(3)
![]()
Figure 1. Illustration of a stretching sheet with variable sheet thickness.
where u and v are the velocity components in the x and y directions, respectively. 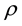 and
and 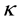 are the fluid density and the thermal conductivity, respectively. T is the temperature of the fluid,
are the fluid density and the thermal conductivity, respectively. T is the temperature of the fluid, 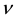 is the fluid kinematic viscosity, B is the strength of the applied magnetic field,
is the fluid kinematic viscosity, B is the strength of the applied magnetic field, 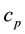 is the specific heat at constant pressure,
is the specific heat at constant pressure, 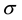 is the electrical conductivity of the fluid,
is the electrical conductivity of the fluid, ![]() is the heat generation/absorption coefficient and
is the heat generation/absorption coefficient and ![]() is the radiative heat flux.
is the radiative heat flux.
The radiative heat flux ![]() is employed according to Rosseland approximation [17] such that
is employed according to Rosseland approximation [17] such that
![]() (4)
(4)
where ![]() is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and ![]() is the mean absorption coefficient. Following Raptis [18] , we assume that the temperature differences within the flow are sufficiently small such that
is the mean absorption coefficient. Following Raptis [18] , we assume that the temperature differences within the flow are sufficiently small such that ![]() may be expressed as a linear function of the temperature. Expanding
may be expressed as a linear function of the temperature. Expanding ![]() in a Taylor series about
in a Taylor series about ![]() and neglecting higher-order terms, we have
and neglecting higher-order terms, we have
![]() (5)
(5)
The physical and mathematical advantage of the Rosseland formula (4) consists of the fact that it can be combined with Fourier’s second law of conduction to an effective conduction-radiation flux ![]() in the form
in the form
![]() (6)
(6)
where ![]() is the effective thermal conductivity. So, the steady energy balance equation include-
is the effective thermal conductivity. So, the steady energy balance equation include-
ing the net contribution of the radiation emitted from the hot wall and absorbed in the colder fluid, takes the form
![]() (7)
(7)
To obtain similarity solutions, it is assumed that the magnetic field ![]() is of the form
is of the form
![]() (8)
(8)
where ![]() is the constant magnetic field. The boundary conditions can be written as
is the constant magnetic field. The boundary conditions can be written as
![]() (9)
(9)
![]() (10)
(10)
The mathematical analysis of the problem is simplified by introducing the following dimensionless coor- dinates
![]() (11)
(11)
where ![]() is the similarity variable,
is the similarity variable, ![]() is the stream function which is defined in the classical form as
is the stream function which is defined in the classical form as ![]() and
and ![]() and
and ![]() is the dimensionless temperature.
is the dimensionless temperature.
In this study, the equation for the dimensionless thermal conductivity ![]() is generalized for the temperature dependence as follows ([19] [20] ):
is generalized for the temperature dependence as follows ([19] [20] ):
![]() (12)
(12)
where ![]() is the ambient thermal conductivity and
is the ambient thermal conductivity and ![]() is the thermal conductivity parameter.
is the thermal conductivity parameter.
Upon using these variables, the boundary layer governing Equations (1)-(3) can be written in a non-dimensional as follows
![]() (13)
(13)
![]() (14)
(14)
where ![]() is the magnetic parameter,
is the magnetic parameter, ![]() is the Prandtl number,
is the Prandtl number, ![]() is the radiation parameter and
is the radiation parameter and ![]() is the heat generation parameter (>0) or the absorption parameter (<0).
is the heat generation parameter (>0) or the absorption parameter (<0).
Also, the boundary conditions transformed to the following form
![]() (15)
(15)
![]() (16)
(16)
where ![]() is a parameter related to the thickness of the wall and
is a parameter related to the thickness of the wall and ![]() indi-
indi-
cates the plate surface. We can write the Equations (13)-(14) in a simple form and to facilitate the computation, if we take into the account the transformation ![]() and
and![]() . So, the similarity equation and the associated boundary conditions become
. So, the similarity equation and the associated boundary conditions become
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
The physical quantities of primary interest are the local skin-friction coefficient ![]() and the local Nusselt number
and the local Nusselt number ![]() which are defined as
which are defined as
![]() (21)
(21)
where ![]() is the local Reynolds number and
is the local Reynolds number and![]() .
.
3. Application of Chebyshev Spectral Method
In this section, we implement Chebyshev spectral method to solve the resulting system of non-linear ODEs of the form (17)-(18) with boundary conditions (19)-(20). To achieve this aim, and since the Gauss-Lobatto nodes
inside![]() , we will use the transformation
, we will use the transformation ![]() to change Equations (17)-(18) to take the following
to change Equations (17)-(18) to take the following
form
![]() (22)
(22)
![]() (23)
(23)
also the boundary conditions will transform to the following form
![]() (24)
(24)
where ![]() and
and ![]() are unknown functions from
are unknown functions from![]() . Where the derivative in (22)-(23) will be w.r.t. the new variable x. The proposed technique is accomplished by starting with a Chebyshev approximation for the highest order derivatives,
. Where the derivative in (22)-(23) will be w.r.t. the new variable x. The proposed technique is accomplished by starting with a Chebyshev approximation for the highest order derivatives, ![]() and
and ![]() and generating approximations to the lower order derivatives
and generating approximations to the lower order derivatives ![]() and
and ![]() as follows: Setting
as follows: Setting ![]() and
and![]() , then by integration we obtain
, then by integration we obtain![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() as follows:
as follows:
![]() (25)
(25)
![]() (26)
(26)
Also using the boundary conditions (24), the constants of integration![]() , can be written as follows
, can be written as follows
![]()
![]()
Now, the approximations to the Equations (25) and (26) will take the following forms
![]() (27)
(27)
where ![]() and
and ![]() are the elements of the matrix B which is defined in [21] .
are the elements of the matrix B which is defined in [21] .
And with implementation the transformation (27), we can write the system (22)-(23) to a form of system of non- linear equations in the highest derivative as follows:
![]() (28)
(28)
![]() (29)
(29)
These equations are non-linear system of 2n + 2 algebraic equations in 2n + 2 unknowns ![]() and
and![]() . After solving this system using Newton’s iteration method and substitution
. After solving this system using Newton’s iteration method and substitution ![]() and
and ![]() in Equation (27), we can obtain the numerical solution of the system of Equations (17)-(18).
in Equation (27), we can obtain the numerical solution of the system of Equations (17)-(18).
4. Results and Discussion
In Table 1 and Table 2, we presented the numerical solution using the Chebyshev spectral method with![]() . These results show excellent agreement with the existing solutions in the literature [10] and show that the proposed method suits for MHD boundary layer flow problems. Also, in this section we provided the behavior of parameters involved in the expressions of heat transfer characteristics for the stretching sheet. The numerical solutions of this problem are performed and illustrated graphically in Figures 2-11. Effects of the magnetic parameter M on velocity and temperature profiles are shown in Figure 2 and Figure 3, respectively. It is observed that the velocity decreases for increasing values of M. Furthermore, the momentum boundary layer thickness decreases as M increases. This is due to the fact that as M increases, the boundary layer flow acquires more magnetization that leads to the variation in Lorentz force which opposes the flow. From Figure 3, we can see that the fluid temperature increases when the magnetic number is increase, because Lorentz force which produces from the presence of transverse magnetic field. When this force increases, the fluid exhibits a resistance to this force by increasing the friction between its layers. The increasing in the temperature caused by this resistance.
. These results show excellent agreement with the existing solutions in the literature [10] and show that the proposed method suits for MHD boundary layer flow problems. Also, in this section we provided the behavior of parameters involved in the expressions of heat transfer characteristics for the stretching sheet. The numerical solutions of this problem are performed and illustrated graphically in Figures 2-11. Effects of the magnetic parameter M on velocity and temperature profiles are shown in Figure 2 and Figure 3, respectively. It is observed that the velocity decreases for increasing values of M. Furthermore, the momentum boundary layer thickness decreases as M increases. This is due to the fact that as M increases, the boundary layer flow acquires more magnetization that leads to the variation in Lorentz force which opposes the flow. From Figure 3, we can see that the fluid temperature increases when the magnetic number is increase, because Lorentz force which produces from the presence of transverse magnetic field. When this force increases, the fluid exhibits a resistance to this force by increasing the friction between its layers. The increasing in the temperature caused by this resistance.
In Figure 4, Figure 5, we presented the obtained numerical results to show the effects of wall thickness parameter on the fluid flow and the temperature distribution. From Figure 4, we can see that the velocity at any point near to the plate decreases as the wall thickness parameter increases. Also from these figures, we can note that the thickness of the boundary layer becomes thinner for a higher value of ![]() and becomes thicker for a smaller value of
and becomes thicker for a smaller value of![]() .
.
Figure 5 displays that the wall thickness parameter decreased the thickness of the thermal boundary layer and enhanced the rate of heat transfer. Physically, increasing the value of ![]() will decrease the flow velocity because under the variable wall thickness, not all the pulling force of the stretching sheet can be transmitted to the fluid causing a decrease for both friction between the fluid layers and temperature distribution for the fluid. Likewise, for a higher value of
will decrease the flow velocity because under the variable wall thickness, not all the pulling force of the stretching sheet can be transmitted to the fluid causing a decrease for both friction between the fluid layers and temperature distribution for the fluid. Likewise, for a higher value of![]() , the thermal boundary layer becomes thinner compared with the smaller value of the same parameter.
, the thermal boundary layer becomes thinner compared with the smaller value of the same parameter.
![]()
Figure 2. The velocity distribution for different values of M.
![]()
Figure 3. The temperature distribution for different values of M.
![]()
Figure 4. The velocity distribution for different values of![]() .
.
From Figure 6, we can ensure that the velocity increases with a decrease in the values of the velocity power index m along the sheet and the reverse is true away from it. This implies that the momentum boundary thickness becomes thicker as m increases.
The influence of the velocity power index parameter m on the temperature profiles is displayed in Figure 7. From this figure, we can see that increasing the value of m produces an increase in the temperature profiles. It further shows that the larger the value of m, the higher the magnitude of the thermal boundary thickness will be.
From Figure 8, we can reveal that the temperature profile as well as the thickness of the thermal boundary layer increase when ![]() increases. Where in this figure, we have changed the thermal conductivity parameter
increases. Where in this figure, we have changed the thermal conductivity parameter ![]() with fixed the values of all other parameters.
with fixed the values of all other parameters.
In Figure 9, we presented the effects of R on the temperature profiles with fixed the values of all other parameters. From this figure, we noted that the temperature field and the thermal boundary layer thickness increase with the increase in R. Also, from Figure 10, we can observe that an increase in the Prandtl number results in decreases the heat transfer profiles. The reason is that increasing values of Prandtl number equivalent for decreasing the thermal conductivities and therefore heat is able to diffuse away from the heated sheet more rapidly. Hence in the case of increasing Prandtl number, the boundary layer is thinner and the heat transfer is reduced.
Figure 11 illustrates the affect on the profiles of temperature distribution with different values of the parameter ![]() where we fixed all values of the other parameters. This figure indicates that the temperature distribution
where we fixed all values of the other parameters. This figure indicates that the temperature distribution
![]()
Figure 5. The temperature distribution for different values of![]() .
.
![]()
Figure 6. The velocity distribution for different values of m.
![]()
Figure 7. The temperature distribution for different values of m.
![]()
Figure 8. The temperature distribution for different values of![]() .
.
![]()
Figure 9. The temperature distribution for different values of R.
![]()
Figure 10. The temperature distribution for different values of Pr.
![]()
Figure 11. The temperature distribution for different values of![]() .
.
increase when the internal heat generation parameter ![]() becomes stronger whereas the internal heat absorption parameter
becomes stronger whereas the internal heat absorption parameter ![]() have the opposite effect. Also, we can note that the highest temperature distribution for fluid in boundary layer was obtained with the greatest heat generation parameter
have the opposite effect. Also, we can note that the highest temperature distribution for fluid in boundary layer was obtained with the greatest heat generation parameter![]() . Likewise, it is shown that the effect of
. Likewise, it is shown that the effect of ![]() causes a drop in the temperature distribution as the heat following from the sheet is absorbed.
causes a drop in the temperature distribution as the heat following from the sheet is absorbed.
Table 3 shows the influence of the magnetic parameter M, wall thickness parameter![]() , the velocity power index parameter m, the radiation parameter R, the Prandtl number Pr, the heat generation/absorption parameter
, the velocity power index parameter m, the radiation parameter R, the Prandtl number Pr, the heat generation/absorption parameter ![]() and the thermal conductivity parameters
and the thermal conductivity parameters ![]() on the local skin friction coefficient and the local Nusselt number. It is noticed that increases in the wall thickness parameter leads to an increase in both the local skin-friction coefficient and the local Nusselt number. Likewise, the local Nusselt number is reduced but the skin-friction coefficient is increased with increasing for both values of magnetic parameter and velocity power index parameter. Also, an increase in the Prandtl number causes an increase in the local Nusselt number. This is because a fluid with larger Prandtl number possesses larger heat capacity, and hence intensifies the heat transfer. On the other hand, as it is observed the local Nusselt number decreases with increasing
on the local skin friction coefficient and the local Nusselt number. It is noticed that increases in the wall thickness parameter leads to an increase in both the local skin-friction coefficient and the local Nusselt number. Likewise, the local Nusselt number is reduced but the skin-friction coefficient is increased with increasing for both values of magnetic parameter and velocity power index parameter. Also, an increase in the Prandtl number causes an increase in the local Nusselt number. This is because a fluid with larger Prandtl number possesses larger heat capacity, and hence intensifies the heat transfer. On the other hand, as it is observed the local Nusselt number decreases with increasing![]() , while they increases with increasing
, while they increases with increasing![]() . Moreover, it is observed that the values of the local Nusselt number decreases with increase in both the thermal conductivity parameter and the radiation parameter.
. Moreover, it is observed that the values of the local Nusselt number decreases with increase in both the thermal conductivity parameter and the radiation parameter.
5. Conclusion
In this work, we implemented the Chebyshev spectral method to solve the non-linear system of ODEs of the proposed model. The fluid thermal conductivity is assumed to vary as a linear function of temperature. Asystematic study on the effects of the various parameters on flow and heat transfer characteristics is carried out. It has found that the effect of increasing values of the magnetic parameter, the velocity power index parameter, thermal conductivity parameter and the radiation parameter reduce the local Nusselt number. On the other hand, it is observed that the local Nusselt number increases as the Prandtl number and wall thickness parameter increases. Moreover, it is interesting to find that as the magnetic parameter, wall thickness parameter and the velocity power index parameter increases in magnitude, causes the fluid to slow down past the stretching sheet, the skin-friction coefficient increases in magnitude. A comparison with previously published work is given to ensure that the obtained numerical results are in excellent agreement, and this confirms that the validity of the proposed method to solve the presented model. Finally, we can make the error is smaller by increasing the terms in the series (27). All computations in this paper are done using Mathematica 8.
Acknowledgements
The first three authors thank Deanship of Academic Research, Al Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, KSA, for the financial support of the project number (351227).