A Two-Point Boundary Value Problem by Using a Mixed Finite Element Method

Pedro Pablo Cárdenas Alzate, José Rodrigo González Granada

Department of Mathematics, Universidad Tecnoloacute;gica de Pereira, Pereira, Colombia.

DOI: 10.4236/am.2015.612177                

Abstract

This paper describes a numerical solution for a two-point boundary value problem. It includes an algorithm for discretization by mixed finite element method. The discrete scheme allows the utilization a finite element method based on piecewise linear approximating functions and we also use the barycentric quadrature rule to compute the stiffness matrix and the L₂-norm.

Keywords

Two-Point BVP, Galerkin’s Method, Non-Symmetric Problem

1. Introduction

Finite element methods in which two spaces are used received the domination of mixed finite element method. Sometimes a second variable is introduced in the formulation of the problem by its physical study, for example in the case of elasticity equations and also the Stokes equations where the mixed formulation is the natural one. The mathematical analyses of mixed finite element have been widely developed in the seventies. A general analysis was first developed by [1] . We also have to mention to [2] and [3] which introduced of the fundamental ideas for the analysis of mixed finite elements. We also refer to [4] and [5] where general results are obtained.

An outline of the paper is as follows. We derive the mixed variational formulation for bilinear form non- symmentric problem and we define the related discrete elements and the error analysis of the associated finite element method is made [6] . We generalize the results to mixed methods using rectangular elements and we use the barycentric quadrature rule to compute the stiffness matrix, the load vector and the L₂-norm. Finally, numerical experiments are given to illustrate the present theory [7] .

2. Error in the Finite Element Solution

Recall that 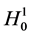in one dimension by Sobolev’s inequality, so that 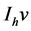is defined for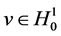. We can prove that with 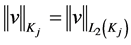and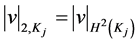

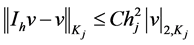
and

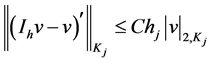
In fact, by definition we have

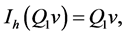(1)

where 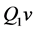is the polynomial of degree 1 approximating v in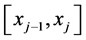, then we have

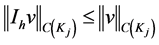
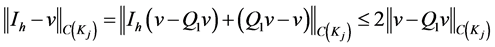
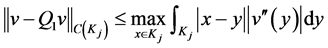
therefore, the error is of order 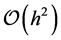because the fitting is until the second derivative, then

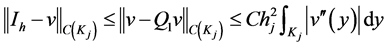
Now, we know that

So, we can write as

then we obtain

So

To write the norm in, fort take square

Next, integrate with respect to we have:

Taking the square root finally we obtain

3. Galerkin’s Method

Galerkin’s method: Let and satisfy the assumptions of the Lax-Milgram lemma

and be the solution of. Let be a finite-dimensional subspace and be determined by Galerkin’s method: for all. We want to prove that

(2)

and with symmetric,

(3)

(4)

In fact, let and with and. Thus,

Now, from the assumptions of the Lax-Milgram lemma we have

(5)

. And

Divide by both sides we have

Now, using (5), we get that

Finally, we can prove (4)

Now, for the symmetric we can apply Riesz representation theorem. Therefore the norm of the inner product can be written as

Similar to previous proof, we have

Therefore

As for the norm in V, we have

(6)

From the assumptions we obtain

With and we have

Using this inequality, (6) becomes

We know that

from Equation (4) which was proven in the previous section, therefore

4. FEM for Bilinear Form Non-Symmetric Problem

We consider the problem

in with on. A finite element method for this problem with an error bound in the -norm is as follows. First we need to find the variational formulation for this problem. In fact, multiply by a function on:

Next, integrate over the domain:

Now, the left hand side can be written using integrating by parts:

Therefore we have the bilinear form

and the linear functional

The space is dense in and by Lax Milgram theorem, there is a weak solution in. is coercive in, therefore

The bilinear form is also bounded:

Now, we would like to minimize the residual

Also we have (see [2] )

where. Therefore, we can apply the previously proven statement (2) in order to estimate a bound for the error

which for our case become

5. BVP by Finite Element Method

We consider the boundary value problem

Figure 1. Mesh used to solve the problem (7) by using (8).

Figure 2. (a) Solution of the system (7) using; (b) Error of the approximation in (a), compared to the real solution; (c) Solution of the system (7) using; (d) Error of the approximation in (b), compared to the real solution.

Figure 3. Logarithmic plot of the L₂-norm of the error vs. the choice of h.

(7)

We want to solve it by the finite element method

(8)

based on piecewise linear approximating functions on the partition, divided into triangles by inserting a diagonal with positive slope into each mesh-square with. We will use the barycentric quadrature rule to compute the stiffness matrix, the load vector and the L₂-norm. The Figure 1 shows the mesh used to solve this problem (system (7)). With this mesh, the stiffness matrix A was computed considering each node, from a total of interior nodes (, which h is the step size). The basis function is a set of pyramidal functions. At each node, there are two triangles coming at a straight angle, and four others coming with an acute angle. The basis functions are therefore

Therefore we obtain

・ . There are two triangles common to these neighboring nodes, therefore this inner product is. It is the same for the neighbours on the left (2 common triangles). Similarly for the neighbours on the rows above and below. This inner product was used in the stiffness matrix A.

・ The Barycentric Quadrature Rule were used to evaluate the integral on the right hand side,

where

where K is each triangle in the mesh, the vertices.

・ Figure 2 shows the solution of (7) for (panel A) and (panel C). Compared to the correct solution

the errors are shown in (panel B) and (panel C) respectively.

・ norm of this error is shown Figure 3.

Acknowledgments

We thank the editor and the referee for their comments and group GEDNOL of the Universidad Tecnológica de Pereira-Colombia.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Brezzi, F. (1974) On the Existence, Uniqueness and Approximation of Saddle Points Problems Arising from Lagrangian Multipliers. ESAIM: Mathematical Modelling and Numerical Analysis—Modélisation Mathématique et Analyse Numérique, 8, 129-151.
[2]	Larsson, S. and Thome, V. (2009) Partial Differential Equations with Numerical Methods. Springer-Verlag, New York.
[3]	Canuto, C. and Hussaini, M. (1988) Spectral Methods in Fluids Dynamics. Springer Series in Computational Physics, Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-84108-8
[4]	Fortin, M. (1977) An Analysis of the Convergence of Mixed Finite Element Methods. R.A.I.R.O, 11, 341-354.
[5]	Guzman, J. (2010) A Unified Analysis of Several Mixed Methods for Elasticity with Weak Stress Symmetric. Journal of Scientific Computing, 4, 156-169. http://dx.doi.org/10.1007/s10915-010-9373-2
[6]	Yao, C. and Jia, S. (2014) Asymptotic Expansion Analysis of Nonconforming Mixed Finite Element Methods for Time-Dependent Maxwell’s Equations in Debye Medium. Applied Mathematics and Computation, 229, 34-40. http://dx.doi.org/10.1016/j.amc.2013.12.016
[7]	Pal, M. and Lamine, S. (2015) Validation of the Multiscale Mixed Finite-Element Method. International Journal for Numerical Methods in Fluids, 77, 206-223. http://dx.doi.org/10.1002/fld.3978