Modeling of Infiltration Characteristics by Modified Kostiakov Method ()
1. Introduction
Infiltration may be defined as the intake of water into the soil profile. The rate and cumulative infiltration amount are necessary to calculate the total water requirement for efficient irrigation system [1] . Infiltration is one of the most important components of hydrologic cycle. As the duration of rainfall continues to increase, the soil becomes increasingly saturated resulting in a decrease in infiltration capacity [2] . Consequentially, the excess rainfall from the infiltration process starts surface ponding in surface depressions which leads to surface runoff [3] . Irrigation scheduling involves two main considerations. They are 1) when to apply water, and 2) how much water to apply. Ensuring the answers of these two issues is very important for best crop and water management practices [1] . In different developing or underdeveloped countries, measurement of infiltration is not practiced or even shows any interest of measuring it. There are several reasons for this:
- lack of awareness of measuring actual volume and rate of infiltration;
- lack of skill and knowledge of infiltration measurement and its role in water management practices.
Considering the importance and economic benefit of irrigation and water management practices, a mathematical model may be prepared and available for serving the assessment and quantifying the amount of water needed for actual water requirement of the crops [1] .
2. Factors Involving in Infiltration Rate
Infiltration capacity is dependent on soil texture, soil structure, and soil cover. Also, infiltration is dependent on existing soil moisture content, soil hydraulic conductivity, soil porosity, existing soil swelling colloids and organic matters, irrigation or rainfall duration, and viscosity of water [4] . For irrigating the crops, how much water needs to be applied to reach the water requirement by the crop needs, the information of infiltration and accordingly apply that amount of water for maximum water application and use efficiencies. Infiltration has the unit of velocity, like cm/hour. From this definition, it is well understood that the distance or height of entrance of water per unit time is dependent of soil characteristics. Compactness of soil, porosity, and soil type play a vital role to allow the water to enter and flow downward. Moreover, if the antecedent moisture content is already enough in the soil profile, there will be a less opportunity of the incoming water to get into the soil profile. Water will infiltrate until the water has enough space in the soil profile or if the soil becomes saturated, the excess water will start filling up the soil depressions and finally runoff will take place following the surface gradient into the nearest reservoir.
3. Methods of Measuring Infiltration
There are three methods for determining the infiltration characteristics for any irrigation system design and water management practices. They are: 1) cylindrical infiltrometer method, 2) Accumulation infiltration estimation from waterfront advance data, and 3) Depletion of free water surface measurement in a large basin.
Out of the above mentioned methods, cylindrical infiltrometer method is most commonly used. Cylindrical infiltrometer method offers the advantages over the other two avoiding the cumbersome procedure in collecting correct data from the field while estimating from waterfront advance data and there is necessity of considering the evaporation loss due to atmospheric influences on the large basin while measurement of water depletion is considered [3] . Hence, the cylindrical infiltrometer is comparatively reliable for measuring the infiltration rate and accumulated infiltration. Infiltration characteristics can be measured by using a metal cylindrical round shaped hollow drum driven to a certain length into the soil surface and then ponding this cylinder with water and simultaneously record the time required to deplete water and enter into the soil surface. In early days, only one cylinder was used to measure the height of water lowered in the cylinder. That procedure yielded several drawbacks and a higher degree of variability due to the uncontrollable movement of lateral seepage and movement of water to and from the cylinder. This lateral movement of water has been well controlled by another concentric cylinder similarly with ponded water as the inner cylinder.
Figure 1 shows the dimensions of a common Infiltrometer. There are two cylinders of diameters 30 cm and the 60 cm are driven concentrically into the soil surface about 10 cm and the total height of these two ring cylinders is 25 cm.
The material used for making these cylinders is of 2 mm rolled steel. The inner and the outer cylinders are both ponded with water. The outer cylinder is used as a buffer pond to avoid the lateral movement of water from and to the inner cylinder. Care should be taken against beveling of the cylinder bottoms. The cylinders are driven into the soil by a falling weight hammer striking on top of a wooden plank placing on top of the cylinders to avoid the damage at the edge of the cylinders.
The main objective of this study was to develop a model for infiltration characteristic by modified Kostiakov method and to calculate the accumulated infiltration and infiltration rate with specific focus on: 1) deriving the constant values of modified Kostiakov method for the soil under consideration, 2) judging the applicability of the model using the field data, and 3) find the percentage of error between the actual and the values calculated by the model.
![]()
Figure 1. Plan and cross-sectional views of a cylindrical infiltrometer.
4. Methodology
This study was carried out in the Irrigation and Water Management demonstration field of BARI in 2012. This field is used for demonstration purposes and to exhibit different irrigation methods for training the farmers and agricultural extension officials. Sometimes, these plots are used for both exhibition and crop related research purposes too. The field was kept fallow at the time when the study was conducted. It was clay-loamy soil, without any tillage practices done and had common soil vegetation. Four infiltrometers were installed lengthwise with distances as shown in Figure 2.
The water levels of the inner cylinder were read by a needle type pointed hook gage whose sharp and pointed headend was just touching water level for initial water height reading and the tail end was set with a scale to read the difference after a predetermined time when a depletion of water height was there by adjusting the pointed head again touching the depleted water surface. The difference between initial and the final readings were the height of water that infiltrated during the predetermined time. This height divided by time is the one what is defined as the infiltration rate. Here times were recorded as minutes but they were converted into hours for calculation purposes and express the infiltration rate as cm/hr. After some period, there is no more depletion of water took place and the curve of accumulated infiltration (ordinate) vs. time (abscissa), is the constant infiltration rate the characteristic of this point and hereafter is called asymptote. At the initial stages, time vs. depletion of water recordings were taken frequently, refill of water were done as quickly as possible so that the pace of infiltration could be kept constant. Water levels in the inner and the outer cylinders were kept approximately same to keep up the water pressures same between the inner and outer cylinders and avoids the lateral water movement due to dissimilar height between the inner and the outer cylinders. The average values of accumulated infiltration y and average infiltration rate have been plotted against time t and shown in Figure 3.
The modified Kostiakov method [1] was tested if it suits the local soil condition and if it can be represented for the accumulated infiltration and infiltration rate. The relationship of accumulated infiltration y with respect
![]()
Figure 2. Field layout with the locations of the infiltrometers.
![]()
Figure 3. Average infiltration rate (cm/h) and accumulated infiltration (cm) vs. time (min).
to time t can be mathematically defined by the following equation, known as modified Kostiakov method:
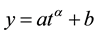 (1)
(1)
where
y = accumulated infiltration at time t, (cm),
t = elapsed time, (min), and
a, α, and b are three characteristic constants.
Values of a, α, and b can be calculated by the method suggested by Davis [5] . Values of a, α, and b are usually less than 1 [1] . The steps are described below:
1) plot the values of y and t;
2) select a pair of points of (t1, y1) and (t2, y2) from this plot, selection of the points on the plotted line should be near the extremities of the line to cover a wide range of interpolated values;
3) calculate a third value for time t3 using the values of t1 and t2 from the procedure followed in the previous step. The equation for calculating t3 is as follows:

Values of t1 and t2 are available from the plotted line and that has been described in step 2.The corresponding value of accumulated infiltration y3 = 5.9 cm when t3 = 25.5 minutes. Value of b can be calculated by formula used in regression analysis. The formula can be shown as follows (refer to Figure 4):
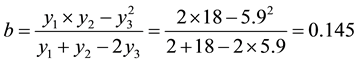
Equation (1) can be rearranged and written as
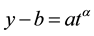 (2)
(2)
Taking log both sides
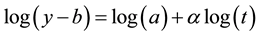 (3)
(3)
Table 1 shows the calculated values of the accumulated infiltration y in cm and their corresponding time t in minute for infiltrometers 1 and 2 and the same is represented in Table 2 for Infiltrometer 3 and 4. Table 3 shows the average values of accumulated infiltration, infiltration rate vs. time for Infiltrometer 1, 2, 3, and 4. These values are used to plot the accumulated infiltration.
Equation (3) yields the following equations when the values of b and t are substituted:
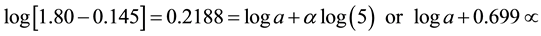 (4)
(4)
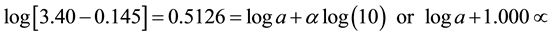 (5)
(5)
 (6)
(6)
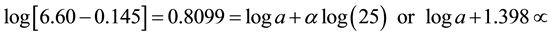 (7)
(7)
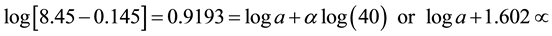 (8)
(8)
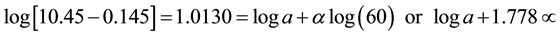 (9)
(9)
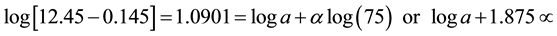 (10)
(10)
![]()
Figure 4. Accumulated infiltration versus time in log scale.
![]()
Table 1. Field trials of cylindrical infiltrometer, accumulated infiltration, infiltration rate vs. time for infiltrometer 1 and 2.
![]()
Table 2. Field trials of cylindrical infiltrometer, accumulated infiltration, infiltration rate vs. time for infiltrometer 3 and 4.
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
Adding Equations (4) to (8)
![]() (14)
(14)
Adding Equations (9) to (13)
![]() (15)
(15)
Solving Equations (14) and (15), the value of α becomes 0.683
The value of ![]()
Now substituting the values of a, b, and α in equation for individual elapsed times
![]()
At t = 5 min, ![]()
![]() (16)
(16)
At t = 10 min, ![]()
![]() (17)
(17)
At t = 15 min, ![]()
![]() (18)
(18)
At t = 25 min, ![]()
![]() (19)
(19)
At t = 40 min, ![]()
![]() (20)
(20)
At t = 60 min, ![]()
![]() (21)
(21)
At t = 75 min, ![]()
![]() (22)
(22)
At t = 90 min, ![]()
![]() (23)
(23)
At t = 110 min, ![]()
![]() (24)
(24)
At t = 130 min, ![]()
![]() (25)
(25)
5. Results and Discussions
The percentage of error was calculated by the following equation:
![]() (26)
(26)
where, ![]() is the actual accumulated infiltration,
is the actual accumulated infiltration, ![]() calculated accumulated infiltration by the model, i is the number of data.
calculated accumulated infiltration by the model, i is the number of data.
Table 4 shows the percentage of error between the actual and calculated values of accumulated infiltration with respect to time. The average value of percentage of error was 0.134 which is significantly lower range of acceptability. Figure 5 also shows very good agreement between the actual and calculated values of accumulated infiltration. Individual error was calculated to see the deviation of the accumulated infiltration. The lowest value was only −0.71 and the highest value was 18.72 percent. Values of log (a), α, and b were 0.178, 0.683, and
![]()
Table 3. Average values of accumulated infiltration, infiltration rate vs. time for Infiltrometers 1, 2, 3, and 4.
![]()
Table 4. Percentage of error between the actual and calculated values of accumulated infiltration vs. time.
*Average of 1 to 4 infiltrometer reading; **Equations (16) to (25).
0.145, respectively, which are below 1 and follows and maintains the requirement of the modified Kostiakov method [1] .
Figure 4 and Figure 5 show very good agreements of the model values with the actual data from the field. Therefore, this model can be a very good tool to determine the infiltration rate and accumulated infiltration of the field. This will also be a good representative of the infiltration characteristic of the site. This information can be valued asset for irrigation scheduling for any crop cultivated in that field to ensure the best water management practices.
6. Conclusion
This model is developed to estimate the rate and accumulated infiltration of water in agricultural land is using
![]()
Figure 5. Observed and calculated accumulated infiltration vs. time.
modified Kostiakov method. Values for a, α, and b of modified Kostiakov equation are calculated to be 0.178, 0.683, and 0.145, respectively, which are below 1. This condition follows the principle of modified Kostiakov method [1] . It shows a good agreement between the model and the calculated values of the rate and accumulated infiltration. The percentage of error is 0.134 which is very promising. The characteristics constant values of modified Kostiakov equation are also determined and found to be within the acceptable ranges. One can easily identify the rate and the accumulated infiltration once the graphical results are produced. Also, this model will require no technical background for the users.
Acknowledgements
The authors would like acknowledge Prof. Rao Mentreddy and Prof. Michael Ayokanmbi of Alabama Agricultural and Mechanical University for reviewing this manuscript and making valuable suggestion.
NOTES
*Corresponding author.