Global Stability of SEIQRS Computer Virus Propagation Model with Non-Linear Incidence Function ()
1. Introduction
The Malicious objects are harmful codes that reproduce and spread by way of internet [1] . A number of malicious objects have been noticed to appear on the internet for the last decade. They are powerful enough to confront and disfunction the infected computer system. As the internet has been used for a wide range of function so, the malicious objects have become a serious threat to man’s work. They have hampered the economic and financial growth of man. Now it has become an issue of great concern and therefore it is vital to suggest such plans that are effective in combating the malicious objects. The correspondence between the propagation of biological virus and the malicious objects compel the researchers to advocate epidemic models that could explain and overcome the propagation of malicious objects. Re F. Wang et al. in [2] present the SEIQRS model with graded infection rates for internet worms. The infection ratio of exposed class have less then infected ratio and show the worm free and viral equilibrium stability locally as well as globally, which is connected to threshold quantity. In the previous decade or something like that, various epidemic models (see [3] - [6] ) were essentially obtained to depict the spread of computer virus. B. K. Mishrand G. M. Ansari present an E-SIRS epidemic model for virus and worms in a computer network. In which they consider the immune as well as the latent period and self-replication time. They stated the global stability of the proposed model in term of reproduction number [7] . M. Kumar et.al. studied the quarantine and vaccination role in the control of virus and worms in the computer network [8] . S. T. Ge et al. presented the SEIQR epidemic model with the discrete time in computer networks. The stability of the proposed model was shown by Lyapunove method in [9] . M. Kummar and A. Kumar analyzes the SIj RS E-Epidemic model for various groups of infection in computer networking [10] .
In this paper, we present a Propagation Model with non-linear incidence function, (susceptible, exposed, infected, quarantined, and recovered) which exhibits two equilibria the virus free and viral equilibrium point. The stability of both equilibrium points is connected with the threshold quantity. On the off chance that its value is less then unity then the virus free equilibrium point is locally and additionally globally asymptotically stable and in the opposite case of the threshold quantity, the same condition of stability is satisfied for viral equilibrium point.
The rest of the paper is set as follows, in Section 2 we shall formulate the new model, in Section 3 the basic propertied is discussed like reproduction number, virus free and viral equilibrium. In Section 4, we shall study the local and global stability of the virus free equilibrium point. In Section 5, we shall examine the local and global stability at viral equilibrium point. Finally, we support our analytical work with numerical simulations.
2. Model Formulation
As usual the computer it either internal or external (i.e. connected with the internet or not). In this model we divide the internal computers into five states. Susceptible, exposed, infected, quarantined and recovered. Where the variable S(t), E(t), I(t), Q(t) and R(t) denote the sizes of nodes at time t in the states susceptible, exposed, infectious, quarantined and recovered respectively. N(t) the total number of computer at time t, where N(t) = S(t) + E(t) + I(t) + Q(t) + R(t). The governed model is given below:
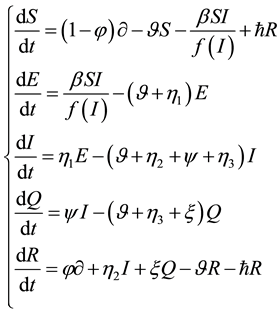 (1)
(1)
With Initial conditions
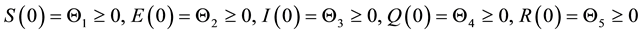 (2)
(2)
where  is the recruitment rate of the computers. The ratio of crashing nodes without attack of malicious objectsis
is the recruitment rate of the computers. The ratio of crashing nodes without attack of malicious objectsis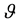 . The transmission rate is denoted by
. The transmission rate is denoted by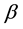 . While
. While 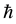 is the ratio at which the recovered computers loss their immunity. The contact ratio between exposed and infected computers is
is the ratio at which the recovered computers loss their immunity. The contact ratio between exposed and infected computers is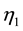 . The rate of recovery is
. The rate of recovery is  and
and 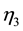 is the contact ratio between infected and recovered computers.
is the contact ratio between infected and recovered computers. 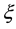 is the contact ratio between infected and recovered computers.
is the contact ratio between infected and recovered computers.  is the fraction of computers to be immune from virus.
is the fraction of computers to be immune from virus.
We suppose that the like transmission rate in the form of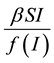 , where f is a positive function with,
, where f is a positive function with,  and
and , used by [11] . This is the generalized form of mass action law, that is,
, used by [11] . This is the generalized form of mass action law, that is,  , and the incidence rate
, and the incidence rate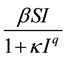 . The function
. The function ![]() is increasing for small values of I and decreasing in the opposite case where
is increasing for small values of I and decreasing in the opposite case where![]() .
.
3. Basic Reproduction Number and Equilibrium Points
In this subsection, we shall investigate the feasible region and the threshold quantity for the proposed model (1). Where the size of total population is represented by N satisfy the following equation.
![]()
and then
![]()
Therefore, for the system (1) the positively invariant feasible region is given below.
![]() ,
,
Thus, the solution with initial condition will be analyzes inside the feasible region![]() .
.
For viral free equilibrium point we take![]() , thus from the system (1) we get
, thus from the system (1) we get
![]() .
.
To investigate the reproduction Number for system (1) we use the next generation method [12] .
Assume that ![]() then from system (1) we can write.
then from system (1) we can write.
![]()
where
![]()
![]()
![]()
![]()
![]()
The spectral radius of the matrix ![]() is represented by
is represented by ![]()
![]()
Now we examine the virus equilibrium point for the given system (1) and denoted by
![]()
where
![]() ,
,
![]() ,
,
Now by substituting the above mention values of![]() , in equation
, in equation
![]()
we get
![]()
When![]() ,
, ![]() is non-negative then
is non-negative then ![]() is a decreasing function Moreover.
is a decreasing function Moreover.
![]()
![]() (3)
(3)
Next to take the derivative of![]() .
.
![]()
Since ![]() and
and ![]() also for
also for![]() ,
, ![]() is follows that
is follows that
![]()
Therefore, ![]() has a unique positive zero if and only if
has a unique positive zero if and only if![]() , i.e.
, i.e.![]() . It can be stated as below.
. It can be stated as below.
Proposition 3.1. Suppose that ![]() holds the conditions imposed on it. Then, the system (1) has virus free equilibrium point
holds the conditions imposed on it. Then, the system (1) has virus free equilibrium point ![]() which is true for all parameter values. When, the system (1) admits also a unique viral equilibrium point
which is true for all parameter values. When, the system (1) admits also a unique viral equilibrium point![]() .
.
4. The Stability Analysis of the Virus Free Equilibrium Point
In this section, we shall study the local and global stability of the given system (1) at virus free equilibrium point![]() .
.
Theorem 4.1. The given system (1) is locally asymptotically stable if![]() , otherwise unstable.
, otherwise unstable.
Proof:
To examine the local stability of the given system (1) we construct the jacobian matrix at![]() , which is given below.
, which is given below.
![]()
![]()
With row operation we can get the characteristic equation of the above jacobian matrix is
![]()
The first three roots of the above equation is ![]() and the other roots will be find on the following way.
and the other roots will be find on the following way.
![]()
After a little algebraic calculation we can get the following equation
![]()
where
![]()
![]()
![]() and
and ![]() if
if ![]() then according to Routh-Hurtwiz criteria the virus free equilibrium point
then according to Routh-Hurtwiz criteria the virus free equilibrium point ![]() is locally asymptotically stable. If
is locally asymptotically stable. If ![]() then
then ![]() and hence one of the eigenvalue have positive real part. So the virus free equilibrium point is unstable.
and hence one of the eigenvalue have positive real part. So the virus free equilibrium point is unstable.
Global Stability of Viral Free Equilibrium Point
Theorem 4.2. The system (1) at ![]() is globally stable when
is globally stable when ![]() otherwise unstable.
otherwise unstable.
Proof: To examine the global stability of the proposed model consider a Lyapunov function as below:
![]()
Taking the derivative i.e.![]() , we get the following
, we get the following
![]()
Since for ![]() and after a little simplification we get the following results
and after a little simplification we get the following results
![]()
![]() if
if ![]() and
and ![]() then according to Lasalle’s invariance principle the virus free equilibrium point
then according to Lasalle’s invariance principle the virus free equilibrium point ![]() is globally stable and in case of
is globally stable and in case of ![]() the mention result is failed and hence the system is unstable [13] .
the mention result is failed and hence the system is unstable [13] .
5. The Local Stability Analysis of Viral Equilibrium Point
In this section we will discuss the local as well as the global stability of the system (1) for the viral equilibrium point.
Theorem 5.1. The given system (1) at ![]() is locally asymptotically stable if
is locally asymptotically stable if![]() .
.
Proof: Toinvestigate the local stability of the given system (1) we find the jacobian matrix at![]() , which is given below.
, which is given below.
![]()
![]()
Trace of the above jacobian Matrix ![]() is
is
![]()
And after some row operation we get the following matrix ![]()
![]()
![]()
Thus, the system (1) at ![]() has eigenvalues, that contains negative real part. So, we conclude that the model (1) is locally asymptotically stable.
has eigenvalues, that contains negative real part. So, we conclude that the model (1) is locally asymptotically stable.
Global Stability of Viral Equilibrium Point
In this segment we should look at the global stability of the given system (1) at viral equilibrium point. We use the method presented in [14] established by Li and Mouldowney. According to which we find sufficient condition for the global stability of the model (1) at viral equilibrium point. First we shall discuss the method briefly.
Consider
![]() (4)
(4)
where ![]() is simply connected, open set and
is simply connected, open set and![]() . The solution of Equation (4) is denoted by
. The solution of Equation (4) is denoted by ![]() Let us suppose that the assumptions given below are true:
Let us suppose that the assumptions given below are true:
・ ![]() There exist a compact absorbing set
There exist a compact absorbing set ![]()
・ ![]() Equation (4) admit a unique equilibrium
Equation (4) admit a unique equilibrium ![]()
We know that equilibrium point ![]() is globally stable in
is globally stable in ![]() when it locally stable as well as all the orbits in
when it locally stable as well as all the orbits in ![]() converges to
converges to![]() . Bendixson criterion for
. Bendixson criterion for ![]() we mean that
we mean that ![]() satisfied a condition which prohibit the existence of non-constant periodic solutions of (4) The classical Bendixson’s condition
satisfied a condition which prohibit the existence of non-constant periodic solutions of (4) The classical Bendixson’s condition ![]() for
for![]() , is robust under
, is robust under ![]() robust properties are discussed in [14] [15] .
robust properties are discussed in [14] [15] .
If a neighborhood ![]() exist for
exist for ![]() for
for ![]() such that i.e.
such that i.e. ![]() Then the point
Then the point ![]() is wandering for the Equation (4). The following principle for global stability is established in [14] for any finite dimension autonomous systems.
is wandering for the Equation (4). The following principle for global stability is established in [14] for any finite dimension autonomous systems.
Lemma 5.1. Assume that conditions ![]() and
and ![]() holds. Such that (4) satisfies a Bendixson criterion that is robust under
holds. Such that (4) satisfies a Bendixson criterion that is robust under ![]() local perturbations of
local perturbations of ![]() at all non-equilibrium non-wandering points for (4). Then
at all non-equilibrium non-wandering points for (4). Then ![]() is globally stable in
is globally stable in ![]() provided it is stable.
provided it is stable.
The accompanying Bandixson criterion is displayed in [14] and indicates to have the heartiness needed by Lemma (5.1). Let ![]() be a nonsingular matrix and
be a nonsingular matrix and ![]() is a matrix valued function that
is a matrix valued function that ![]() on
on![]() . Suppose that for a compact absorbing set
. Suppose that for a compact absorbing set ![]() not only exist but also continues for
not only exist but also continues for![]() . A
. A ![]() quantity is defined as.
quantity is defined as.
![]()
where
![]()
The matrix ![]() is
is
![]()
And ![]() represents the second additive compound matrix of the Jacobian matrix J, i.e.,
represents the second additive compound matrix of the Jacobian matrix J, i.e.,![]() . Let
. Let ![]() and
and ![]() be the Lozinskii measure of
be the Lozinskii measure of ![]() with respect to a vector norm
with respect to a vector norm ![]() in
in![]() ,
,
![]()
It is shown in [14] that, if ![]() is simply connected, the condition
is simply connected, the condition ![]() rules out the presence of any trajectory that fives rise to a simple closed rectifiable curve, like periodic orbits, and heteroclinic cycles it is invariant for system (4). The accompanying result for the global stability is displayed in [14] by Li and Muldowney.
rules out the presence of any trajectory that fives rise to a simple closed rectifiable curve, like periodic orbits, and heteroclinic cycles it is invariant for system (4). The accompanying result for the global stability is displayed in [14] by Li and Muldowney.
Lemma 5.2. Let the simply connected set ![]() satisfy the conditions
satisfy the conditions ![]() and
and![]() . Then the system (4) is globally stable in
. Then the system (4) is globally stable in ![]() at a unique equilibrium
at a unique equilibrium ![]() if
if![]() .
.
Now for the analysis of global stability at viral equilibrium we follow the method presented by Li and Muldowney in [14] . The unstable viral equilibrium point ![]() means that the viruses will persists [16] , i.e., for any solution
means that the viruses will persists [16] , i.e., for any solution ![]() with initial conditions
with initial conditions ![]() in the trajectory of the model (1) there exist a constant
in the trajectory of the model (1) there exist a constant ![]() which satisfy the following
which satisfy the following
![]()
Theorem 5.2. The viral equilibrium ![]() of the system (1) is globally stable in
of the system (1) is globally stable in ![]() if
if![]() .
.
Proof: For the global stability of the system (1) we find the second additive compound matrix ![]()
![]()
![]()
Let us choose a function![]() .
.
Then,
![]()
![]()
So,
![]()
Therefore,
![]()
![]()
Let
![]()
where,
![]()
![]()
![]()
![]()
Suppose the norm in ![]() as:
as:
![]()
where ![]() be the vector in
be the vector in ![]() and
and ![]() signify the Lozinskii measure as regard to this norm follows [17] .
signify the Lozinskii measure as regard to this norm follows [17] .
![]()
where,
![]()
![]()
Therefore,
![]()
using second equation of system (1) ![]()
![]()
![]()
Again,
![]()
where,
![]()
And ![]()
![]()
using third equation of system (1), ![]()
![]()
![]()
With a compact absorbing set ![]() every solution
every solution ![]() of the model (1) with
of the model (1) with ![]() we have
we have
![]()
![]()
Thus the viral equilibrium ![]() is globally asymptotically stable according to [14] .
is globally asymptotically stable according to [14] .
Next we talk about the given subsystem of system (1)
![]() (5)
(5)
And it limit system is
![]() (6)
(6)
Based on (6), we get
![]()
![]()
This implies that as ![]() then
then
![]()
Then according to [18] the system (1) at ![]() is globally asymptotically stable.
is globally asymptotically stable.
6. Discussion
The aim of this work is to study and analyze the dynamic behavior of an epidemic model SEIQRS with a nonlinear incidence function. We consider a mathematical model of the type SEIQRS and obtained the basic reproduction number, to determine its dynamical behavior. In epidemiology, the reproduction ratio is very important, because the stability of the proposed model is associated with reproduction ratio. For virus free equilibrium point, the model is stable locally and globally if![]() . In the case of when
. In the case of when ![]() exceeds then unity then the system (1) is asymptotically stable at viral equilibrium point.
exceeds then unity then the system (1) is asymptotically stable at viral equilibrium point.
The purpose of this section is to support the analytic results mentioned in above work are supported through numerical results. Numerical results we choose different values of parameters, which we discuss below with the help of graph. For![]() , the reproduction ratio for immune free system is
, the reproduction ratio for immune free system is
![]()
Thus we can write ![]() is
is
![]()
If![]() , then clearly the virus is vanished. But if
, then clearly the virus is vanished. But if ![]() (see Figure 1), then the vaccination
(see Figure 1), then the vaccination ![]() is needed so that
is needed so that ![]() or equivalently to
or equivalently to![]() .
.
Thereby, ![]() is the vaccination able to exterminate the virus from the internal computers Figure 2 and Figure 3. In the opposite case
is the vaccination able to exterminate the virus from the internal computers Figure 2 and Figure 3. In the opposite case![]() , the virus will persists, even if we can vaccinate all recruitment Figure 4.
, the virus will persists, even if we can vaccinate all recruitment Figure 4.
Nothing that when![]() , since
, since ![]() is an increasing function of
is an increasing function of![]() , and the value of the vaccination cover
, and the value of the vaccination cover
![]()
Figure 1. The dynamical behaviour of system (1), for different initial conditions and parameters: ∂ = 5, ϑ = 0.05, β = 0.02, ћ = 0.02, η1 = 0.009, η2 = 0.001, η1 = 0.03, ξ = 0.01, ψ = 0.01, φ = 0, Here![]() , R1 = 1.9068.
, R1 = 1.9068.
![]()
Figure 2. The dynamical behaviour of system (1), for different initial conditions and parameters of Figure 1 except φ = 0.6 < φv = 0.6658.
![]()
Figure 3. The dynamical behaviour of system (1), for different initial conditions and parametes of Figure 1 except φ = φv = 0.6658.
![]()
Figure 4. The dynamical behaviour of system (1), for different initial conditions and parametes ∂ = 8, ϑ = 0.03, β = 0.02, ћ = 0.02, η1 = 0.009, η2 = 0.01, η1 = 0.03, ξ = 0.01, ψ = 0.01, φ = 1. Here![]() , φv = 1.5150.
, φv = 1.5150.
age ![]() exceed then unity when
exceed then unity when![]() . Therefore, for the reduction of vaccination coverage it is important through vaccination
. Therefore, for the reduction of vaccination coverage it is important through vaccination ![]() increase the time period of the loss of immunity.
increase the time period of the loss of immunity.
Acknowledgements
The author is grateful to the anonymous reviewers for their constructive suggestions that greatly improve the quality of this paper.