A Finite-Dimensional Integrable System Related to the Complex 3 × 3 Spectral Problem and the Coupled Nonlinear Schrödinger Equation ()
1. Introduction
As is well known, the technique of the nonlinearization of Lax pairs has been a powerful tool for the finding of integrable systems in the last two decades or so. With this technique, the representation of the solution to the systems can also be generated. A lot of researches have been made in this way [1]-[3]. So far higher order matrix spectral problem and complex spectral problem are all attractive to the mathematical and physical science. However, due to theoretical difficulty and the complexity of computation, the relevant research is relatively rare for the present.
In this paper, we present a 3 × 3 AKNS matrix spectral problem
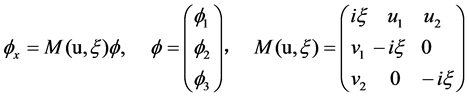 (1.1)
(1.1)
where the potential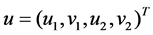 ,
, 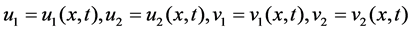 are complex-valued potential functions,
are complex-valued potential functions,  is a complex spectral parameter,
is a complex spectral parameter, . The relation between this 3rd-order complex
. The relation between this 3rd-order complex
spectral problem and the associated completely integrable system is considered. We derived the related evolution equation hierarchy, one of which is often referred to on the literature as the coupled nonlinear Schrödinger equation:
 (1.2)
(1.2)
which is used by Manakov for studying the propagation of the electric field in a waveguide [4]. Each equation governs the evolution of one of the components of the field transverse to the direction of propagation. Also it can be derived as a model for wave propagation under conditions similar to those where nonlinear Schrödinger equation applies and there are two wavetrains moving with nearly the same group velocity [5]. In recent years, this system is widely studied [6] [7] and used as a key model in the field of optical solitons in fibers [8] [9] to explain how the solitons waves transmit in optical fiber, what happens when the interaction among optical solitons influences directly the capacity and quality of communication and so on [10]-[12].
2. The Evolution Equations and Their Lax Pairs
Now, suppose  is the basic interval, if
is the basic interval, if  and their derivatives on x are all decay at infinity, then
and their derivatives on x are all decay at infinity, then ; if they are all periodic
; if they are all periodic 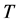 functions, then
functions, then . In order to get the evolution equations, we first solve the stationary zero-curvature equation:
. In order to get the evolution equations, we first solve the stationary zero-curvature equation:
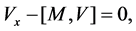 (2.1)
(2.1)
where
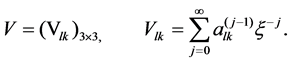 (2.2)
(2.2)
The auxiliary problem of the spectral problem is set as follows:
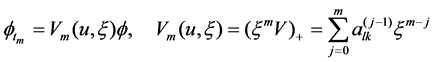 (2.3)
(2.3)
Let 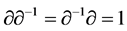 and the initial value
and the initial value
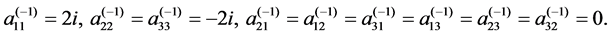 (2.4)
(2.4)
So the Lenard recursive sequence

is obtained and the Lenard recursive equation
![]() (2.5)
(2.5)
is given, where K and J are two bi-Hamiltonian operators [13]
![]()
![]()
![]()
![]()
![]()
and
![]()
The isospectral evolution equations are
![]() (2.6)
(2.6)
By (2.1)-(2.5), we have
Theorem 2.1.
![]()
is the Lax forms of evolution Equation (2.5). In other words, the hierarchy of solition Equation (2.5) is a isospectral compatible condition of (2.6).
Especially, if we take
![]() (2.7)
(2.7)
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
By (2.5),
![]()
![]()
if![]() , it is exactly the coupled nonlinear Schrödinger Equation (1.2) which is a well-known equation and is of great value in physics (where the symbol * denotes the complex conjugate).
, it is exactly the coupled nonlinear Schrödinger Equation (1.2) which is a well-known equation and is of great value in physics (where the symbol * denotes the complex conjugate).
3. A Finite-Dimensional Hamiltonian System
In order to give the constraints between the potential and the eigenfunction, First, the complex representation of the Poisson bracket is discussed.
The Poisson bracket of the real-valued function ![]() in the symplectic space
in the symplectic space ![]() is defined as follows:
is defined as follows:
![]()
The Poisson bracket of the complex-valued function F, H in the symplectic space ![]() is defined as follows:
is defined as follows:
![]()
Lemma 3.1. [15] Let
![]()
then the symplectic form ![]() can be written
can be written ![]() the complex Poisson bracket is equivalent to the real Poisson bracket when the Hamiltonian functions H and F are all real-valued functions, namely,
the complex Poisson bracket is equivalent to the real Poisson bracket when the Hamiltonian functions H and F are all real-valued functions, namely,
![]()
Especially, if![]() , the complex Hamiltonian canonical equation
, the complex Hamiltonian canonical equation
![]()
are equivalent to the real Hamiltonian canonical equation
![]()
Which plays an important role in the generation of the completely integrable system in the Liouville sense.
Consider the spectral problem (1.1) and it’s adjoint spectral problem
![]() (3.1)
(3.1)
A direct calculation shows that
![]()
where![]() . Then [14]
. Then [14]
![]() (3.2)
(3.2)
and
![]() (3.3)
(3.3)
Now, suppose ![]() is an eigenvalue of (1.1) and (3.1),
is an eigenvalue of (1.1) and (3.1), ![]() are the eigenfunctions for
are the eigenfunctions for![]() ,
,![]() . Then, the spectral problem (1.1) and it’s adjoint spectral problem (3.1) can be rewritten as follows:
. Then, the spectral problem (1.1) and it’s adjoint spectral problem (3.1) can be rewritten as follows:
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
Set![]() . We consider the following constraint:
. We consider the following constraint:
![]() (3.6)
(3.6)
Substituting (3.6) into (3.4), (3.5), we can get the
Hamiltonian function ![]()
![]() (3.7)
(3.7)
where
![]()
If the coordinates are as follows:
![]() (3.8)
(3.8)
The following theorem immediately holds.
Theorem 3.2. On the constraint (3.6), (3.4) and (3.5) with their conjugate representations are equal to the Hamiltonian canonical system
![]() (3.9)
(3.9)
Define the Hamiltonian function as follows:
![]() (3.10)
(3.10)
where
![]()
![]()
![]()
By (3.13)-(3.15), the following theorem hold.
Theorem 3.2. On the constraint (3.6), (3.4) and (3.5) with their conjugate representations are equal to the Hamiltonian canonical system
![]() (3.11)
(3.11)
Theorem 3.4. [16] [17] Suppose ![]() is an involutive solution of the Hamiltonian canonical equation systems (3.9) (3.11), then
is an involutive solution of the Hamiltonian canonical equation systems (3.9) (3.11), then
![]()
satisfies the evolution Equation (2.5).
Acknowledgements
This project is supported by the Doctoral Scientific Research Foundation of Shijiazhuang University (No. 11BJ009).