Effect of Hot Carrier on Amplitude Modulation and Demodulation of Gaussian High Power Helicon Wave in Homogeneous Longitudinally Magnetized Strain Dependent Dielectric Material ()
1. Introduction
A number of extensive researches have been carried out from the different researchers in worldwide to investigate the effect of modulation and demodulation of high power pump wave from nano-pulsed laser action. From this interaction of electromagnetic wave in solid-state plasmas, the numbers of application have been raised to diagnose the metals, semimetals and semiconductor [1] . Out of these materials, the number of collective modes arises in magnetized semiconductor plasma from nonlinear interaction at relatively large amplitude of the propagating pump wave. When an un-modulated electromagnetic wave starts to propagate through a semiconductor plasma or ionized gaseous plasma with periodically varying parameters, it gets modulated or demodulated amplitude or frequency. The modulation and demodulation of the pump wave can be considered with respect to either amplitude or in terms of frequency. The periodic variation in “z” and “t” dependent exponential parameter  may be induced by the propagation of the acoustic wave in semiconductor plasma, where m defines the modulation parameter. The periodic modulation caused by the time varying changes in carrier density and electron-electron collision frequency. This parameter arises from the periodic modulation of the magnetic field, power of the rf discharge or propagation of the acoustic wave inside the semiconducting material [2] . The frequency, intensity, and direction of optical beam are controlled from the scattering of light from sound or low frequency electromagnetic wave. In nonlinear acoustics an important field of study is amplification and frequency mixing of waves in semiconductors [3] . This method has been used for the design of acousto-optic modulators, based on the interaction of an acoustic wave or a low frequency wave with the incident laser beam. Various piezoelectric materials (like InSb, and high strain dielectric material such as BaTiO3) have been used to investigate the effect of modulation and demodulation of the plane wave in nonlinear dispersive medium by using the different approximation [4] . Lashmore-Davies [5] reported the mechanistic approaches for arising spontaneous beak up of a shear Alfven wave to study the modulation instability of finite amplitude.
may be induced by the propagation of the acoustic wave in semiconductor plasma, where m defines the modulation parameter. The periodic modulation caused by the time varying changes in carrier density and electron-electron collision frequency. This parameter arises from the periodic modulation of the magnetic field, power of the rf discharge or propagation of the acoustic wave inside the semiconducting material [2] . The frequency, intensity, and direction of optical beam are controlled from the scattering of light from sound or low frequency electromagnetic wave. In nonlinear acoustics an important field of study is amplification and frequency mixing of waves in semiconductors [3] . This method has been used for the design of acousto-optic modulators, based on the interaction of an acoustic wave or a low frequency wave with the incident laser beam. Various piezoelectric materials (like InSb, and high strain dielectric material such as BaTiO3) have been used to investigate the effect of modulation and demodulation of the plane wave in nonlinear dispersive medium by using the different approximation [4] . Lashmore-Davies [5] reported the mechanistic approaches for arising spontaneous beak up of a shear Alfven wave to study the modulation instability of finite amplitude.
Much more attention has been paid by the researcher to find out the basic problem of the frequency and amplitude modulation in the gaseous plasma. The charge carriers due to ionization of the gas, from the interaction of the high power laser wave, are responsible for arising the plasma in gaseous state. In most of study of modulation and demodulation, interaction with nonlocal effects such as diffusion of the charge exciting the change in responsible parameters such as nonlinear refractive index has been ignored during calculation. Nonlinear polarizations due to acousto-optic interaction in dielectric and semiconducting materials are playing an increasing role in optical modulation, demodulation and beam splitting [6] [7] . But in presence of electro-strictive effect, the nonlinearity is due to slow movement of free charge carrier from the diffusion effect which shows short distance travel before recombining. Hence, the charge carrier can be easily moved in nonlinear dispersive medium, particularly high mobility III-V type of semiconductor.
The charge carrier is easily excited in nonlinear dispersive media when an intense laser beam passes through it, and considerable heating raises the steady state temperature which is higher than that of lattice temperature. The carrier heating provides the momentum transfer collision frequency to an electron, thus modifying the mobility and diffusion of charge carriers, as well as conductivity of the dispersive medium by adsorption of ions from the gaseous state and hence it shows the refinement effect on modulation of amplitude or frequency. It is found that increasing the diffusion through charge carrier heating makes it more difficult to reflect or transmit the light from the local equilibrium which represents the unstable and stable TE and TM linear surface wave [8] . Ghosh and Rishi [9] at first time studied the diffusion induced modulation and demodulation of the acousto-optic frequency in magnetized semiconductor. The frequency modulated beam in less dispersive acoustic media is easily amplified due to excess charge carrier from enhanced diffusion. They reported the excitation of an acousto-helicon wave modulation of plasma wave in longitudinally (k, k0, k1 ‖ ‖ Bs) magnetized semiconducting plasma [10] . The scattering of the wave occurs from ordinary and the other extraordinary wave, and lies on the surface of a circular cone i.e.,  with a phase angle of
with a phase angle of . This imparts the effect of geometry of the dispersive media which supports the propagation of the helicon wave with the interaction from acoustic and transverse induced non-helicon wave through polarization. The considerable gain in frequency is obtained from the nonlinear interaction of pump-helicon wave
. This imparts the effect of geometry of the dispersive media which supports the propagation of the helicon wave with the interaction from acoustic and transverse induced non-helicon wave through polarization. The considerable gain in frequency is obtained from the nonlinear interaction of pump-helicon wave 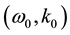 with a transversely acoustic wave
with a transversely acoustic wave 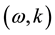 and another helicon wave
and another helicon wave 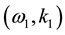 in cubic semiconductor plasma [11] .
in cubic semiconductor plasma [11] .
In this present article, our analysis can be employed to see the effect of hot carriers on the amplitude modulation instability of an intense helicon pump wave due to acoustic-optic interaction in diffusive strain dependent dielectric constant. The dispersion relation can be solved by considering the complex relation for diffusion dependent dispersion 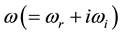 taking with the real and positive value of
taking with the real and positive value of  throughout the present analysis. The intense pump source interacts with semiconductor plasma generating the acoustic wave with the interaction from the diffusion of free carrier (through electron plasma wave) and acoustic phonons (through material vibration). The numerical analysis was made by selecting the different parameter of z and t and also assumed that the propagation of high power helicon wave inside the material followed the Gaussian profile. The propagation mode of high power helicon wave will be completely unstable; only when
throughout the present analysis. The intense pump source interacts with semiconductor plasma generating the acoustic wave with the interaction from the diffusion of free carrier (through electron plasma wave) and acoustic phonons (through material vibration). The numerical analysis was made by selecting the different parameter of z and t and also assumed that the propagation of high power helicon wave inside the material followed the Gaussian profile. The propagation mode of high power helicon wave will be completely unstable; only when 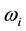 is less than
is less than ;
;  represents the growth-rate of unstable mode arising from the modulation and demodulation of the pump- wave. The interaction of free carrier and acoustic phonon induces a strong threshold electric field that modulates or demodulates the pump wave from unstable growth rate. Thus, the applied electric field generates the sinusoidal threshold electric field and acoustic wave in acousto-optic modulator which can enhance the hyperbolic growth rate for the amplitude modulation and demodulation of the acoustic wave frequency in diffusive strain dependent dielectric constant in presence of strong magnetic field and hot carrier.
represents the growth-rate of unstable mode arising from the modulation and demodulation of the pump- wave. The interaction of free carrier and acoustic phonon induces a strong threshold electric field that modulates or demodulates the pump wave from unstable growth rate. Thus, the applied electric field generates the sinusoidal threshold electric field and acoustic wave in acousto-optic modulator which can enhance the hyperbolic growth rate for the amplitude modulation and demodulation of the acoustic wave frequency in diffusive strain dependent dielectric constant in presence of strong magnetic field and hot carrier.
2. Dispersion Relation
The hydro-dynamical model is considered for the numerical calculation for the propagation of high power helicon pump wave in one-component homogeneous n-type piezoelectric semiconductor plasma of infinite extent with electrons as major charge carriers, along the direction z of externally applied static magnetic field, .
.
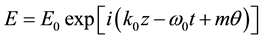 (1)
(1)
where,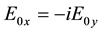 . The time harmonic Maxwell’s equation by assuming there is no external current, can be expressed as
. The time harmonic Maxwell’s equation by assuming there is no external current, can be expressed as![]() ,
, ![]() , where
, where![]() , where
, where ![]() is the equivalent dielectric. The magnetic field strength and plasma density gives the dependency of dispersion relation of the helicon wave. The well-known cold plasma dispersion tensor can be expressed by the following equation
is the equivalent dielectric. The magnetic field strength and plasma density gives the dependency of dispersion relation of the helicon wave. The well-known cold plasma dispersion tensor can be expressed by the following equation
![]() (2)
(2)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is the
is the
electron plasma frequency. By using analysis of Fourier analysis, the modified Maxwell’s equations for unbounded
plasma is given by![]() , where
, where![]() , is the index of refraction vector, whose direc-
, is the index of refraction vector, whose direc-
tion is the direction of the wave vector k and whose magnitude is the index of refraction. The basic equation involve in the analysis are the zeroth and first-order momentum transfer, Maxwell equation, continuity equation and the equation of motion of the lattice of a piezoelectric semiconductor. The classical equation of motion for carriers of charges e and effective mass m is
![]() (3)
(3)
![]() (4)
(4)
If we assume a constant drift velocity ![]() in the z-direction and let
in the z-direction and let ![]() and
and![]() .
.
Equation (3) yields
![]() (5)
(5)
Since the applied magnetic field B parallel to the![]() , and since the carriers are drifting, the time independent term are vanished. Helicon waves are basically low-frequency bounded whistler waves. In an ionosphere, whistler wave are right-hand-circularly polarized electromagnetic wave which are propagating along parallel to the magnetic field. The two normal are opposite in nature and travel with different phase velocity.
, and since the carriers are drifting, the time independent term are vanished. Helicon waves are basically low-frequency bounded whistler waves. In an ionosphere, whistler wave are right-hand-circularly polarized electromagnetic wave which are propagating along parallel to the magnetic field. The two normal are opposite in nature and travel with different phase velocity.
![]() (6)
(6)
In general, when high intensity wave interacts with semiconductor which contained high mobility charge, they gain momentum and energy as a result from electron collision. This collision develops the heat from momentum transfer (MTCF) through the relation
![]() (7)
(7)
The power absorbed per electron from the pump electric field becomes
![]() (8)
(8)
where * denotes the complex conjugate of the quantity and re denotes the real part. This power is dissipated in collision of electron from the acoustic phonon in the Brillouin active medium. Following Conwell [12] , the power dissipation per electron in collision with the polar optical phonon (POP) may be expressed as
![]() (9)
(9)
where![]() , in which
, in which ![]() is the energy of POP given by
is the energy of POP given by![]() , and
, and ![]() is the Debye
is the Debye
temperature of the medium. ![]() Is the field of POP scattering potential in which
Is the field of POP scattering potential in which ![]() and
and
![]() are the static and high-frequency dielectric permittivity of the medium, respectively.
are the static and high-frequency dielectric permittivity of the medium, respectively. ![]() Is the zeroth-order Bessel function of first kind. The Einstein equation is the basic relation between the ionic mobility µ
Is the zeroth-order Bessel function of first kind. The Einstein equation is the basic relation between the ionic mobility µ
to the ionic self-diffusion coefficient D (in cm2∙s−1)![]() . Therefore, for moderate heating of carrier, using
. Therefore, for moderate heating of carrier, using
(7) and (8), we obtain the expression for electron temperature and modified diffusion coefficient as
![]() (10)
(10)
![]() (11)
(11)
The equation of motion for an element of volume dxdydz and density ρ is
![]() (12)
(12)
The propagation of the acoustic wave (AW) in a crystal with SDDC is just possible by only longitudinal EKWs due to the piezoelectric effect, which is slightly induced by the transverse electric field of the helicon. By using the Poisson equation![]() , the piezoelectric field strength can be expressed by
, the piezoelectric field strength can be expressed by
![]() (13)
(13)
The piezo-electrically excited longitudinal plasma oscillation can be obtained from Equation (13) by considering (3) and (4)
![]() (14)
(14)
where![]() , N0 being the equilibrium electron concentration and n1 the electron concentration perturba-
, N0 being the equilibrium electron concentration and n1 the electron concentration perturba-
tion. Assuming that![]() , we get
, we get
![]() (15)
(15)
where![]() ,
, ![]() is the Debye screening length. Then the AW wave propagation may be written as
is the Debye screening length. Then the AW wave propagation may be written as
![]() (16)
(16)
If the AW frequency ![]() and
and![]() , then
, then![]() , where
, where ![]() -the Maxwell relaxation
-the Maxwell relaxation
frequency. The following procedure adopted by Ghosh and Agarwal [13] and using Equations (2) to (9) in collision dominated regime![]() ,
, ![]() , one obtain.
, one obtain.
![]() (17)
(17)
in which![]() ,
, ![]() and
and ![]() is the electron plasma frequency,
is the electron plasma frequency,
![]() the electron cyclotron frequency where
the electron cyclotron frequency where![]() .
. ![]() Is the electromag-
Is the electromag-
netic wave velocity in the crystal with lattice dielectric constant![]() ,
, ![]() is electron thermal velocity.
is electron thermal velocity.
As the density perturbation in the plasma has been assumed to vary as ![]()
![]() . Hence the initial helicon pump beam can now beat with these perturbations to produce forced wave disturbance at upper
. Hence the initial helicon pump beam can now beat with these perturbations to produce forced wave disturbance at upper ![]() and lower
and lower ![]() side-band frequencies. These side-bands are forced waves and one may write down the expression for them from Equation (10) as follows:
side-band frequencies. These side-bands are forced waves and one may write down the expression for them from Equation (10) as follows:
![]() (18)
(18)
in which ![]() traverse acoustic wave velocity in crystal,
traverse acoustic wave velocity in crystal, ![]() the frequency for
the frequency for
dispersive electron plasma wave and ![]() the dimensionless electromechanical coupling coeffi-
the dimensionless electromechanical coupling coeffi-
cient. Equations (9) and (4) one may write![]() , where
, where ![]() and
and ![]()
and the side band waves vary as![]() . The only nonlinear term present in Equation (13) is the one on the RHS and it is this term which couples the density variations at frequencies
. The only nonlinear term present in Equation (13) is the one on the RHS and it is this term which couples the density variations at frequencies ![]() back to the acoustic wave of frequency
back to the acoustic wave of frequency![]() .
.
![]() (19)
(19)
where![]() .
.
3. Growth Rate and Threshold Electric Field
In the slow wave limit, it is the quasi-static approx ![]() and obtain the dispersion relation in simplified
and obtain the dispersion relation in simplified
![]() (20)
(20)
From Equation (15) in absence of piezoelectric coupling coefficient ![]() one obtains
one obtains
![]() , (21)
, (21)
We assume ![]() and
and ![]() which is agreement with Steele and Vural [14] . Thus separating the real and imaginary part from Equation (5), we can obtain the expression at high magnetic fields from [1]
which is agreement with Steele and Vural [14] . Thus separating the real and imaginary part from Equation (5), we can obtain the expression at high magnetic fields from [1]
![]() (22)
(22)
and
![]() (23)
(23)
where![]() ,
, ![]() ,
, ![]() ,
, ![]()
Since ![]() the oscillatory electron fluid velocity is much larger than
the oscillatory electron fluid velocity is much larger than![]() , it always get
, it always get ![]() and consequently, H > 0. Hence above equation shows that the excited mode will be unstable only when
and consequently, H > 0. Hence above equation shows that the excited mode will be unstable only when ![]() and
and![]() . Now
. Now ![]() can be obtained
can be obtained
![]() (24)
(24)
In the presence of laser field one can obtain the threshold value of the electric field necessary for the onset instability by putting ![]() one can get
one can get
![]() (25)
(25)
So the threshold value of the electric field is obtain by [1]
![]() (26)
(26)
Above equation shows that for instability the condition ![]() must be satisfied. By adjusting the carrier concentration, we can easily find the suitable condition which satisfied for BaTiO3 high dielectric constant material. For a value of
must be satisfied. By adjusting the carrier concentration, we can easily find the suitable condition which satisfied for BaTiO3 high dielectric constant material. For a value of ![]() greater than
greater than ![]() we obtain the instability of the mode with a finite growth-rate given by utilizing above equations
we obtain the instability of the mode with a finite growth-rate given by utilizing above equations
![]() (27)
(27)
4. Results and Discussion
In this section, the numerical results of the possibility of modulation instability and the amplification of the acousto-helicon wave which arising from interaction of the pump helicon wave with acousto-helicon wave have been analyzed through Equations (28) and (29) for strain dependent dielectric material. The carrier heating on acousto-helicon interaction modifies the dependent parameter such as electron momentum transfer collision frequency (MTCF) (Equation (7)) and diffusion of charge carrier at the different temperature (Equation (10)) and hence consequently modifies the threshold electric field and modulation of a high power helicon wave effectively. The modulation instability and the amplification of acousto-helicon waves from Equations (26) and (27) was solved numerically as results from the transfer of modulation helicon wave to acousto-helicon wave for the different values of the semiconductor plasma parameters such as![]() ,
, ![]() , and
, and ![]() at the different temperature. As a typical case, the numerical calculation was performed for the BaTiO3 cubic crystals at 300K, with following typical constant are taken:
at the different temperature. As a typical case, the numerical calculation was performed for the BaTiO3 cubic crystals at 300K, with following typical constant are taken:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() . The crystal is subjected to irradiate with 10.6 μm nanosecond laser. The beauty of BaTiO3 is that its crystals structure is easily modified from the addition of impurities or creating the defect inside the lattice structure. Its easy tendency is due to formation of the solid solution with foreign atoms of the same size or fitted in the octahedral hole of the lattice arrangement. The electric field amplitude which is considered in the present investigation can be directly calculated from the pump intensity I0, expressed by the following expres-
. The crystal is subjected to irradiate with 10.6 μm nanosecond laser. The beauty of BaTiO3 is that its crystals structure is easily modified from the addition of impurities or creating the defect inside the lattice structure. Its easy tendency is due to formation of the solid solution with foreign atoms of the same size or fitted in the octahedral hole of the lattice arrangement. The electric field amplitude which is considered in the present investigation can be directly calculated from the pump intensity I0, expressed by the following expres-
sion:![]() .
.
Now let us consider the important case where the mechanistic approaches of spatial lattice formation is due to the diffusion process of photo-excited electrons or holes from the surface of semiconducting material by irradiation of the pump wave. The intensity distribution from the diffusion process between the threshold electric field can be expressed
![]() (28)
(28)
where ![]() is known as the diffusion field, T is the temperature, and e is the electronic charge. The
is known as the diffusion field, T is the temperature, and e is the electronic charge. The
fastest imaginable diffusion process from the charge carriers may be due to free flight of the particles between the different lattice site of stain dependent material with the upper limit D, which can be expressed by the diffu-
sion coefficient of an ideal gas![]() , where λ and
, where λ and ![]() are the mean free path and mean speed respective-
are the mean free path and mean speed respective-
ly. The thermo-dynamical equilibrium actually controlled the diffusion of the charge carriers by the jumping from one lattice position to other place by the interaction of acousto-helicon wave, then the residence time τ of
the particle on its site is given by![]() , where z define the coordination number indicating the number of
, where z define the coordination number indicating the number of
neighboring present sites. The hot carriers easily diffuse in entire lattice of BaTiO3. The random walk theory in a 3d can be considered for the self diffusion process and it is calculated from the following expression
![]() (29)
(29)
The entire diffusion process changes the modulation and amplification of the acousto-helicon wave which results from transfer of momentum and energy through pump wave. The numerical results are plotted in Figure 1 and Figure 2. The variation of threshold electric field dependent on interaction length and cyclotron frequency is depicted in Figure 1 and Figure 2 with including the carrier effect. The interaction length varies from 0 to 20 μm and the range of the cyclotron frequency is taken to be less than![]() . The produced threshold electric field varies sinusoidal with interaction length and cyclotron frequency. The threshold electric filed shows the maxima and minima with an increase the interaction length. It may be inferred from Figure 1 and Figure 2 that the amplitude modulation of the pump helicon in Figure 2 is found to be 100 times more than that from Figure 1. Due to diffusion of the charge carrier (CH), the surface nature of the threshold electric filed is not changed, but changed the magnitude only. The nature of variations of
. The produced threshold electric field varies sinusoidal with interaction length and cyclotron frequency. The threshold electric filed shows the maxima and minima with an increase the interaction length. It may be inferred from Figure 1 and Figure 2 that the amplitude modulation of the pump helicon in Figure 2 is found to be 100 times more than that from Figure 1. Due to diffusion of the charge carrier (CH), the surface nature of the threshold electric filed is not changed, but changed the magnitude only. The nature of variations of ![]() dependent on
dependent on ![]() with k+ are plotted in Figure 2 where Figure 2(a) shows the variation of
with k+ are plotted in Figure 2 where Figure 2(a) shows the variation of ![]() without CH and Figure 2(b) with diffusion of CH. Figure 2(a) indicates that the growth rate changes sharply with the increase in the cyclotron frequency
without CH and Figure 2(b) with diffusion of CH. Figure 2(a) indicates that the growth rate changes sharply with the increase in the cyclotron frequency![]() . The surface profile of the growth rate is not similar to surface profile of the threshold electric field. The surface of the electric field directly varies with
. The surface profile of the growth rate is not similar to surface profile of the threshold electric field. The surface of the electric field directly varies with![]() , whereas
, whereas ![]() have an inverse relation of
have an inverse relation of ![]() by assuming that there is no possibility of diffusion. Due to this relationship, they lose the sinusoidal nature of the propagation. Figure 2(b) presents the variation of the growth rate with diffusion of the carrier heating. There problem
by assuming that there is no possibility of diffusion. Due to this relationship, they lose the sinusoidal nature of the propagation. Figure 2(b) presents the variation of the growth rate with diffusion of the carrier heating. There problem
is solved by using Equation (28) after assuming that growth rate is directly proportional to![]() .
.
Figure 3 and Figure 4 shows the variation of the threshold electric filed and growth rate with the interaction length and cyclotron frequency which varies from 1 to 2.5 × 1014 Hz. These modulations tend to be minimum at![]() . On further increasing or decreasing the cyclotron frequency from the pump frequency
. On further increasing or decreasing the cyclotron frequency from the pump frequency![]() , they abruptly change the nature of propagation. The propagation of the threshold electric field below and greater than
, they abruptly change the nature of propagation. The propagation of the threshold electric field below and greater than ![]() is the inverse of each other. The profile shape is preserved in the propagation, although the width distribution changes with the magnetic field strength. Below and above cyclotron frequency from the pump frequency, only sign of the width is changed but nature of propagation is almost same.
is the inverse of each other. The profile shape is preserved in the propagation, although the width distribution changes with the magnetic field strength. Below and above cyclotron frequency from the pump frequency, only sign of the width is changed but nature of propagation is almost same.
![]()
![]() (a) (b)
(a) (b)
Figure 1. Variations of the amplitude modulation from the pump wave with interaction length and cyclotron frequency. Curve (a) without CH effect; (b) with CH effect.
![]()
![]() (a) (b)
(a) (b)
Figure 2. Dependence of growth rate from the pump wave with interaction length and cyclotron frequency. Curve (a) without CH effect; (b) with CH effect.
![]()
![]() (a) (b)
(a) (b)
Figure 3. Variations of the amplitude modulation from the pump wave with interaction length and cyclotron frequency![]() . Curve (a) without CH effect; (b) with CH effect.
. Curve (a) without CH effect; (b) with CH effect.
![]()
![]() (a) (b)
(a) (b)
Figure 4. Dependence of growth rate from the pump wave with interaction length and cyclotron frequency varies from![]() . Curve (a) without CH effect; (b) with CH effect.
. Curve (a) without CH effect; (b) with CH effect.
The growth rate having the same profile like threshold electric field but their variation is not uniform above and below the propagating plane. They show the slight variation in magnetite below and above the plane at![]() . The negative amplitude shows from the electron-electron collision and positive corresponding to the holes migration. This is due to shifting of one-quarter of the period of the lattice corresponding from the pump intensity distribution. The carrier heating effect shows the same profile with enhanced magnetite. These important studies of nonlinear interactions revels that the inclusion of heating effects modifies the mobility of the semiconducting materials by diffusion process. This can be explained by Equation (29); we can easily see that the partial modulation of the amplitude of the fundamental lattice vibration, corresponding to the parametric pair k and k+, is expressed by sum of the different phase based on the diffusion, as shown in Figure 4(a) and Figure 4(b).
. The negative amplitude shows from the electron-electron collision and positive corresponding to the holes migration. This is due to shifting of one-quarter of the period of the lattice corresponding from the pump intensity distribution. The carrier heating effect shows the same profile with enhanced magnetite. These important studies of nonlinear interactions revels that the inclusion of heating effects modifies the mobility of the semiconducting materials by diffusion process. This can be explained by Equation (29); we can easily see that the partial modulation of the amplitude of the fundamental lattice vibration, corresponding to the parametric pair k and k+, is expressed by sum of the different phase based on the diffusion, as shown in Figure 4(a) and Figure 4(b).
Pulse duration is important parameter to interact with the pump wave with semiconducting material. Not only change the interaction parameter, but also change the diffusion process of carrier heating by transferring the maximum amount of energy and momentum. This interaction changes the surface profile of modulation and amplification of the pump wave. The pulse duration modifies the carrier-lattice interaction by means of a collision time approximation. This effect is replaced ![]() to
to![]() , which not altered the resultant behavior of the surface profile of modulation and amplification of the pump wave. The carrier heating and its controlled is by the external electric field which give rise to the carrier drift velocity, directly related with the mobility of the diffusing species. Thus for analyzing the behavior of threshold electric field, Equation (29) are used to solve for the numerical results. Their effect is shown in Figure 5(a) and Figure 5(b); in this case, the cyclotron frequency is less than the pump frequency. In order to investigate the results, the pulse duration varies up to 25 ns. Their results are plotted in terms of
, which not altered the resultant behavior of the surface profile of modulation and amplification of the pump wave. The carrier heating and its controlled is by the external electric field which give rise to the carrier drift velocity, directly related with the mobility of the diffusing species. Thus for analyzing the behavior of threshold electric field, Equation (29) are used to solve for the numerical results. Their effect is shown in Figure 5(a) and Figure 5(b); in this case, the cyclotron frequency is less than the pump frequency. In order to investigate the results, the pulse duration varies up to 25 ns. Their results are plotted in terms of ![]() and pulse duration. Figure 5(a) shows the variation of the threshold electric field with pulse duration and cyclotron frequency, whereas the diffusion of the carrier heating enhances the magnitude of the amplitude modulation, as shown in Figure 5(b). The threshold electric field shows the sinusoidal nature of the propagation with small width and pulse height.
and pulse duration. Figure 5(a) shows the variation of the threshold electric field with pulse duration and cyclotron frequency, whereas the diffusion of the carrier heating enhances the magnitude of the amplitude modulation, as shown in Figure 5(b). The threshold electric field shows the sinusoidal nature of the propagation with small width and pulse height.
Similarly, Equation (29) is again solved for calculating the surface profile of threshold electric field for a BaTiO3 structure; in this case the profile is plotted from 1014 Hz to 2.5 × 1014 Hz. Figure 6(a) and Figure 6(b) show the propagation of threshold electric field with and without the presence of CH. The surface behavior is almost same but gives the entire profile of propagation. The carrier heating modifies the propagation of modulation
by introducing the diffusion related parameter ![]() and it is related to the number of collision events per
and it is related to the number of collision events per
cycle from electron-electron interaction, which changed the nature beyond the pump frequency![]() . In order to analyze growth rate in BaTiO3 with and without carrier heating (CH), Equation (29) are numerically used against the cyclotron frequency
. In order to analyze growth rate in BaTiO3 with and without carrier heating (CH), Equation (29) are numerically used against the cyclotron frequency ![]() and the pulse duration. During the investigation, the results of growth rate are again plotted below the pump frequency. Figure 7(a) and Figure 7(b) show the propagation of growth rate with pulse duration and cyclotron frequency up to 1.5 × 1014 Hz.
and the pulse duration. During the investigation, the results of growth rate are again plotted below the pump frequency. Figure 7(a) and Figure 7(b) show the propagation of growth rate with pulse duration and cyclotron frequency up to 1.5 × 1014 Hz.
![]()
![]() (a) (b)
(a) (b)
Figure 5. Dependence of growth rate from the pump wave with pulse duration and cyclotron frequency. Curve (a) without CH effect; (b) with CH effect.
![]()
![]() (a) (b)
(a) (b)
Figure 6. Variations of the amplitude modulation from the pump wave with interaction length and cyclotron frequency varies from![]() . Curve (a) without CH effect; (b) with CH effect.
. Curve (a) without CH effect; (b) with CH effect.
![]()
![]() (a) (b)
(a) (b)
Figure 7. Dependence of growth rate from the pump wave with pulse duration and cyclotron frequency. Curve (a) without CH effect; (b) with CH effect.
Similarly, Equation (29) is again presented graphically in Figure 8(a) and Figure 8(b) for a strain dependent dielectric with upper and lower sign of modulation; the presentations are made from 1014 Hz to 2.5 × 1014 Hz. During investigation, the results are found that the growth rate is non-uniform and non-sinusoidal with cyclotron frequency. Figure 8(a) shows a continuous and non-uniform growth-rate or a region of propagation with non-uniform pulse height from 1014 Hz to 2.5 × 1014 Hz, whereas Figure 8(b) shows a continuous and non- uniform growth-rate with large magnitude of non-uniform pulse height. The amplitude modulation and growth rate are enhanced 100 and 10 times by the diffusion of the CH. The profile shows only change in maxima and minima with pulse duration and cyclotron frequency. The curve has an oscillating character up and down with respect to zero planes which shows the pronounced conversion of the damping energy in different modes. The same observation has been observed for large pulsed duration as shown in Figure 9(a) and Figure 9(b). In this case, the duration of interaction varies up to 75 ns. Large numbers of pulse are generated during the propagation of high power pump wave with zero pulse width. The pulses are sinusoidal and the propagation is perfectly symmetrical. The carrier heating modifies the threshold amplitude modulation through diffusion as shown in Figure 9(a) and Figure 9(b). The pulse duration also modifies the growth rate by the transfer of momentum and energy with small pulse width or zero width. Figure 10(a) and Figure 10(b) show the growth rate with pulse duration and cyclotron frequency. The enhanced growth rates are observed in Figure 10(b) by the diffusion process from the carrier heating.
![]()
![]() (a) (b)
(a) (b)
Figure 8. Dependence of growth rate from the pump wave with interaction length and cyclotron frequency varies from![]() . Curve (a) without CH effect; (b) with CH effect.
. Curve (a) without CH effect; (b) with CH effect.
![]()
![]() (a) (b)
(a) (b)
Figure 9. Dependence of growth rate from the pump wave with pulse duration and cyclotron frequency. Curve (a) without CH effect; (b) with CH effect.
![]()
![]() (a) (b)
(a) (b)
Figure 10. Dependence of growth rate from the pump wave with interaction length and cyclotron frequency varies from![]() . Curve (a) without CH effect; (b) with CH effect.
. Curve (a) without CH effect; (b) with CH effect.
Below the pump frequency, the mass dependence threshold electric field controls the growth rate and the amplitude modulation. This figure illustrate the variation of growth rate with cyclotron frequency, which shows that growth rate with positive and negative are always in phase but it does not follows the sinusoidal nature: hence it shows the frequency and amplitude modulation from diffusion of hot carriers.
5. Conclusion
The results of this paper suggest that the modulation and growth rate of an electromagnetic wave can be easily achieved in many ferroelectric materials such as BaTiO3. The acousto-helicon is excited by the modulation of high power helicon pump wave in a longitudinally magnetized strain dependent dielectric material. The CH effect always increases the magnitude of the modulation and growth rate either interacting with change in interaction length (z) or oscillating the applied electric field by changing the pulse duration. The diffusion of carrier heating just modifies only the magnitude by retaining the shape of profile either in threshold electric field or growth rate. Hence, hot carriers are always much more favorable to modulate the pump wave via the interaction of acousto-helicon wave. This interaction parameter of the plasma media is very limited between the carriers heating and the lattice via diffusion process and is applied over a wide range of parametric wave number k or k+. The sinusoidal nature is found only in threshold electric field; meanwhile this nature is completely lost in growth rate of frequency and amplitude modulation. Non-uniform nature of growth rate is observed during the change in cyclotron frequency from 1014 Hz to 2.5 × 1014 Hz.
Acknowledgements
The authors are very much thankful to Principal Govt. M.V.M College for encouragement.