Convective Schrödinger Equation: Insights on the Potential Energy’s Role to Wave Particle Decay ()
1. Introduction
The conversion of electromagnetic energy to mass and vice versa is an old but still a very interesting problem to be studied in physics. One of the problems that still remain open is to explain in a more clear way the role of the potential energy on all those quantum wave-particle dissipation mechanisms addressed by quantum field theory―QFT/quantum mechanics. Here we study afresh this wave-particle dissipation problem using a simple alternative model, but considering the modification of the Schrödinger’s Equation due to the effect of the vacuum zero point energy due to vacuum electromagnetic fluctuations, as described by Bo Lehnert [1] .
2. Method
In order to study the quantum wave and particle Eigen modes excitation properties and the static potential role as a dissipation mechanism, we couple the Schrödinger’s wave equation, which models particles as waves, to the Maxwell’s wave equation for the electromagnetic field, since they are compatible mathematical structures. Here, we can view this alternative model as a plasma “wave-wave” interaction approach, where, instead of having only waves, we have particles and field interaction, using a linear wave model.
We start here with the non-relativistic Schrödinger’s equation, which is given by the expression below:
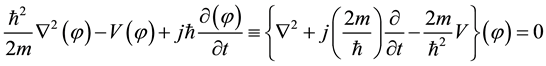 (1)
(1)
All the relevant terms present in Equation (1) are already defined in any basic quantum mechanics textbook ( ) [2] .
) [2] .
For the relativistic case, we have to use the Klein-Gordon equation given below:
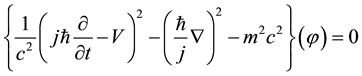
Expanding the squares:
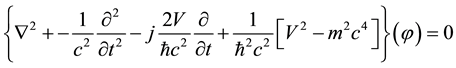 (2)
(2)
This equation is valid for zero spin particles, such as mesons, and photons with spin = 1.
The term 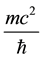 (=
(=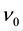 ) that can be obtained from Equation (2), should be considered as the particle intrinsic “Eigen frequency” (De Broglie frequency) via the dispersion relation:
) that can be obtained from Equation (2), should be considered as the particle intrinsic “Eigen frequency” (De Broglie frequency) via the dispersion relation:
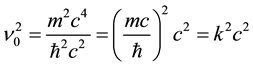 .
.
Now, we will derive a fundamental equation relating the energy of an impinging electromagnetic wave to particles mass, which are created at a transition region defined below.
Let us now split the interaction space in three relevant regions, described as follows [3] -[5] .
Region 1: Field region (Maxwell’s region).
Region 2: Transition region (fuzzy wave-particle region where Maxwell’s equation and Schrödinger’s equation couple).
Region 3: Particle region (Schrödinger’s region).
For the coupling to be consistent, we model the field region using the Klein-Gordon equation for non-massive photons,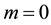 .
.
Then, we obtain
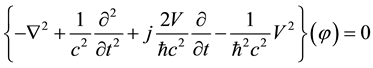 (3)
(3)
The basic equation at the transition region is obtained by coupling region 1 to region 2, which is done just using the “momentum conservation” condition:
 .
.
Therefore,
 (4)
(4)
Equation (4) is the basic equation to model the region―boundary layer―where particles and fields are not distinct―called here fuzzy region.
We have assumed that at the transition region a full energy and momentum conservation happens, so that the probability functions fully match.
To solve Equation (4), we consider the ansatz: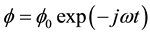 ; We can then find easily the two proper frequencies:
; We can then find easily the two proper frequencies:
 (5)
(5)
Equation (5) can be re-written as,
 (5’)
(5’)
The first root of (5’) just states that it is possible to convert mass into energy and vice-versa.
For zero external potential (V = 0), we get the “resonance” (photon-particle) conditions:
For plus sign, 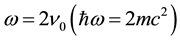 (two particles conversion) and for minus signω = 0, no conversion, the trivial solution is obtained.
(two particles conversion) and for minus signω = 0, no conversion, the trivial solution is obtained.
For non zero external potential, we can get another “resonance” (photon-particle) conditions:
If we consider the reflection of positively charged with spin = 0 particle from a barrier V, where this potential is zero to the left of the barrier and a constant V to the right, Equations (2) and (5) with m = 0 (massless boson) show that the mass of the particle to the right of the barrier V is 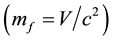 having a mode conversion in this case.
having a mode conversion in this case.
However, it is necessary with a “dissipation” mechanism, which in our case related to V (no V, no dissipation, no energy-mass conversion).
We will show now that the factor ![]() plays exactly the role of a “dissipation term”. It “permits” the va-
plays exactly the role of a “dissipation term”. It “permits” the va-
cuum to dissipate energy from photons. Where ![]() is the “natural” proper frequency, as stated above. Of course,
is the “natural” proper frequency, as stated above. Of course, ![]() must be fulfilled, in order to guarantee energy conservation.
must be fulfilled, in order to guarantee energy conservation.
This shows explicitly why the particle production must be in the presence of a potential V, it makes it possible, somehow, that fields could be dissipated into the form of matter.
This result also indicates that the energy conservation at the transition region (mode conversion region) “requests” that the photon energy is at least twice the created particle rest energy―a well known old result. To consider the spin dynamics it is necessary to use the Dirac’s relativistic quantum mechanics, but here we just want to see how V plays role in the field-mass conversion.
Now, for the sake of clarification, we will go further with the physical interpretation of the parameter ![]() and its role in quantum mechanics.
and its role in quantum mechanics.
In order to gain more insight on this dissipation mechanism, we go back once more to Equation (2), assuming![]() , we have the dispersion relation:
, we have the dispersion relation:
![]() .
.
We can rewrite this equation as,
![]()
Since
![]() ,
,
![]() , and
, and![]() .
.
Comparing now these results with the classical RLC circuit dispersion relation:
![]() ,
,
![]() ,
,
where L is the circuit inductance, C is the capacitance, and R the resistance.
Thus, the particle “natural” Eigen frequency can be written in this case as:
![]() .
.
Therefore, for a pumped “circuit”, the resonance condition is:
![]() , or
, or![]()
Here ω is the pumping (photon) energy/frequency.
The equivalent dissipation factor R/L for our case is![]() .
.
Concluding, we can consider the “mode conversion” regions as a resistance-impedance-capacitance-source circuit; the resonant region is driven by the impinging photons.
Also, due to the Equation (2), we have
![]() . (2’)
. (2’)
![]()
And finally (![]() ),
),
![]() ,
,
or
![]() .
.
This is the relation used for the total energy to model the motion of particles in a static external potential. So we have the two possible particle energy modes, V can be positive or negative. It is possible to have zero energy mode taking the plus sign and![]() , this shows how mass can become potential energy and vice-versa.
, this shows how mass can become potential energy and vice-versa.
Adding the momentum contribution into (2’), one gets,
![]() ,
,
So we get
![]()
or
![]()
For nonrelativistic particle conversion, the usual relation is,
![]()
For V = 0, we have the known conventional relation,
![]() .
.
L. Brillouin has also addressed the problem of relativity and potential energy using a different approach [6] . He considered an implicit mass content into the external potential energy.
Note that at high temperatures/energies T, it is possible to observe electron-positron and neutrino-antineutrino pairs, (i.e., T > 1 MeV) [7] [8] and so the Eigen mode model presented here makes full sense. The potential V may be just a few eV, but similar results can be obtained with a different formalism [9] .
3. Results
As a consequence of the above discussion, we will modify the original Schrödinger’s equation just adding a constructed potential operator in a way that this equation will have a convective term, and we will call this novel (modified) Schrödinger’s equation as Convective Schrödinger Equation.
By convective Schrödinger Equation, here, we just mean the conventional Schrödinger’s Equation where we introduce a term that is related to the vacuum zero point energy (relating it to the potential) [1] . In doing so, we get a modified Schrödinger Equation, where the potential energy is not anymore introduced in an ad hoc manner into this equation, but it is considered as an Hermitian operator, such as the total energy and the kinetic energy, and where the eigenvalues related to it are exactly the scalar potential. Therefore, the Schrödinger Equation is now only left with one ad hoc term―the particle mass―that might be further treated as an operator also, by say, using the Higgs’s Boson theory, for instance.
In order to move further with this study, it is important to say that both mass and potential, even if being observables quantities, are introduced ad hoc into Schrödinger’s equation and not postulated as Hermitian operators in the same way that the total energy and the kinetic energy are. That is, there are no formal Hermitian operators associated to those physical quantities, which would aloud to obtain real eigenvalues related to both, such as the ones we have for energy and momentum. This more realistic model would permit the access to the mass particle content creation from a more fundamental entity (complete Schrödinger’s function) and not just to access a probability density to find it, already massive, somewhere in a bounded or free state.
For the potential case, there are some discussions about its operator nature, but for mass this is still an open problem, in spite of Higgs’s explanation for particle mass origin via Higgs Boson.
We leave the mass operator problem for a future work and address afresh the problem of the operator nature of the potential and try to find an expression that could be useful to possibly model that. We saw above that the scalar potential could be understood as a dissipation “inducing” factor for wave―particle interaction as pair production, but now we move further to understand the operator nature of this physical quantity.
Therefore, the question to be answered now here is: Can the potential in Schroedinger’s equation be modeled as an Hermitian operator? If it is so, which form it would have? Can we get a measurable scalar potential as an eigenvalue of this operator? Has this question any physical meaning whatsoever?
There are people that consider the potential ![]() to be an operator just due to its modification of the original wave function
to be an operator just due to its modification of the original wave function ![]() via
via![]() . Therefore,
. Therefore, ![]() becomes
becomes ![]() via the “operation”
via the “operation”![]() . But is that so?
. But is that so?
There are also some/many other discussions about the operator nature of the potential, but we stop here, knowing that this is indeed a very interesting though controversy subject and therefore deserves further deeper discussion.
In order to proceed with this issue, let us consider Maxwell’s wave equation for pure field, but with dissipation:
![]() (6)
(6)
F is the wave field and s is the material conductivity.
By analogy, using the Klein-Gordon equation for massless photons, we have,
![]() (2’)
(2’)
Examining Equations (6) and (2’), we can identify the wave function dissipation factor for a photon in vacuum, but treated as particle. The factor “is”
![]() ,
,
Which means that particles wave function can grow in the presence of electrostatic potentials and photons. This phenomenon is related to the ZPE―Zero Point Energy [2] -[4] .
Therefore, the term ![]() plays the role of vacuum “energy to mass dissipation”, for photon. Where
plays the role of vacuum “energy to mass dissipation”, for photon. Where ![]() is the fine structure constant.
is the fine structure constant.
If V = 0, there is no dissipation.
It is interesting to mention that if we consider the potential V as an observable, not included ad hoc at the Schrödinger’s equation, as it is in the conventional quantum mechanics, a “potential operator” could be understood as:
![]() .
.
The important point is now to known the physical meaning of the operator![]() .
.
We consider at this point the “convection” displacement current (using a revised electromagnetic theory), that is valid for a point charged particle, which moves with velocity v. The “operator condutivity” can be writen as [3] [4] :
![]() .
.
Therefore, it might well be that the operator potential could be written as:
![]() (7)
(7)
The second term in (7) is related to the vacuum longitudinal Eigen modes. They do not appears (exist) in the conventional Maxwell’s electromagnetic theory. This factor is considered a convection term related to a convection displacement current, as already mentioned it describes the contribution to the displacement current of a single point-shaped charged particle moving with velocity v [3] -[5] .
We apply now this operator (7) on the particle standing wave function,
![]() ,
,
The above solution![]() , with
, with ![]() obtained satisfying the boundary conditions, describes standing waves of the time-dependent equation, which are the states with definite energy, those standing waves are called energy (“frequency”) Eigen state.
obtained satisfying the boundary conditions, describes standing waves of the time-dependent equation, which are the states with definite energy, those standing waves are called energy (“frequency”) Eigen state.
We have then, of course, for a particle (electron for instance) in the presence of a potential V.
![]() (7’)
(7’)
Considering here the wave function of a free particle, but under the influence of a potential V, we have:
![]() .
.
The potential “double-eigenvalue” is obtained via,
![]()
Thus:![]() .
.
It means that E is the total energy eigenvalue via the time operator and ![]() is the kinetic energy eigenvalue via the convection term. So, V is type “bilinear” operator.
is the kinetic energy eigenvalue via the convection term. So, V is type “bilinear” operator.
So, from (7’), we can write a new type of Schrödinger’s equation, “convection” Schrödinger equation―which contains in its structure the energy equipartion (factor 1/2) for particle and anti-particle:
![]() .
.
Now, we get a real formal “full” energy operator Schrödinger’s equation, self-consistently: E = T + V e V = E − T, eigenvalues of ![]() and
and![]() .
.
4. Conclusions
The results presented in this paper show that the potential, combined with the magnetic permeability/electric permittivity (implicit vacuum entities) and the Planck’s constant, plays the role of dissipation factor for the conversion of electromagnetic fields to particles and vice-versa.
Also, considering the contribution of the time convective derivative term (convective displacement current) [3] [4] , for a motion particle, we have derived a novel modified Schrödinger’s equation, which we have called here the “Convective” Schrödinger Equation. This equation takes into consideration, in a formal way, the potential as an operator related to the observable potential energy, and not adding it in a ad hoc manner as done in the usual Schrödinger’s Equation.
In the past, the study of relativistic particles has been in the exclusive domain of high-energy and particle physics. In grapheme theory, nonetheless, the linear electronic band dispersion near the Dirac points gave rise to charge carriers (electrons or holes) that propagate as if they were massless fermions with speeds of the order of 106 m/s rather than the speed of light. Hence, charge carriers in this structure had to be described by the massless Dirac equation or the Schrödinger’s equation when the compaction of graphene device generates mass proportional to conductivity. The physics of relativistic electrons is thus now experimentally accessible in graphene based solid-state devices, whose behavior differs drastically from that of similar devices fabricated with usual semiconductors. Consequently, new unexpected phenomena have been observed while other phenomena that were well-understood in common semiconductors such as the quantum Hall effect and weak-localization, exhibited surprising behavior in graphene. Thus, the graphene devices enabled the study of relativistic dynamics in controllable nano-electronic circuits (relativistic electrons on-a-chip). The Convective Schrödinger Equation (convection displacement current) allows basic understanding of electronic processes in graphene devices, which have conductivity in presence of electromagnetic fields (see Equations (10)-(12) of ref. [8] ). It also allowed for the observation of some subtle effects, previously accessible only to high-energy physics, such as Klein tunneling and vacuum breakdown [10] -[12] .
A further and deeper discussion on novel insights of field, matter (particles and anti-particles) and vacuum dynamics can be found in references [1] [3] -[5] .
Acknowledgements
The authors would like to thank Bo Lehnert for general discussions and suggestions considered in this work.