Generalized Algorithms of Discrete Optimization and Their Power Engineering Applications ()
1. Introduction
Discrete, integer, and Boolean (in the general case, discrete) optimization problems have important applications in many fields [1] [2] . Taking this into account, it should be stressed that direct determination of discrete solutions to problems of discrete character is necessary. This is associated with the fact that even though at the cost of ignoring discreteness of parameters, with smoothing of functions, it is possible to replace an actual objective function by a convex or concave function defined on a convex region, with such an approach the danger exists that the objective function will be distorted (with a deviation from the optimum) or that the constraints will be violated (see a simple example in Section 3). Moreover, the transition from the discrete model to its convex analog can lead to considerable “coarsening” the model that often makes vapid its essence [3] . Finally, with orientation to discrete methods it is possible to pose and solve problems of combinatorial nature, which have previously not been considered [3] .
Theoretical and experimental evaluations, discussed in [4] [5] , for example, have revealed significant drawbacks of exact methods of discrete programming. Besides, estimates of computational complexity [6] in solving discrete problems indicate that their NP-completeness does not permit one to develop general methods with a polynomial dependence on the problem dimension [7] . Thus, the development and application of approximate methods are the main direction in the evolution of discrete programming.
The algorithms discussed in the present paper are based on a combination of formal (the method of normalized functions [8] ) and heuristic (elements of the greedy heuristics [9] -[11] , generally, providing the best heuristic among possible heuristics with a priori estimates) procedures. The algorithms permit one to obtain quasi- optimal solutions after a small number of steps, overcoming the problem NP-completeness. They do not require an analytical specification of objective functions and constraints, ensuring the flexibility and the possibility to solve problems, for which adequate analytical descriptions are difficult or impossible.
In the process of formulating and solving a wide range of problems related to the design, planning, operation, and control of complex systems, one inevitably encounters different types of uncertainty [12] -[14] . Considering this, it should be stressed that taking into account the uncertainty factor in shaping mathematical models is to be inherent to the practice of systems analysis. This serves as a means for increasing the adequacy of the built models and, as a consequence, the credibility and factual effectiveness of solutions based on their analysis.
Investigations of recent years show the benefits of applying fuzzy set theory [15] to deal with various types of uncertainty. Its use in problems of optimization character offers advantages of both fundamental nature (the possibility of obtaining more effective, less “cautious” solutions) and computational character [16] [17] . Considering this, the present paper also reflects results related to modifying the generalized algorithms to solve discrete problems with fuzzy coefficients in objective functions and constraints as well as multiobjective discrete problems.
2. Problem Formulation
From the diversity of discrete optimization problems it is possible to distinguish two comprehensive classes. The first class is associated with the general problem of discrete programming, including integer, Boolean, and discrete programming problems proper. The problems with discrete variables may be reduced to integer or, in the general case, to Boolean models [1] [18] . However, such a reduction, usually, substantially, increases the problem dimensionality [3] .
The second class of models is related to the problems of combinatorial type. In their solution, an extremum of the objective function is defined on a given finite discrete set A. The totality of objects obtained from A (for example, combinations or permutations) as well as objects obtained as a result of executing logical operations on elements of A [3] may be considered as a combinatorial space D. The problem is formulated as a search for
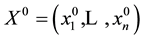 from
from  providing an extremum of the objective function, i.e.,
providing an extremum of the objective function, i.e., .
.
The combinatorial problems are the most difficult from the computational viewpoint. Their solution is based, in the main, on finiteness of  and the problem specificity. Many combinatorial problems may be reduced to problems of integer or Boolean programming. For instance, Ibaraki [19] defines sufficient conditions of reducibility of combinatorial problems to integer programming models but shows that there is no a general algorithm for such reducibility, even it is realizable. Besides, in many cases reducibility is reached by accepting considerable assumptions, sharp increasing model dimension, and losing the possibility to effectively exploit combinatorial properties of the initial problem [3] .
and the problem specificity. Many combinatorial problems may be reduced to problems of integer or Boolean programming. For instance, Ibaraki [19] defines sufficient conditions of reducibility of combinatorial problems to integer programming models but shows that there is no a general algorithm for such reducibility, even it is realizable. Besides, in many cases reducibility is reached by accepting considerable assumptions, sharp increasing model dimension, and losing the possibility to effectively exploit combinatorial properties of the initial problem [3] .
In this connection, when solving discrete problems, it is important that their formulation and solution should exploit those properties and peculiarities of the problems, which promote their effective solution. Considering this, the desirability of allowing for constraints on the discreteness of in the form of discrete sequences
 (1)
(1)
has been validated in [18] ; here 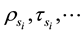 are technical, economic, etc. characteristics required for forming objective functions, constraints, and their increments, which correspond to the sth discrete (integer, Boolean) value of the variable
are technical, economic, etc. characteristics required for forming objective functions, constraints, and their increments, which correspond to the sth discrete (integer, Boolean) value of the variable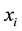 . Considering this, a maximization problem may be formulated as follows.
. Considering this, a maximization problem may be formulated as follows.
Assume we are given discrete sequences of the type (1) (increasing or decreasing, depending on the problem formulation). From them it is necessary to choose parameters that the objective
 (2)
(2)
is met while satisfying
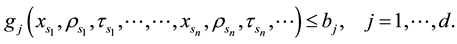 (3)
(3)
The objective function (2) is interpreted as concave and the constraints (3) are interpreted as convex.
Given the maximization problem (1)-(3), one can formulate a minimization problem. In particular, from the discrete sequences of the type (1) it is necessary to choose parameters that the objective
 (4)
(4)
is met while satisfying
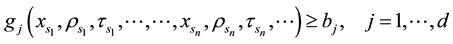 . (5)
. (5)
The objective function (4) is interpreted as convex and the constraints (5) are interpreted as concave.
3. Solution Algorithms
Let us consider the Boolean problem of maximization of
 , (6)
, (6)
while satisfying
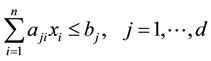 , (7)
, (7)
where ,
,  ,
,  ,
, ![]() ,
, ![]() , and
, and ![]()
![]() .
.
The idea of one of popular methods, associated with the class of heuristic methods, may be illustrated by analyzing (6) and (7) for ![]() (the 0 - 1 knapsack problem). It is possible to assume that
(the 0 - 1 knapsack problem). It is possible to assume that![]() ,
, ![]() are arranged as
are arranged as
![]() . (8)
. (8)
It allows one to try to maximize (6) on the basis of the largest![]() , considering
, considering![]() , then
, then![]() , and so on until (7) is observed. Similar methods are called greedy methods. Regardless of their “naivety”, in many cases, as it was indicated above, they represent the best heuristic among other heuristics with a priory estimates. However, a specter of problems is not restricted by the case of d = 1. Taking this into account, we discuss below ways of constructing algorithms for the general case (d > 1) to solve problems (linear as well as nonlinear), which can include not only Boolean, but also integer and discrete variables.
, and so on until (7) is observed. Similar methods are called greedy methods. Regardless of their “naivety”, in many cases, as it was indicated above, they represent the best heuristic among other heuristics with a priory estimates. However, a specter of problems is not restricted by the case of d = 1. Taking this into account, we discuss below ways of constructing algorithms for the general case (d > 1) to solve problems (linear as well as nonlinear), which can include not only Boolean, but also integer and discrete variables.
When analyzing (6) and (7) for d = 1, the maximization is reached by expending only one type of resources. If d > 1, the optimization process is stopped when a remaining amount of only one of resources is not sufficient for next incrementing any of xi,![]() . Thus, we can speak about “equivalence” of different types of resources from the point of view of terminating the process of maximizing (6). Therefore, it is advisable to have a single measure for different resources. This leads to the idea of normalization [8] . For example, the constraints (7) are reduced to a single arbitrary resource b as
. Thus, we can speak about “equivalence” of different types of resources from the point of view of terminating the process of maximizing (6). Therefore, it is advisable to have a single measure for different resources. This leads to the idea of normalization [8] . For example, the constraints (7) are reduced to a single arbitrary resource b as
![]() , (9)
, (9)
where t is the optimization step number.
Applying (9), it is possible to transform the constraints (7) to equal conditions. For instance, before the first optimization step we have
![]() . (10)
. (10)
Assume that at step t, variable ![]() is at its discrete level
is at its discrete level ![]() and its associated parameters
and its associated parameters ![]() are at
are at
the respective levels![]() . These can be gathered in what we introduce as the set
. These can be gathered in what we introduce as the set![]() .
.
Then the algorithm of solving the maximization problem (1)-(3), taking into account the results of [3] [20] , can be written in the following form.
1) The components of the vector ![]() are evaluated as follows:
are evaluated as follows:
![]() , (11)
, (11)
where ![]() is the set of variables at the tth step which, at their present values satisfy all constraints (3). In (11),
is the set of variables at the tth step which, at their present values satisfy all constraints (3). In (11), ![]() is the increment in the jth constraint when
is the increment in the jth constraint when ![]() undergoes a step change from its level
undergoes a step change from its level ![]() to the next level
to the next level ![]() while all the other
while all the other![]() ,
, ![]() remain at their current levels
remain at their current levels![]() :
:
![]() . (12)
. (12)
For t = 1 we have ![]() (
(![]() is the initial set of variables) and
is the initial set of variables) and![]() .
.
2) If![]() , then go operation 3, otherwise the calculations are completed because the solution is obtained.
, then go operation 3, otherwise the calculations are completed because the solution is obtained.
3) The components of the vector ![]() are calculated as follows:
are calculated as follows:
![]() (13)
(13)
4) If![]() , then go to operation 5, otherwise the calculations are completed because the solution is obtained.
, then go to operation 5, otherwise the calculations are completed because the solution is obtained.
5) The components of the vector ![]() are calculated as:
are calculated as:
![]() . (14)
. (14)
6) The index ![]() of the variable to be incremented is determined from the following condition:
of the variable to be incremented is determined from the following condition:
![]() . (15)
. (15)
7) We recalculate the current values of the following quantities:
![]() (16)
(16)
![]() . (17)
. (17)
8) If![]() , then go to operation 1, taking t = t + 1; otherwise the calculations are completed because the solution is obtained.
, then go to operation 1, taking t = t + 1; otherwise the calculations are completed because the solution is obtained.
Commenting the algorithm of solving the maximization problem (1)-(3), it is necessary to indicate that the execution of its operation 1 provides determination of the constraint with the most scarce type of the resource![]() ,
, ![]() for every variable at the given step. In essence, the execution of (11) permits one to construct
for every variable at the given step. In essence, the execution of (11) permits one to construct
a convolution:![]() . Therefore, at each optimization step we obtain an increment of that
. Therefore, at each optimization step we obtain an increment of that ![]() th variable
th variable
which maximizes the increment of the objective function per unit normalized resource b. In this connection, the utilization of (14) and (15) is similar to (8). Besides, the execution of operations 2 and 4 is directed at excluding variables that lead to violation of the constraints (3) or to decreasing the objective function of (2).
The problem of minimization (1), (4), and (5) is more difficult than the problem (1)-(3). In particular, in the case of maximization we stop changing the variable xi when at least one of the constraints (3) is violated. At the same time, in the minimization process the optimization is completed on any variable when all constraints (5) are obeyed. Therefore, there is in the case of maximization usually only one “deficient” constraint at each step requiring attention. At the same time, in minimization we have to pay attention to each constraint because the optimization process cannot be completed until all constraints (5) have been obeyed.
It is assumed that the initial constraints (5) are already normalized and are presented in the following form:
![]() . (18)
. (18)
The algorithm of solving the minimization problem (1), (4), and (5), using the results of [3] [20] , can be presented in the following form.
1) The components of the vector ![]() are evaluated as follows:
are evaluated as follows:
![]() . (19)
. (19)
In (19),
![]() , (20)
, (20)
where ![]() is the set of the constraints (5) at the tth step. For t = 1 we have
is the set of the constraints (5) at the tth step. For t = 1 we have ![]() (
(![]() is the initial set of constraints);
is the initial set of constraints);![]() .
.
2) The components of the vector![]() ,
, ![]() are calculated in accordance with (13).
are calculated in accordance with (13).
3) The components of the vector![]() ,
, ![]() are calculated on the basis of (14).
are calculated on the basis of (14).
4) The index ![]() of the variable to be incremented is determined from the following condition:
of the variable to be incremented is determined from the following condition:
![]() . (21)
. (21)
5) We recalculate the current values of the quantities![]() ,
, ![]() , using (16), and
, using (16), and
![]() . (22)
. (22)
6) If![]() , then go to operation 7; otherwise the calculations are completed because the solution is obtained.
, then go to operation 7; otherwise the calculations are completed because the solution is obtained.
7) If![]() , then go to operation 1, taking t = t + 1; otherwise the calculations are completed because the problem has no solution.
, then go to operation 1, taking t = t + 1; otherwise the calculations are completed because the problem has no solution.
Commenting the algorithm of solving the minimization problem (1), (4), and (5), it is necessary to indicate that the execution of its operation 1 provides the convolution of the set of constraints (5) at the given optimization step. In this connection, at each step of optimization we obtain an increment of that ![]() th variable which minimizes the increment of the objective function per unit total expenditure of normalized resources. The execution of operation 6 is associated with excluding such constraints (5) which are already satisfied. The algorithm has no operation similar to operation 4 of the algorithm of solving the maximization problem. This does not restrict a range of its applications because prior to using the algorithm it is possible to carry out minimization of the objective function (4) without considering the constraints (5).
th variable which minimizes the increment of the objective function per unit total expenditure of normalized resources. The execution of operation 6 is associated with excluding such constraints (5) which are already satisfied. The algorithm has no operation similar to operation 4 of the algorithm of solving the maximization problem. This does not restrict a range of its applications because prior to using the algorithm it is possible to carry out minimization of the objective function (4) without considering the constraints (5).
Numerous comparisons of solutions for diverse types of problems given, for instance, in [1] [21] , based on applying the algorithms presented above (with the upper bounds of the number of operations ![]()
for Boolean and ![]() for integer and discrete linear problems) and exact methods, show
for integer and discrete linear problems) and exact methods, show
their convincing agreement. This is also confirmed by numerous results on “good” behavior of the greedy algorithms [22] for wide classes of discrete optimization problems. However, the authors of [23] indicate that the greedy algorithms are to be used with caution. Taking into account these opinions, it is rational to have not only one, but several algorithms realizing different strategies. Considering this, so-called “duplicate” algorithms have been elaborated on the basis of a qualitative analysis of the problem statement. In particular, one of the “duplicate” algorithms is based on evaluating the components of the vector ![]() (operation 1 of the algorithm of solving the minimization problem) as follows:
(operation 1 of the algorithm of solving the minimization problem) as follows:
![]() , (23)
, (23)
where![]() ,
, ![]() ,
, ![]() are calculated on the basis of (12).
are calculated on the basis of (12).
The utilization of the “duplicate” algorithms can be considered, in a certain measure, as a guarantee of obtaining optimal solutions. Furthermore, the analysis of one and the same problem on the basis of several algorithms allows obtaining a series of solutions of equal worth, which is important as well.
As an example of the use of the “duplicate” algorithm associated with applying (23) we consider a problem of selecting locations and sizes of capacitors for a distribution network whose scheme and parameters are shown in Figure 1. It also gives the loads of transformers as well as load flow. For simplicity, the problem is solved under a simplified statement directed at minimizing a total installed power of low voltage capacitors while the constraints on lower voltage limits for maximal load levels are satisfied.
The discrete sequence of low voltage capacitor sizes is the following:
![]() (24)
(24)
It is necessary to select sizes of capacitors which minimize the objective function
![]() (25)
(25)
![]()
Figure 1. Network scheme, its parameters, and loads.
while satisfying the following constraints on lower voltage limits:
![]() (26)
(26)
The solution of (24)-(26), based on applying of the “duplicate” algorithm associated with the use of (23), is the following: ![]()
![]()
![]()
![]() and
and ![]()
![]() The corresponding value of the objective function (25) is F = 312 kVAr.
The corresponding value of the objective function (25) is F = 312 kVAr.
The solution of the problem (25) and (26) with ignoring the constraints (24) on variable discreteness, based on applying the simplex method of linear programming, is the following: x1 = 0 kVAr, x2 = 34 kVAr, x3 = 104 kVAr, x4 = 12 kVAr and x5 = 54 kVAr. Rounding the obtained values to the nearest discrete ones does not permit one to obtain a feasible solution. Rounding the obtained values to the nearest higher discrete ones provides the following solution: x1 = 0 kVAr, x2 = 78 kVAr, x3 = 156 kVAr, x4 = 78 kVAr and x5 = 78 kVAr. The corresponding value of the objective function (25) is F = 390 kVAr.
Another “duplicate” algorithm is associated with the results of [9] and is based on calculating![]() ,
, ![]() ,
, ![]() in the following form:
in the following form:
![]() (27)
(27)
with recalculating![]() ,
, ![]() (operation 5 of the algorithm of solving the minimization problem) as
(operation 5 of the algorithm of solving the minimization problem) as
![]() . (28)
. (28)
As an additional means for possible improving the efficiency of solutions may serve the formulation and analysis of one and the same problem within the framework of mutually interrelated models (1)-(3) and (1), (4), and (5). Applying this approach, if we have the increasing (decreasing) sequences (1) for the problem (1)-(3), the sequences (1) are to be decreasing (increasing) for the problem (1), (4), and (5). Thus, it is possible to solve one and the same problem “from above” as well as “from below” as well. This approach is fruitful and also serves for solving problems with fuzzy coefficients discussed below.
The described results have a high degree of generality and have been used in solving diverse power engineering problems discussed below.
4. Problems with Fuzzy Coefficients
Although there are diverse formulations of optimization problems with fuzziness (for instance, [15] [24] [25] , in opinion of the authors of [15] [24] , the problems with fuzzy coefficients in objective functions and constraints are to be considered as a general class of fuzzy mathematical programming problems.
Generalizing (1)-(3), it is possible to construct the problem of choosing parameters from discrete sequences of the type (1) that the objective
![]() (29)
(29)
is met while satisfying
![]() . (30)
. (30)
The objective function of (29) and constraint (30) include fuzzy coefficients, as indicated by the ~ symbol.
Generalizing (1), (4), and (5), it is possible to construct the problem of choosing parameters from discrete sequence of the type (1) that the objective
![]() (31)
(31)
is met while satisfying (30).
The models (1), (29), and (30) and (1), (31), and (30) generalize the models analyzed, for instance, in [26] [27] whose formulation with deterministic information have been considered in [3] [18] .
An approach [17] [28] to handling the constraints such as (30) involves replacing each of them by a finite set of nonfuzzy (deterministic) constraints, represented in the form of inequalities. Depending on the essence of the problem, it is possible to change from the problem (1), (29), and (30) or (1), (31), and (30) to the problem (1), (29), and (3) or (1), (31), and (5) with fuzzy coefficients in the objective functions alone. The solution of the problem (1), (29), and (3) is possible on the basis of modifying the algorithm of solving the maximization problem (1)-(3). The solution of the problem (1), (31), and (5) is associated with modifying the algorithm of solving the minimization problem (1), (4), and (5) or the corresponding “duplicate” algorithms. In particular, the execution of algebraic operations on fuzzy numbers by means of the expressions (13) and (14) is accomplished on the basis of the results of [29] .
To compare alternatives in accordance with (15) or (21) it is necessary to use the corresponding methods, considered, for instance, in [30] -[32] . Chen and Hwang [30] classify four groups of methods related to the ordering of fuzzy quantities. Among these groups, the authors of [33] consider the construction of fuzzy preference relations for pairwise comparisons as the most practical and justified way. Considering this, it is necessary to distinguish the fuzzy number ranking index introduced by Orlovsky [24] based on the conception of a membership function of a generalized preference relation.
If ![]() and
and ![]() have the membership functions
have the membership functions ![]() and
and![]() , then quantity
, then quantity
![]() (32)
(32)
is the degree of preference![]() , while
, while
![]() (33)
(33)
is the degree of preference![]() . These agree with several important fuzzy number ranking indices [17] . Examples of the application of the dependencies (32) and (33) are given in [17] . However, our experience shows that in many cases the membership functions of the alternatives
. These agree with several important fuzzy number ranking indices [17] . Examples of the application of the dependencies (32) and (33) are given in [17] . However, our experience shows that in many cases the membership functions of the alternatives ![]() and
and ![]() compared form flat apices (for example, [17] ), i.e., they are so-called flat or trapezoidal fuzzy numbers [15] . In view of this, when using (32) and (30), it may happen that
compared form flat apices (for example, [17] ), i.e., they are so-called flat or trapezoidal fuzzy numbers [15] . In view of this, when using (32) and (30), it may happen that ![]() and
and ![]() are indistinguishable if
are indistinguishable if![]() . In such situations the modified algorithms of discrete optimization do not allow one to obtain unique solutions: they “stop”. This occurs also with other modifications of traditional mathematical programming methods (this is illustrated in [28] [34] by simple examples) because a combination of the uncertainty and the relative stability of optimal solutions produces so-called decision uncertainty regions. In this connection, other indices may be used as additional means for the ranking of fuzzy numbers.
. In such situations the modified algorithms of discrete optimization do not allow one to obtain unique solutions: they “stop”. This occurs also with other modifications of traditional mathematical programming methods (this is illustrated in [28] [34] by simple examples) because a combination of the uncertainty and the relative stability of optimal solutions produces so-called decision uncertainty regions. In this connection, other indices may be used as additional means for the ranking of fuzzy numbers.
The review of techniques which have been developed for ranking of fuzzy numbers can be found in [32] . This study covers the analysis of the fuzzy ranking indices proposed before 1998 (among more recent works in this field, it is possible to distinguish, for instance, [35] [36] ).
The authors of [32] count more than 35 existing fuzzy number ranking indices, indicating that unlike in the case of real numbers, fuzzy quantities have no natural order. The idea with the ordering of fuzzy quantities is to convert a fuzzy quantity into a real number and base the comparison of fuzzy quantities on these real numbers. Each conversion way pays attention to a special aspect of fuzzy quantity. As a consequence, each approach suffers from some defects if only one real number is associated with each fuzzy quantity. Cheng [37] also indicates that many of indices produce different rankings for the same problem. The authors of [28] [31] [37] underline that fuzzy number ranking indices occasionally result in choices which appear inconsistent with intuition. Finally, the majority of indices for the ranking of fuzzy quantities have been proposed with the aspiration for obligatory distinguishing the alternatives. This is not natural because the uncertainty of information creates the decision uncertainty regions [17] .
There is another approach that is better validated and natural for the practice of decision making. It is associated with the transition to multiattribute choosing alternatives in a fuzzy environment because the application of additional criteria (including the criteria of qualitative character, such as “investment attractiveness”, “flexibility of development”, etc.) can serve as a convincing means to contract the decision uncertainty regions.
Before starting to discuss questions of multiattribute decision making in a fuzzy environment, it is necessary to note that considerable contraction of the decision uncertainty regions may be obtained by formulating and solving one and the same problem within the framework of mutually interrelated models:
1) model of maximization (29) with the constraints (30) approximated by (3);
2) model of minimization (31) with the constraints (30) approximated by (5).
When using this approach, solutions dominated by the initial objective function are cut off from above as well as from below to the greatest degree [28] . It should be stressed that this approach is of a universal character and may be used in solving continuous problems as well.
Assume we are given a set X of alternatives (from the decision uncertainty region), which are to be examined by q criteria of quantitative and/or qualitative nature. This problem is presented by a pair ![]() where
where ![]() is a vector fuzzy preference relation [24] [28] . In this case, we have
is a vector fuzzy preference relation [24] [28] . In this case, we have
![]() , (34)
, (34)
where ![]() is a membership function of a fuzzy preference relation.
is a membership function of a fuzzy preference relation.
In (34), Rp is defined as a fuzzy set of all pairs of X × X, such that the membership function ![]() represents the degree to which Xk weakly dominates Xl (Xk is not worse than Xl) for the pth criterion.
represents the degree to which Xk weakly dominates Xl (Xk is not worse than Xl) for the pth criterion.
A convincing and natural approach to obtaining matrices Rp is presented in [17] [28] . In particular, the availability of fuzzy or linguistic estimates of alternatives![]() ,
, ![]()
![]() (constructed on the basis of expert estimation or on the basis of aggregating information arriving from different sources of both formal and informal character) with the membership functions
(constructed on the basis of expert estimation or on the basis of aggregating information arriving from different sources of both formal and informal character) with the membership functions![]() ,
, ![]()
![]() permits one, using the expressions (32) and (33), to construct Rp,
permits one, using the expressions (32) and (33), to construct Rp,![]() . Other our approaches to constructing matrices Rp are discussed in [39] [40] .
. Other our approaches to constructing matrices Rp are discussed in [39] [40] .
At the same time, fuzzy preference relations are not a unique form of preference representation. For instance, the authors of [41] [42] indicate eight formats which can be used to establish preferences among analyzed alternatives. It is natural that their application demands a conversion of all formats to a unique format which can be processed and analyzed. Considering the advantages and rationality of the application of fuzzy preference relations for this objective, the results of [17] [43] permit one to construct so-called transformation functions to convert different preference formats to fuzzy preference relations.
The basic procedures to deal with multiple criteria, when preferences are modeled as a vector R of fuzzy preference relations, considered in [17] , are the following: the construction of a set of nondominated alternatives on the basis of simultaneous considering all fuzzy preference relations [24] [28] ; the lexicographic procedure bases on the step-by-step application of fuzzy preference relations for comparing alternatives [16] [28] ; the construction of a set of nondominated alternatives on the basis of the intersection of sets of nondominated alternatives obtained for each fuzzy preference relation [20] .
The indicated procedures have served for developing other techniques: the analysis of alternatives with fuzzy ordering of criteria [17] [24] ; the analysis of alternatives based on the concept of fuzzy majority (based on the application of the so-called OWA operator, originally proposed in [44] ) [17] [40] ; the analysis of alternatives based on an outranking approach (by a means of a fuzzy version of the PROMETHEE [45] ) [17] .
5. Multiobjective Problems with Discrete Variables
When analyzing multiobjective models (![]() models [16] [17] ), a vector of objective functions
models [16] [17] ), a vector of objective functions ![]()
![]() is considered, and the problem consists of optimizing all of them, i.e.,
is considered, and the problem consists of optimizing all of them, i.e.,
![]() (35)
(35)
where L is a feasible region in![]() .
.
The first step in solving the problem (32) is associated with determining a set of Pareto solutions ![]() [46] . This step is useful; however it does not permit one to obtain unique solutions. It is necessary to choose a particular Pareto solution on the basis of information of a decision maker. There are three approaches to using this information [17] [47] : a priori, a posteriori, and adaptive.
[46] . This step is useful; however it does not permit one to obtain unique solutions. It is necessary to choose a particular Pareto solution on the basis of information of a decision maker. There are three approaches to using this information [17] [47] : a priori, a posteriori, and adaptive.
When analyzing multiobjective problems, it is necessary to solve some questions related to normalizing objective functions, selecting principles of optimality, and considering priorities of objectives. Their solution and, therefore, development of multiobjective methods is carried out in the following directions [17] [48] [49] : scalarization techniques, imposing constraints on objectives, utility function method, goal programming, and using the principle of guaranteed result. Without discussing these directions, it is necessary to point out that an important question in the multiobjective analysis is the solution quality. It is considered high if levels of satisfying objective functions are equal or close to each other (harmonious solutions) if we do not differentiate their importance [16] [50] (other directions may lead to solutions with high levels of satisfying some objectives that is reached by low levels of satisfying other objectives, for instance [17] [50] ). From this point of view, it should be recorded the validity and advisability of the direction related to the principle of guaranteed result.
The lack of clarity in the concept of “optimal solution” is the basic methodological complexity in solving multiobjective problems. When applying the Bellman-Zadeh approach to decision making in a fuzzy environment [15] [51] , this concept is defined with reasonable validity: the maximum degree of implementing goals serves as a criterion of optimality. This conforms to the principle of guaranteed result and provides constructive lines in obtaining harmonious solutions. The use of the Bellman-Zadeh approach permits one to realize an effective (from the computational standpoint) as well as rigorous (from the standpoint of obtaining solutions![]() ) method of analyzing multicriteria models [16] . Finally, its use allows one to preserve a natural measure of uncertainty in decision making and to consider indices, criteria, and constraints of qualitative character.
) method of analyzing multicriteria models [16] . Finally, its use allows one to preserve a natural measure of uncertainty in decision making and to consider indices, criteria, and constraints of qualitative character.
When using the Bellman-Zadeh approach, objective functions![]() ,
, ![]() are replaced by fuzzy sets
are replaced by fuzzy sets![]() ,
, ![]() ,
, ![]() , where
, where ![]() is the membership function of
is the membership function of![]() . A fuzzy
. A fuzzy
solution d is defined as ![]() with the membership function
with the membership function
![]() (36)
(36)
The use of (36) allows one to get the solution
![]() (37)
(37)
Therefore, the problem (35) is reduced to search for
![]() . (38)
. (38)
To obtain (38), one needs to build![]() ,
, ![]() , which reflect the capability of achieving own optima
, which reflect the capability of achieving own optima
by![]() ,
, ![]() ,
,![]() . This condition is satisfied if one chooses [17] :
. This condition is satisfied if one chooses [17] :
![]() (39)
(39)
for minimized objective functions or
![]() (40)
(40)
for maximized ones. In (39) and (40), ![]() ,
, ![]() are importance factors for the corresponding objective functions.
are importance factors for the corresponding objective functions.
The construction of (39) or (40) demands the solution of the following problems:
![]() (41)
(41)
![]() (42)
(42)
Thus, the solution of the problem (35) on the basis of the Bellman-Zadeh approach demands analysis of ![]() monocriteria problems (41), (42), and (37), respectively.
monocriteria problems (41), (42), and (37), respectively.
Since ![]() is to belong to
is to belong to![]() , it is necessary to build
, it is necessary to build
![]() , (43)
, (43)
where ![]()
Procedures for solving the problem (37) discussed in [17] provide a line in obtaining ![]() in accordance with (43). Thus, it can be said about equivalence of
in accordance with (43). Thus, it can be said about equivalence of ![]() and
and ![]() and guarantees obtaining harmonious solutions which belong to the Pareto set. This eliminates the necessity of performing a cumbersome stage of constructing the Pareto set and opens up the real possibility of using the multicriteria approach in problems of the short-term planning, operation, and control.
and guarantees obtaining harmonious solutions which belong to the Pareto set. This eliminates the necessity of performing a cumbersome stage of constructing the Pareto set and opens up the real possibility of using the multicriteria approach in problems of the short-term planning, operation, and control.
Finally, the existence of additional conditions (indices, criteria or constraints) of qualitative character, defined by linguistic variables [15] , reduces (38) to
![]() , (44)
, (44)
where![]() ,
, ![]() ,
, ![]() are membership functions of fuzzy values of linguistic variables which reflect these additional conditions.
are membership functions of fuzzy values of linguistic variables which reflect these additional conditions.
Taking the above into account, the solution of the multicriteria discrete problems is reduced to modifying the generalized algorithms of solving discrete optimization problems discussed above to solve the maxmin problem (38).
Although the results of the present Section do not take into account the uncertainty of initial information, they can be used within the framework of a general scheme of multicriteria analysis under information uncertainty [52] [53] with evaluating particular (monocriteria) and aggregated (multicriteria) risks in multiple scenarios.
6. Power Engineering Applications
The described results have found wide applications in the analysis of diverse problems of power engineering, related to improving reliability, quality, and economical feasibility of power supply. These problems are characterized by an extremely high number of variables and, often, by the impossibility of the adequate analytical description of objective functions and constraints.
The following classes of problems of power systems and subsystems have been solved with the use of the results of the present paper:
・ choice and allocation of means for increasing reliability of power supply in distribution systems in different settings;
・ reinforcement (allocation of reactive power sources, allocation of voltage regulators, and reconduction) of distribution systems in different settings;
・ real-time active power control in power systems and subsystems;
・ real-time voltage and reactive power control in distribution systems in different settings.
As an example, it possible to present the solution of the problem of allocating reactive power sources in distribution systems [54] .
Traditionally, problems of reactive power compensation in distribution systems are associated with the selection of locations, sizes, and types of capacitors to minimize the objective function of an economical nature, while the constraints on upper and lower voltage limits at different load levels are satisfied. However, our experience in solving the problems of reactive power compensation shows that the necessity to simultaneously observe constraints on upper and lower voltage limits at different buses creates essential obstacles. It is not uncommon to face situations when these constraints induce empty feasible regions. These obstacles can be avoided by minimizing the objective function of an economical nature as well as the objective function which reflects a volume of poor quality energy consumption. Besides, if the problem is associated with the determination of capacitor types (fixed or switched), the quantity of objectives should be increased.
Taking this into account, the developed computing platform EPODIAN [54] includes tools to solve reactive power compensation problems in monocriteria as well as in multicriteria settings for large-scale distribution networks.
Table 1 demonstrates the results of the application of EPODIAN for the allocation of reactive power sources in a distribution network 13.8/0.22 kV of one of substations of the Energy Company of Minas Gerais (CEMIG).
This network includes 2 feeders with more than 5000 consumers connected to them. The total length of feeders is 729 km . They are modeled by 9660 electrical nodes. In Table 1, I is an initial state, A is a monocriteria solution minimizing the objective function of the economical nature, B is a monocriteria solution minimizing the objective function which reflects a volume of poor quality energy consumption, and C is a multicriteria solution providing a compromise between the solutions A and B. All solutions were obtained less than 30 s on a conventional dual-core desktop PC.
7. Conclusions
In this paper, the generalized algorithms for solving problems of discrete, integer, and Boolean programming are discussed. These algorithms are based on a combination of formal procedures (associated with the method of normalized functions) and informal procedures (related to elements of greedy heuristics). The application of the algorithms allows one to obtain quasi-optimal solutions after a small number of steps, thus overcoming the NP- completeness of discrete optimization problems. Questions of constructing so-called “duplicate” algorithms are considered. Their use as well as the formulation and solution of one and the same discrete optimization problem within the framework of mutually related models serve as means for possible improving the quality of discrete problem solutions.
The approach to solving optimization problems, formalized within the framework of “soft” models containing fuzzy coefficients in objective functions and constraints, has been discussed. This approach is associated with modifying traditional mathematical programming methods and, in particular, the generalized algorithms presented in the paper. It is based on solving one and the same problem within the framework of mutually related models to maximally cut off dominated alternatives from above as well as from below. The subsequent contraction of the decision uncertainty regions is associated with reducing the problem to multiattribute choosing alternatives in a fuzzy environment.
It has shown the possibility of rational solving multiobjective discrete problems on the basis of applying the Bellman-Zadeh approach to decision making in a fuzzy environment and modifying the generalized algorithms presented in the paper.
The results of the paper have found wide applications in the analysis of power engineering problems, related to improving the reliability, quality, and economic efficiency of power supply.
Acknowledgements
This research was supported by the National Council for Scientific and Technological Development of Brazil (CNPq)―grants 305036/2011-4, 307466/2011-6, and the Energy Company of Minas Gerais (CEMIG)―R&D ANEEL Program projects GT480 and D535.
NOTES
*Corresponding author.