New Extension of Unified Family Apostol-Type of Polynomials and Numbers ()
1. Introduction
The generalized Bernoulli polynomials 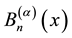 of order
of order 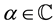 and the generalized Euler polynomials are defined by (see [3] ):
and the generalized Euler polynomials are defined by (see [3] ):
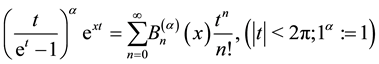 (1.1)
(1.1)
and
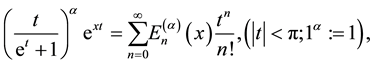 (1.2)
(1.2)
where  denotes the set of complex numbers.
denotes the set of complex numbers.
Recently, Luo and Srivastava [4] introduced the generalized Apostol-Bernoulli polynomials 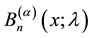 and the generalized Apostol-Euler polynomials
and the generalized Apostol-Euler polynomials 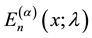 as follows.
as follows.
Definition 1.1. (Luo and Srivastava [4] ) The generalized Apostol-Bernoulli polynomials  of order
of order 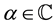 are defined by the generating function
are defined by the generating function

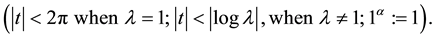 (1.3)
(1.3)
Definition 1.2. (Luo [5] ) The generalized Apostol-Euler polynomials 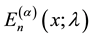 of order
of order 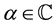 are defined by the generating function
are defined by the generating function

 (1.4)
(1.4)
Natalini and Bernardini [6] defined the new generalization of Bernoulli polynomials in the following definition.
Definition 1.3. The generalized Bernoulli polynomials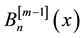 ,
, ![]() , are defined, in a suitable neighbourhood of
, are defined, in a suitable neighbourhood of ![]() by means of generating function
by means of generating function
![]() (1.5)
(1.5)
Recently, Tremblay et al. [7] investigated a new class of generalized Apostol-Bernoulli polynomial as follows.
Definition 1.4. The generalized Apostol-Bernoulli polynomials ![]() of order
of order![]() ,
, ![]() , are defined, in a suitable neighbourhood of
, are defined, in a suitable neighbourhood of ![]() by means of generating function
by means of generating function
![]() (1.6)
(1.6)
Also, Sirvastava et al. [1] introduced a new interesting class of Apostol-Bernoulli polynomials that are closely related to the new class that we present in this paper. They investigated the following form.
Definition 1.5. Let ![]() and
and![]() . Then the generalized Bernoulli polynomials
. Then the generalized Bernoulli polynomials ![]() of order
of order ![]() are defined by the following generating function:
are defined by the following generating function:
![]()
![]() (1.7)
(1.7)
This sequel to the work by Sirvastava et al. [2] introduced and investigated a similar generalization of the family of Euler polynomials defined as follows.
Definition 1.6. Let ![]() and
and![]() . Then the generalized Euler polynomials
. Then the generalized Euler polynomials ![]() of order
of order ![]() are defined by the following generating function
are defined by the following generating function
![]()
![]() (1.8)
(1.8)
It is easy to see that setting ![]() and
and ![]() in (1.8) would lead to Apostol-Euler polynomials defined by (1.4). The case where
in (1.8) would lead to Apostol-Euler polynomials defined by (1.4). The case where ![]() has been studied by Luo et al. [8] .
has been studied by Luo et al. [8] .
In Section 2, we introduce the new extension of unified family of Apostol-type polynomials and numbers that are defined in [9] . Also, we determine relations between some results given in [1] [3] [7] [10] [11] and our results. Moreover, we introduce some new identities for polynomials defined in [9] . In Section 3, we give some basic properties of the new unification of Apostol-type polynomials and numbers. Finally in Section 4, we introduce some relationships between the new unification of Apostol-type polynomials and other known polynomials.
2. Unification of Multiparameter Apostol-Type Polynomials and Numbers
Definition 2.1. Let![]() ,
, ![]() and
and![]() . Then the new unification of Apostol-type polynomials
. Then the new unification of Apostol-type polynomials ![]() are defined, in a suitable neighbourhood of
are defined, in a suitable neighbourhood of ![]() by means of generating function
by means of generating function
![]()
![]() (2.1)
(2.1)
where ![]() is a sequence of complex numbers.
is a sequence of complex numbers.
Remark 2.1. If we set ![]() in (2.1), then we obtain the new unification of multiparameter Apostol-type numbers, as
in (2.1), then we obtain the new unification of multiparameter Apostol-type numbers, as
![]() (2.2)
(2.2)
The generating function in (2.1) gives many types of polynomials as special cases, for example, see Table 1.
Remark 2.2. From NO. 13 in Table 1 and ([9] , Table 1), we can obtain the polynomials and the numbers given in [12] -[16] .
3. Some Basic Properties for the Polynomial ![]()
Theorem 3.1. Let ![]() and
and![]() . Then
. Then
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
Proof. For the first equation, from (2.1)
![]()
using Cauchy product rule, we can easily obtain (3.1).
For the second Equation (3.2), from (2.1)
![]()
Equating the coefficient of ![]() on both sides, yields (3.2).
on both sides, yields (3.2). ![]()
Corollary 3.1. If ![]() in (3.1), we have
in (3.1), we have
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
Theorem 3.2. The following identity holds true, when ![]() and
and ![]() in (2.1)
in (2.1) ![]()
![]() (3.5)
(3.5)
Proof. From (2.1)
![]()
Hence, we can easily obtain (3.5). ![]()
Remark 3.1. If we put![]() ,
, ![]() and
and ![]() in (3.5), then it gives [[12] , Equation (34)],
in (3.5), then it gives [[12] , Equation (34)],
![]()
where ![]() is the unification of the Apostol-type polynomials.
is the unification of the Apostol-type polynomials.
Theorem 3.3. The unification of Apostol-type numbers satisfy
![]() (3.6)
(3.6)
Proof. When ![]() in (2.1), we have
in (2.1), we have
![]()
Using Cauchy product rule, we obtain (3.6). ![]()
Theorem 3.4. The following relationship holds true
![]() (3.7)
(3.7)
where ![]() and
and ![]() and
and![]() ,
,![]() .
.
Proof. Starting with (2.1), we get
![]()
Using Cauchy product rule on the right hand side of the last equation and equating the coefficients of ![]() on both sides, yields (3.7).
on both sides, yields (3.7). ![]()
Using No. 13 in Table 1, we obtain Nörlund’s results, see [17] and Carlitz’s generalizations, see [18] by our approach in Theorem 3.5 and Theorem 3.6 as follows
Theorem 3.5. For![]() , we have
, we have
![]() (3.8)
(3.8)
![]() (3.9)
(3.9)
Proof. For the first equation and starting with (2.1), we get
![]()
Equating the coefficients of ![]() on both sides, yields (3.8).
on both sides, yields (3.8).
For the second equation and starting with (2.1), we get
![]()
then, we have
![]()
Equating coefficients of ![]() on both sides, yields (3.9).
on both sides, yields (3.9). ![]()
Theorem 3.6. For ![]() and
and ![]() we have
we have
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
Proof. For the first equation and starting with (2.1), we get
![]()
Equating the coefficients of ![]() on both sides, yields (3.10).
on both sides, yields (3.10).
Also, It is not difficult to prove (3.11). ![]()
4. Some Relations between ![]() and Other Polynomials and Numbers
and Other Polynomials and Numbers
In this section, we give some relationships between the polynomials ![]() and Laguerre polynomials, Jacobi polynomials, Hermite polynomials, generalized Stirling numbers of second kind, Stirling numbers and Bleimann-Butzer-hahn basic.
and Laguerre polynomials, Jacobi polynomials, Hermite polynomials, generalized Stirling numbers of second kind, Stirling numbers and Bleimann-Butzer-hahn basic.
Theorem 4.1. For![]() ,
, ![]() and
and![]() , we have relationship
, we have relationship
![]() (4.1)
(4.1)
between the new unification of Apostol-type polynomials and generalized Stirling numbers of second kind, see [19] .
Proof. Using (3.4) and from definition of generalized Stirling numbers of second kind, we easily obtain (4.1). ![]()
Theorem 4.2. For![]() ,
, ![]() and
and![]() , we have the relationship
, we have the relationship
![]() (4.2)
(4.2)
between the new unification of Apostol-type polynomials and Stirling numbers of second kind.
Proof. Using (3.4) and from definition of Stirling numbers of second kind (see [20] ), we easily obtain (4.2). ![]()
Theorem 4.3. The relationship
![]() (4.3)
(4.3)
holds between the new unification of multiparameter Apostol-type polynomials and generalized Laguerre polynomials (see [7] , No. (3), Table 1).
Proof. From (3.4) and substitute
![]()
then we get (4.3). ![]()
Theorem 4.4. For![]() . The relationship
. The relationship
![]()
![]() (4.4)
(4.4)
holds between the new unification of Apostol-type polynomials and Jacobi polynomials (see [21] , p. 49, Equation (35)).
Proof. From (3.4) and substitute
![]()
then we get (4.4). ![]()
Theorem 4.5. The relationship
![]() (4.5)
(4.5)
holds between the new unification of Apostol-type polynomials and Hermite polynomials (see [7] , No. (1) Table 1).
Proof. From (3.4) and substitute
![]()
then we get (4.5). ![]()
Theorem 4.6. When![]() ,
, ![]() ,
, ![]() and
and ![]() in (9) and for
in (9) and for![]() ,
,
![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
,
![]() ,
, ![]() , we have the following relationship
, we have the following relationship
![]() (4.6)
(4.6)
between the new unified family of generalized Apostol-Euler, Bernoulli and Genocchi polynomials, and
![]() (the generalized Lah numbers) (see [22] ).
(the generalized Lah numbers) (see [22] ).
Proof. From [9] , Equation (2.1),
![]()
Equating the coefficients of ![]() on both sides, yields (4.6).
on both sides, yields (4.6). ![]()
Using No. 13 in Table 1 (see [9] ) and the definition of the unified Bernstein and Bleimann-Butzer-Hahn basis (see [23] ),
![]() (4.7)
(4.7)
where![]() ,
, ![]() ,
, ![]() , we obtain the following theorem.
, we obtain the following theorem.
Theorem 4.7. For ![]() we have relationship
we have relationship
![]() (4.8)
(4.8)
between the unified Bernstein and Bleimann-Butzer-Hahn basis, the new unified family of generalized Apostol-Bernoulli, Euler and Genocchi polynomials (see [9] ) and generalized Stirling numbers of first kind (see [19] ).
Proof. From (2.1) and (4.7) and with some elementary calculation, we easily obtain (4.8). ![]()