1. Introduction
All graphs considered in this paper are finite, loopless, and without multiple edges. For a graph G, we refer to 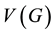 and
and 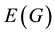 as the vertex set and the edge set, respectively. The cardinality of
as the vertex set and the edge set, respectively. The cardinality of 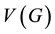 is called the order of G, denoted by
is called the order of G, denoted by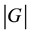 . The (open) neighborhood
. The (open) neighborhood 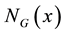 of a vertex x is the set of vertices adjacent to x in G, and the close neighborhood
of a vertex x is the set of vertices adjacent to x in G, and the close neighborhood 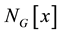 is
is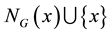 . A vertex x is said to be a leaf if
. A vertex x is said to be a leaf if . A vertex v of G is a support vertex if it is adjacent to a leaf in G. Two distinct vertices u and v are called duplicated if
. A vertex v of G is a support vertex if it is adjacent to a leaf in G. Two distinct vertices u and v are called duplicated if . Note that u and v are duplicated vertices in a tree, and then they are both leaves. The n-path
. Note that u and v are duplicated vertices in a tree, and then they are both leaves. The n-path 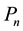 is the path of order
is the path of order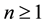 . For a subset
. For a subset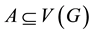 , the induced subgraph induced by A is the graph
, the induced subgraph induced by A is the graph 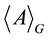 with vertex set A and the edge set
with vertex set A and the edge set![]() , the deletion of A from G is the graph
, the deletion of A from G is the graph ![]() by removing all vertices in A and all edges incident to these vertices and the complement of A is the set
by removing all vertices in A and all edges incident to these vertices and the complement of A is the set![]() . For notation and terminology in graphs we follow [1] in general.
. For notation and terminology in graphs we follow [1] in general.
A set ![]() is an independent set of G if no two vertices of I are adjacent in G. The independence number
is an independent set of G if no two vertices of I are adjacent in G. The independence number ![]() of G is the maximum cardinality among all independent sets of G. If I is an independent set of G with cardinality
of G is the maximum cardinality among all independent sets of G. If I is an independent set of G with cardinality![]() , we call I an
, we call I an ![]() -set of G. If I is an
-set of G. If I is an ![]() -set of G containing all leaves of G, we call I an
-set of G containing all leaves of G, we call I an ![]() -set of G.
-set of G.
The independence problem is to find an ![]() -set in G. The problem is known to be NP-hard in many special classes of graphs. Over the past few years, several studies have been made on independence (see [2] -[6] ). For
-set in G. The problem is known to be NP-hard in many special classes of graphs. Over the past few years, several studies have been made on independence (see [2] -[6] ). For
any tree T of order![]() , it is easy to see that
, it is easy to see that![]() . In addition, if there are duplicated leaves in a tree, then these duplicated leaves are all lying in every maximum independent set. In this paper, we will show that if T is a tree of order
. In addition, if there are duplicated leaves in a tree, then these duplicated leaves are all lying in every maximum independent set. In this paper, we will show that if T is a tree of order ![]() without duplicated leaves, then
without duplicated leaves, then![]() . Moreover, we constructively
. Moreover, we constructively
characterize the extremal trees T of order![]() , which are without duplicated leaves, achieving these upper bounds.
, which are without duplicated leaves, achieving these upper bounds.
2. The Upper Bound
In this section, we will show a sharp upper bound on the independence number of a tree T without duplicated leaves.
Lemma 1 If H is an induced subgraph of G, then![]() .
.
Proof. If S is an ![]() -set of H, then S is an independent set of G. It follows that
-set of H, then S is an independent set of G. It follows that![]() .
. ![]()
Lemma 2 ([4] ) If T is a tree of order![]() , then
, then![]() .
.
Lemma 3 ([5] ) If T is a tree of order![]() , then there exists an
, then there exists an ![]() -set of T.
-set of T.
Lemma 4 For an integer![]() ,
,![]() .
.
Proof. It is straightforward to check that ![]() for
for![]() . Let
. Let![]() . Since Pn is a tree of order
. Since Pn is a tree of order![]() , by Lemma 2, we have that
, by Lemma 2, we have that![]() . Suppose that there exists an independent set I of Pn with
. Suppose that there exists an independent set I of Pn with![]() , then there exists i,
, then there exists i, ![]() , such that
, such that ![]() and
and![]() . This is a contradiction, therefore we obtain that
. This is a contradiction, therefore we obtain that![]() .
. ![]()
Theorem 1 If T is a tree of order ![]() without duplicated leaves, then
without duplicated leaves, then![]() .
.
Proof. We prove it by induction on![]() . By Lemma 4 and T is a tree without duplicated leaves, it’s true for all
. By Lemma 4 and T is a tree without duplicated leaves, it’s true for all![]() . For all
. For all ![]() we assume that the assertion is true for all
we assume that the assertion is true for all![]() . Suppose that T is a tree of order
. Suppose that T is a tree of order ![]() without duplicated leaves and x is a leaf lying on a longest path of T. Let
without duplicated leaves and x is a leaf lying on a longest path of T. Let![]() . Since T has no duplicated leaves, this implies that
. Since T has no duplicated leaves, this implies that![]() , say
, say![]() . Let
. Let![]() , then T' is a tree of order
, then T' is a tree of order![]() . For the case in which T' has no duplicated leaves, by induction hypothesis, we have that
. For the case in which T' has no duplicated leaves, by induction hypothesis, we have that
![]() . Since an
. Since an ![]() -set of T', together with
-set of T', together with![]() , form an
, form an ![]() -set of T. Therefore we obtain that
-set of T. Therefore we obtain that![]() . For the other case in which T' has duplicated leaves z and
. For the other case in which T' has duplicated leaves z and![]() , then
, then ![]() is a tree of order
is a tree of order ![]() without duplicated leaves. By induction hypothesis, we have that
without duplicated leaves. By induction hypothesis, we have that![]() . Since an
. Since an ![]() -set of
-set of![]() , together with
, together with![]() , form an
, form an ![]() -set of T. Therefore, we obtain that
-set of T. Therefore, we obtain that![]() . Hence we conclude that
. Hence we conclude that
![]() .
.
Note that the result in Theorem 1 is sharp and some such T are illustrated below.
3. Extremal Trees
Let ![]() be the class of all trees T of order
be the class of all trees T of order ![]() without duplicated leaves such that
without duplicated leaves such that![]() .
.
We will constructively characterize these extremal trees. Let ![]() and
and![]() , respectively, denote the collections of all leaves and all support vertices of T. First, we define four operations on a tree T of order
, respectively, denote the collections of all leaves and all support vertices of T. First, we define four operations on a tree T of order ![]() as follows, where I is an
as follows, where I is an ![]() -set of T.
-set of T.
Operation O1. Join a vertex ![]() of
of ![]() to a vertex
to a vertex ![]() of
of ![]() such that
such that![]() , where
, where ![]() (mod 3).
(mod 3).
Operation O2. Join a vertex ![]() of
of ![]() to a vertex
to a vertex ![]() of
of ![]() such that
such that![]() , where
, where ![]() (mod 3).
(mod 3).
Operation O3. Join a vertex u of ![]() to a leaf
to a leaf ![]() of
of ![]() (say
(say![]() ) such that
) such that![]() , where
, where ![]() (mod 3).
(mod 3).
Operation O4. Join a vertex ![]() of T to a leaf v3 of P3 (say
of T to a leaf v3 of P3 (say![]() ) such that
) such that![]() .
.
Lemma 5 Suppose that ![]() for
for![]() .If I is an
.If I is an ![]() -set of T, then
-set of T, then
![]()
Proof. It’s true for all![]() . So we assume that
. So we assume that![]() . Since I is an
. Since I is an ![]() -set of T, this implies that
-set of T, this implies that![]() . By Theorem 1, we have that
. By Theorem 1, we have that
![]()
Hence we obtain that![]() . Let
. Let![]() . Note that
. Note that ![]() and
and
![]() for every i. In addition,
for every i. In addition, ![]() , these imply that
, these imply that![]() . Thus we obtain that
. Thus we obtain that![]() . It follows that
. It follows that
![]()
This completes the proof. ![]()
Lemma 6 Let ![]() be a tree of order
be a tree of order ![]() with an
with an ![]() -set I. Suppose that T' is obtained from T by Operation O1, then
-set I. Suppose that T' is obtained from T by Operation O1, then ![]() is a tree of order
is a tree of order ![]() and
and ![]() is an
is an ![]() -set of T'.
-set of T'.
Proof. Suppose that ![]() is a tree of order
is a tree of order ![]() (mod 3) with an
(mod 3) with an ![]() -set I, by Lemma 5, then
-set I, by Lemma 5, then![]() . Let T' be the tree obtained from T by Operation O1. Since
. Let T' be the tree obtained from T by Operation O1. Since![]() , this implies that u is not a support vertex of T and T' is a tree of order
, this implies that u is not a support vertex of T and T' is a tree of order ![]() without duplicated leaves. On the other hand,
without duplicated leaves. On the other hand, ![]() is an independent
is an independent
set of ![]() with
with ![]() such that
such that![]() , where
, where ![]() (mod 3). Hence
(mod 3). Hence![]() . In conclusion,
. In conclusion, ![]() is a tree of order
is a tree of order ![]() with an
with an ![]() -set IO1.
-set IO1. ![]()
Lemma 7 Let ![]() be a tree of order
be a tree of order ![]() with an
with an ![]() -set I such that
-set I such that![]() . If
. If ![]() is obtained from T by Operation O2, then
is obtained from T by Operation O2, then ![]() is a tree of order
is a tree of order ![]() and
and ![]() is an
is an ![]() -set of
-set of![]() .
.
Proof. Note that such a tree T exists, as, for instance, the tree in Figure 1 is as desired. If ![]() is a tree of order
is a tree of order ![]() (mod 3) with an
(mod 3) with an ![]() -set I such that
-set I such that![]() . Let T' be the tree obtained from T by Operation O2. Since u is not a support vertex of T, this implies that T' is a tree of order
. Let T' be the tree obtained from T by Operation O2. Since u is not a support vertex of T, this implies that T' is a tree of order ![]() without duplicated leaves. And
without duplicated leaves. And ![]() is an independent set of T' with
is an independent set of T' with ![]() such that
such that
![]() , where
, where ![]() (mod 3). Hence
(mod 3). Hence
![]() . In conclusion,
. In conclusion, ![]() is a tree of order
is a tree of order ![]() with an
with an ![]() -set IO2.
-set IO2. ![]()
Lemma 8 Let ![]() be a tree of order
be a tree of order ![]() with an
with an ![]() -set I. If T' is obtained from T by Operation O3, then
-set I. If T' is obtained from T by Operation O3, then ![]() is a tree of order
is a tree of order ![]() and IO3 is an
and IO3 is an ![]() -set of T'.
-set of T'.
Proof. Note that T' is a tree of order n + 2 without duplicated leaves. And IO3 is an independent set of T' with
![]() such that
such that![]() , where
, where ![]() (mod 3). Hence
(mod 3). Hence![]() . In conclusion,
. In conclusion, ![]() is a tree of order
is a tree of order ![]() with an
with an ![]() - set IO3.
- set IO3. ![]()
Lemma 9 Let ![]() be a tree of order
be a tree of order ![]() with an
with an ![]() -set I. If T' is obtained from T by Operation O4, then
-set I. If T' is obtained from T by Operation O4, then ![]() is a tree of order
is a tree of order ![]() and IO4 is an
and IO4 is an ![]() -set of T'.
-set of T'.
Proof. Note that T' is a tree of order ![]() without duplicated leaves. And IO4 is an independent set of T' with
without duplicated leaves. And IO4 is an independent set of T' with
![]() such that
such that![]() . Hence
. Hence
![]() . In conclusion,
. In conclusion, ![]() is a tree of order
is a tree of order ![]() with an
with an ![]() -set IO4.
-set IO4. ![]()
Let ![]() be the class of all trees obtained from
be the class of all trees obtained from ![]() or
or ![]() by a finite sequence of Operations O1-O4. Suppose that
by a finite sequence of Operations O1-O4. Suppose that![]() , we will show that
, we will show that![]() .
.
Theorem 2 T is in ![]() if and only if T is in
if and only if T is in![]() .
.
Proof. If T is in![]() , by Lemmas 6, 7, 8 and 9, then T is in
, by Lemmas 6, 7, 8 and 9, then T is in![]() . Now, we want to show the converse by contradiction. Suppose to the contrary that there exists a tree
. Now, we want to show the converse by contradiction. Suppose to the contrary that there exists a tree ![]() and
and ![]() such that
such that ![]() is as small as possible. We can see that
is as small as possible. We can see that![]() . Let
. Let ![]() be a longest path of T. Then
be a longest path of T. Then ![]() and
and ![]() is a tree of order
is a tree of order![]() . We consider two cases.
. We consider two cases.
Case 1. T' has no duplicated leaves.
For an ![]() -set I of T,
-set I of T, ![]() is an independent set of T', this implies that
is an independent set of T', this implies that![]() . By
. By
Theorem 1, we have that![]() . Then
. Then ![]() and
and ![]() (mod 3). This follows that
(mod 3). This follows that![]() , where
, where
![]() (mod 3), by hypothesis,
(mod 3), by hypothesis,![]() . Note that T can be obtained from
. Note that T can be obtained from ![]() by Operation O3, this implies that
by Operation O3, this implies that![]() , which is a contradiction.
, which is a contradiction.
Case 2. T' has duplicated leaves z and z'.
Let![]() . Then
. Then ![]() is a tree of order
is a tree of order![]() . Since z' is a leaf of T, this implies that z and z' are in every
. Since z' is a leaf of T, this implies that z and z' are in every ![]() -set of T. For an
-set of T. For an ![]() -set I of T,
-set I of T, ![]() is an independent set of
is an independent set of![]() , thus
, thus ![]() . By Theorem 1, we have that
. By Theorem 1, we have that
![]() . Then
. Then![]() . This fol-
. This fol-
lows that![]() , where
, where![]() , by hypothesis,
, by hypothesis,![]() . Note that T can be obtained from
. Note that T can be obtained from ![]() by Operation O4, this implies that
by Operation O4, this implies that![]() , which is a contradiction.
, which is a contradiction.
By Cases 1 and 2, we conclude that T is in![]() , then T is in
, then T is in![]() .
. ![]()
Now, we obtain the main theorem in this paper.
Theorem 3 Suppose that T is a tree of order ![]() without duplicated leaves, then
without duplicated leaves, then![]() . Furthermore, the equality holds if and only if
. Furthermore, the equality holds if and only if![]() .
.