Credit Derivative Valuation and Parameter Estimation for Multi-Factor Affine CIR-Type Hazard Rate Model ()
1. Introduction
The major credit problems and significant failures faced by banks during Global Financial Crises, for example the recent financial crisis or credit crisis of 2007-2008 [1] , and the failures of large prestigious institutions such as Lehman Brothers, Bear Sterns, Fannie Mae and Freddie Mac [2] [3] , have highlighted the importance of modeling and providing for a credit risk quantifier. Credit Risk is the risk that a borrower (company, individual, sovereign government) will default on any type of debt by failing to meet its financial obligation. It emerges to be not just the traditional risk that lenders or ownership of the bonds or loans (example financial institutions) spare when lending out money, but also a financial contract traded (or exchanged) around the world.
The designation or development of new products, such as Credit Derivatives (CDs), by all investors and financial institutions to reduce or remove any Credit Risk arises from lenders or bondholders (example banks), and to allow banks to deliver more loans seemed to want a share in it. The most widely used product of CDs is the Credit Default Swap (CDS). The Credit Default Swap is a contract entered between two parties that provide a protection against losses occurring due to a default event of a certain entity. Since its introduction in the mid-1990s, the growth of the global market has been overwhelming: for example, the market size for CDS almost doubled biannually from 1996 to 2004, and even quadrupled to over a peak notional outstanding amount of US $20 trillion during 2004-2006 [4] .
The measurement or modeling of credit risk, however, provides its own set of challenges. There exist many ways of modeling credit risk [5] -[7] with the implication that banks can face a quandary of choosing the models.
The main point of this paper is to consider how the default is modeled for estimating the value of Credit Default Swaps. There are different ways for modeling the Credit Derivatives, typically characterized by how they characterize the default event. Duffie and Signeton [8] suggest that the approach in which the default is indicated or characterized by a hazard rate is largely related to the distribution of default time. Their approach suggests that the defaultable claims can be priced the same way as the non-default claims. Using the Duffie and Signeton’s framework, David and Mavroidis [9] suppose that the hazard rate is a Gaussian model with time-dependent deterministic drift to revise the valuation of the Credit Default Swap. Aonuma and Nakagawa [10] extend David and Mavroid’s work to model the hazard rate in form of affine type or quadratic Gaussian type term structure model, such as Vasick model, and give the valuation formula for the Credit Default Swap that contains basket type or counter party risk [11] [12] . In this paper, we consider the default intensity model which takes the hazard rate as principal factor and distributed as the multi-factor Cox, Ingersoll and Ross (CIR) model. It is widely agreed that a single factor model is unable to capture the yield curve precisely and more economic factors should be included in defaultable bond pricing (e.g. Chen and Scott, 1993). Adding more factors into the latent model yields smaller computation error than those in single-factor processes. This alteration is prompted by empirical evidence which proposes that single factor Affine Term Structures are unable to describe or explain the dynamics of the US term structure.
The paper is organized as follows. In Section 2, we discuss how to estimate hazard rate which follows the dynamic of the multi-factor CIR-type model using the relationship between credit spread and hazard rate, that, is necessary for switching the market credit spread data (collecting directly from the market data) into the multi- factor CIR-type Hazard rate data. We analyze the hazard rate function of single-factor and two-factor CIR-type models and give some results. In Section 3, we follow the framework proposed by David and Mavroidis [9] , Aonuma and Nakagawa [10] , and Richard White [13] to give the main techniques used to value credit default swap under the multi-factor CIR type hazard rate. These are done for the only one defaultable bond issued by the company. Here the explicit value of the credit default swap for both the fixed side, and the recovery side, are established in a quite general form. Section 4 treats the parameter estimation associated with the single factor hazard rate type CIR model using the Generalized Moment Method. And we shall investigate 20 South African firm’s debt terms, with different rating from AAA to BBB and different market credit spread for maturity one year, three years and five years to analyze and estimate parameters associated with the stochastic single-factor hazard rate CIR-type model.
2. Multifactor Affine Type Hazard Rate Models
In this section, we discuss how to estimate hazard rate type Multi-factor CIR model. Using the relationship between credit spread and hazard rate, it is possible to convert the market credit spread data (collected directly from the market data) into CIR (or Vasicek) multi-factor type Hazard rate data. Our first analysis, thus, assumes the risk-free interest rate r to be independent of all the hazard rates. Therefore the occurrence of default is not correlated with bond prices. This assumption implies that the level of default is cause by some factors affecting the issuer, not the level of risk-free interest rate.
Multi-factor affine models of the term structure represent the yield of securities as affine function of a vector of n unobservable state variable , which is given by the multidimensional diffusion process follows:
, which is given by the multidimensional diffusion process follows:
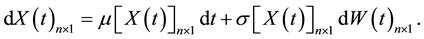 (1)
(1)
CIR Affine Models
A model is
CIR
affine if all state variables 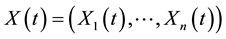 are independent process of the single factor
CIR
-type.
are independent process of the single factor
CIR
-type.
Therefore, for 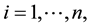
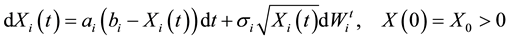 , (2)
, (2)
where the parameters ?i, bi and σi are viewed as the speed of mean reversion, the long-term mean or the mean reversion level and the volatility respectively, and  are independent Wiener process (or standard Brownian motions). As the model is affine in every factor, the defaulatable zero coupon bond prices
are independent Wiener process (or standard Brownian motions). As the model is affine in every factor, the defaulatable zero coupon bond prices 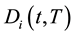 for the
for the 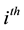 one-factor CIR-process can be written in affine form
one-factor CIR-process can be written in affine form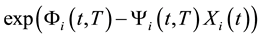 .
.
Due to the independence of factors it is subsequently to derive the below formula. The price 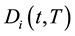 of a zero-coupon defaultable bond with notional value 1 is given by
of a zero-coupon defaultable bond with notional value 1 is given by
 (3)
(3)
where , and δ is the recovery rate, and the instantaneous hazard rate γ follows multi factor CIR and assume to be defined as
, and δ is the recovery rate, and the instantaneous hazard rate γ follows multi factor CIR and assume to be defined as
 . (4)
. (4)
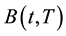 is a price at time t of a zero free coupon bond with maturity T and
is a price at time t of a zero free coupon bond with maturity T and
 (5)
(5)
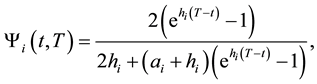 (6)
(6)
![]() (7)
(7)
At time t the credit spread, viewed as the difference between the default adjusted interest rate and the risk- free interest rate is given by ![]() [10] .
[10] .
We are now in a position to define the relationship between the credit spread and hazard rate process. This is useful in converting the credit spread data given from market data into the hazard rate.
Lemma 2.1. Let ![]() and
and ![]() be as in (3), for
be as in (3), for![]() , the credit spread process
, the credit spread process ![]() for the bond with maturity T satisfies the relationship:
for the bond with maturity T satisfies the relationship:
![]() (8)
(8)
![]() (9)
(9)
Proof 2.2. Note that it is impossible to estimate the recovery rate δ and the hazard rate γ separately from the credit spread: knowing δ (given by another technique), we may determine the parameters of the hazard rateγ.
We therefore need to determine the distribution of the random variable![]() . To manage this, weassume the hazard rate process is distributed as CIR multi-factor modelas defined in(4). The quick way to determine
. To manage this, weassume the hazard rate process is distributed as CIR multi-factor modelas defined in(4). The quick way to determine![]() is to suitably transform it as
is to suitably transform it as
![]() .
.
This is contained in the formula of the bond price (for δ = 0), which is the expectation of the exponential of minus the integral of the short term process. Analogously to the work of the CIR model and Bond price under CIR, the CIR formula for the price of a zero-coupon bond is
![]() .
.
where
![]()
![]()
![]()
This new process immediately yields
![]()
Given the relation of credit spread (8), we obtain
![]() (10)
(10)
![]() (11)
(11)
Equivalently, the hazard rate in a CIR-type model is given by
![]() (12)
(12)
where ![]()
![]()
![]()
Example
For the Single-factor model, the hazard rate CIR-type model is given by
![]() (13)
(13)
where
![]()
![]()
![]()
Figure 1 illustrates the hazard rate function of time of twenty years from now on, and distributed as the single factor CIR-type model; given the market price of credit spread. We took the volatility to be σ = 0.9. The figure shows that the hazard rate function, is increasing from time t = 0 to t = 10 years, 14 to 16 and 18 to 20. Intuitively, this means that the probability of defaulting in any of these periods between 0 and 10, 14 and 16, and 18 and 20 years (conditional on not having defaulted until then) increases as time goes on. Upward sloping function in these periods mean that the market is implying not only that the firms are more likely to default with every year that goes by, but also that likelihoods in each year from 0 to 10, 14 to 16 and 18 to 20 years, are ever increasing. Credit risk is therefore getting increasingly worse for every year into the future. From the period of 10 to 14 years and 16 to 18 years, the hazard rate function is decreasing as can be see when looking at Figure 1. This does not mean that the cumulative probability of default decreases; rather it implies a higher conditional probability of default (hazard rate) in earlier years with a lower conditional probability of default in later period.
For the two-factor model, the hazard rate CIR-type model is given by
![]() (14)
(14)
where ![]() and
and ![]() for i = 1, and
for i = 1, and ![]() and
and ![]() for i = 2.
for i = 2.
Figure 2 illustrates the hazard rate function of time of twenty years from now on, and distributed as the
![]()
Figure 1. Single factor hazard rate function ![]() with σ = 0.9.
with σ = 0.9.
![]()
Figure 2. Two factor hazard rate function ![]() with σ = 0.9.
with σ = 0.9.
two factors CIR-type model; given the market price of credit spread. We took the volatility to be σ = σ1 = σ2 = 0.9. The figure shows that the hazard rate function, is slightly variant (slightly increasing and decreasing from time t = 0 to t = 18) and increasing from t = 18 to t = 20. This two factors CIR-type mode (Figure 2) gives a better result compared to the single factor model (Figure 1).
3. Framework
Given the filtered space ![]() and a standard Brownian motion W on space, we let
and a standard Brownian motion W on space, we let ![]()
be a two dimensional Brownian filtration and denote by τ a non-negative random default time. We assume the 2-dimensional ![]() -Brownian motion
-Brownian motion![]() , that means
, that means ![]() satisfies the regular conditions of com- pleteness and right-continue. Also
satisfies the regular conditions of com- pleteness and right-continue. Also ![]() is the smallest filtration which made W and
is the smallest filtration which made W and ![]() adapted. If we sup-
adapted. If we sup-
pose that we are given an auxiliary reference filtration ![]() such that
such that![]() , then all the possible information available at time t is captured by the filtration
, then all the possible information available at time t is captured by the filtration![]() , it is a right continuousτ and also is an
, it is a right continuousτ and also is an![]() -stopping time. In the above
-stopping time. In the above![]() is an abbreviation for
is an abbreviation for![]() .
.
The following important lemmas are introduced for further evaluation of credit default swaps
Lemma 3.1. Assume that the hazard rate process γtis a non-negative ![]() progressively measurable. Then the process
progressively measurable. Then the process
![]() (15)
(15)
is a Martingale on![]() .
.
Lemma 3.2. Assume that, for![]() ,
, ![]() be a
be a ![]() -measurable and
-measurable and ![]() -integrable random variable, then we have
-integrable random variable, then we have
![]() (16)
(16)
Corollary 3.3. For any bounded ![]() predictable process Z
predictable process Z
![]() (17)
(17)
Proof [14] .
4. Definition of CDS and Pricing CDS
We follow the framework of David and Mavroidis [10] , Richard White [13] , and Hidetoshi et al. [15] to value the CDS, starting first, by defining the credit default swaps, specifying the rule of the default swap and pricing CDS.
4.1. Definition of CDS
A credit default swap is an agreement designed between two parties that provide a protection or assurance against losses occurring due to a default event of a certain entity (Figure 3).
One party agreed to buy protection called protection buyer B (e.g., a firm) and provides a regular payment![]() until the credit event occurs or at maturity of the contract (at expected time
until the credit event occurs or at maturity of the contract (at expected time![]() ), the other is the seller of the protection S. Typically banks or insurance companies will assume the credit risk and deliver the difference between the notional value and some recovered value δ from the bond issuer for the owner of the bond B, if the credit event of the bond issuer happens before the maturity date T2.
), the other is the seller of the protection S. Typically banks or insurance companies will assume the credit risk and deliver the difference between the notional value and some recovered value δ from the bond issuer for the owner of the bond B, if the credit event of the bond issuer happens before the maturity date T2.
The risky bond that the buyer B holds permits a fixed coupon ![]() at each adopted time
at each adopted time![]() except when the default even occurs.
except when the default even occurs.
A credit default swap agreement includes a fixed premium leg or fixed side and a recovery side (or contingent default leg).
・ The fixed side corresponds to the series of payments made by the buyer B of the CDS-contract to the protection seller S of the contract up to the maturity time, unless a bankruptcy event or other credit event perturbs the contingent payment on a CDS.
・ The recovery side corresponds to the net payment delivered by the counter party protection seller S to the protection buyer in case of such default event happens.
The main goal of valuation of CDS is to obtain equilibrium premium (or regular payment) ci’s paid periodically by the reference holder, which is followed from the equality of the value between fixed premium leg and contingent default leg. Consider the risk-free interest rate r be independent of all factors related to credit risk, alike default time and the hazard rates. This assumption implies that we can value default swap in term of the default-free zero coupon bond’s prices as follows.
4.2. The Price of the Fixed Side
Since all payments are evaluated at t = 0 and no payment is made after any default event occurs, the actual value of the fixed side ![]() is basically defined by:
is basically defined by:
![]() (18)
(18)
where r is the short rate interest and ![]() is the expectation value under the risk neutral measure
is the expectation value under the risk neutral measure![]() . It follows that
. It follows that
![]()
is an explicit value of the fixed side, when the hazard rate function γ(t) is distributed as a multi-factor CIR model.
where
![]()
![]()
![]()
The Price of the Contingent Default Leg (Recovery Side)
Let ![]() be the cum-coupon amount of the underlying defaultable bond and its value is given by
be the cum-coupon amount of the underlying defaultable bond and its value is given by
![]()
where ![]() is a fixed coupon,
is a fixed coupon, ![]() the short rate interest and γuthe hazard rate process. It is supposed that the fixed premium leg to the contract can recover the specific amount
the short rate interest and γuthe hazard rate process. It is supposed that the fixed premium leg to the contract can recover the specific amount![]() , when the default event occurs to the issuer of the bond, at default time
, when the default event occurs to the issuer of the bond, at default time![]() . Then, the price of the recovery side has been defined by Hidetoshi Nakagawa [14] as
. Then, the price of the recovery side has been defined by Hidetoshi Nakagawa [14] as
![]() (19)
(19)
This equation can be evaluated separately as
![]()
By Corollary 3.3, Lemma 3.2 and using hazard rate mean reversion. And for second term in (19) with application of Corollary 3.3
![]()
Therefore,
![]()
where
![]()
![]()
![]()
This is the price of the recovery side or contingent default leg for the hazard rate multi-factor CIR type. Given the value of the default free zero coupons bond ![]() its explicit value can be derived.
its explicit value can be derived.
5. Analysis and Numerical Results
We shall estimate parameters associated with hazard rate models using the Moment Method. We investigate 20 South African firm’s debt terms, with different rating from AAA to BBB and different market credit spread for maturity one year, three years and five years as shown in Table 1. The results in the rest of this paper are based on the South Africa credit spread data in Table 1 given in [16] . Those credit spreads were calculated using the one year, three year and five year debt terms of 20 South Africa companies, rated AAA to BBB. For a debt term of 5 years the spread varies from 6 bp to 297 bp in the banking sector and from 3 bp to 85 bp in other sectors.
![]()
Table 1. Hazard rate parameters (σ and ?) for CIR-type model.
An asterisk * indicates that the firm is in the banking sector.
More specifically, using a debt term of 3 years, the credit spreads of AA-rated companies vary between 2 and 12 bps whereas observed spreads in the South African market at the time of writing and in general, vary between 30 and 60 bps [16] . We analyze and estimate the parameters for a single or one factor CIR model described previously.
5.1. Parameter Estimation with CIR Model
We recall that the parameter of hazard rate process can be estimated from historical market data of credit spread. In the special cases, such as: -Vasicek model, and CIR model, (except for the recovery rate δ), we have to secure the parameters estimator for hazard rate ?, b and σ. Meaning that we need to have at least four different credit spread ![]() from market data of the firm. Nevertheless, it is not easy to g et al. those data since only a limited number of bonds are issued by each company and the amount traded in the marketplace is not enough to evaluate all the parameters. Thus, we cannot simplify the task by supposing some exogenous parameters and finding the remaining ones implicitly. Hence, we consider the procedure of estimating parameters when only one defaultable bond issued by the company. As before we shall treat the CIR type model below (the same work can be done with the Vasicek model).
from market data of the firm. Nevertheless, it is not easy to g et al. those data since only a limited number of bonds are issued by each company and the amount traded in the marketplace is not enough to evaluate all the parameters. Thus, we cannot simplify the task by supposing some exogenous parameters and finding the remaining ones implicitly. Hence, we consider the procedure of estimating parameters when only one defaultable bond issued by the company. As before we shall treat the CIR type model below (the same work can be done with the Vasicek model).
Parameter Estimation
There exist different methods of estimating the parameters, including the implied volatility which is used in option valuation. Typically they are characterized or evaluated from the historical data. Though we consider the CIR processes in particular, we note that a similar procedure is possible for other models (Vasicek, et). We follow [10] to estimate the parameters, such as recovery rate δ and the long-term mean b using the South Africa data:
・ Characteristic of the long-term mean hazard rate type CIR process b.
Following the assumption that the long-term mean hazard rate process is similar for the same category of industry and the rating of the same class, we consider the estimation of b as the mean value of the probability of default on every category of industry and rating collected from rating agencies such as Standard & Poor, Moody’s and Fitch. We assume the long-term mean b is 10%.
・ Rule of estimating recovery rate δ.
Moody Agency’s database includes detailed bond prices information after default, the historical market price of the bond for 30 days (one month) after the firm experienced the default event. This is viewed as the recovery rate from the default bond. Basically, the average of debt differs from issuers to issuers (or from firm to firm), in this discussion we assume that the recovery rate of the same class of financial rating and the same class of industry are shared and regard as the recovery rate δ of the firm. That is the mean value computed from Moody’s data of recovery rates every class of industry and rating [10] . We assume that the recovery rate δ on all bonds is 30%. Furthermore, the recovery rate can also be determined by different methods such as Ordinary Least Squares (OLS) [17] , Multiple Additive Regression Trees (MART) [17] , Classification And Regression Trees (CART) [17] and Waterfall model [17] . These listed methods estimate the recovery rate in default by using their capital structure and some econometric factors at the time of default. Moody’s examined the determinants of recovery rates of defaulted corporate bonds and loans and proved that the recovery rates are strongly affected by many factors such as type of default event (e.g. Bankruptcy, failure to pay and restructuring), the tangibility of its assets, the amount of the debt and macroeconomic factors [18] .
Due to the difficulty of estimating the volatility σ and mean-reverting speed ? separately from market data of credit spread using only one bond issuer (or reference bond), we restrict ourselves to the limit distribution of the single factor CIR hazard rate-type model, and attempt to use the moment method to find those parameters. The moment method is a generic method or the most preferred numerical technique of estimating parameters in statistical model due to its less requirements of information.
5.2. Moment Method
Consider a set of observations of hazard rate![]() , which is obtained from historical market data calculated from the formula (13) (for a hazard rate of CIR type models) for a certain period of time. The market data can be collected daily or at the end of the month.
, which is obtained from historical market data calculated from the formula (13) (for a hazard rate of CIR type models) for a certain period of time. The market data can be collected daily or at the end of the month.
From the discussion about hazard rate models above, we recall that the elements of γ are the speed of mean reversion ?, the long mean rate b and the volatility σ.
In the case of the CIR model, CIR hazard rate ![]() has the following limits when
has the following limits when![]() ,
,
![]() (20)
(20)
where ![]() is a normal distribution. We assume that the relation (20) is satisfied in general for any value of t. In order to use the moment method technique, we consider as data the value of hazard rates
is a normal distribution. We assume that the relation (20) is satisfied in general for any value of t. In order to use the moment method technique, we consider as data the value of hazard rates ![]() at n points
at n points ![]() analogue as a vector
analogue as a vector
![]()
Obtained by historical market data calculated from the formula (13). Using the limit of expectation value of the hazard and substituting Equation (13) for the CIR model, we have
![]() (21)
(21)
Using the limit of variance and the definition formula of variance, and substituting Equation (13) for the CIR model, we have
![]()
We have, therefore,
![]() (22)
(22)
Having the estimator parameters δ and b, we have only to obtain the parameters values σ and ? which obey Equations (21) and (22) simultaneously. This may be done by solving, for example, the following system of two equations with two unknowns, ? and σ:
![]() (23)
(23)
Note that this system of equations in (23) is nonlinear equation. The solution of this system with ? and σ unknowns can be obtained by solving the systems of nonlinear simultaneous equations. (Typically, this is very difficult). Assume that
![]() (24)
(24)
This system of two nonlinear simultaneous equations can be solved on Matlab. This problem can also be formulated as the optimization problem i.e. we will seek to minimize ![]() and
and ![]() subject to
subject to![]() ,
,![]() .
.
This optimization problem is the problem of making the best possible choice of σ and ? that can minimize the objective function ![]() and
and ![]() simultaneously.
simultaneously.
Because of the rarity of data, we use 20 South Africa firm debts for maturity one year, three years and five years [16] . We use Matlab to find the solution to the system of non-linear Equations (24), with different initial guess values of ? and σ. These solutions are given in Table 1 for CIR hazard rate-type.
The results shown in Table 1 are the estimation of volatility σ and mean reversion ?, when hazard rates are distributed using a CIR model. Those are estimated by using various debt terms for 20 South African firms, with different rating from AAA to BBB and different market credit spreads for maturity in one year, three years, and five years. The result show that the mean reversion ? increases when volatility decreases, and decreases when volatility increases for firms from banking sector and non-banking sector. We notice that, the results are similar to those for the Vasicek-type model, and that the volatilities found are generally similar to volatilities of South African firm’s market data given in [16] .
6. Conclusions
In this paper, we have been concerned how the default is modeled for estimating the value of credit default swaps. We have considered the default model which takes the hazard rate as principal factor and distributed as the multi-factor Cox, Ingersoll and Ross (CIR) model, since it has some significant properties: mean reversion and affine. The explicit value of fixed side and recovery side of credit default swaps was determined in quite general form that contained counter party risk, under the multi-factor affine hazard rate. We suggested one implementation procedure when the available market data were not sufficiently rich and provided some simulation results. However, the work done in this paper has mainly been on the study of credit default swap under multi- factor hazard rate model, and the estimation of parameters associated with the single factor hazard rate model. These are done under the martingale measure or the original risk neutral measures. Moreover, as in real world the market is often incomplete, that is the existence of many martingale measures (or the risk neutral probability is not unique, refers to asset pricing theorem).
A natural extension of our estimation approach is to consider the calculation under the objective probability (or real world probability), investigate a case of correlation between a defaultable bond and the risk free interest rate (or correlation between the risk-free interest rate and all the hazard rates), and consider when defaultable bonds are issued by different firms.
Acknowledgements
The authors would like to acknowledge support of this work from Centre for Business Mathematics and Informatics and AIMS (African Institute for Mathematical Sciences). The work was done while Hopolang P. Mashele was a visiting researcher at AIMS.