Integral Representations for the Price of Vanilla Put Options on a Basket of Two-Dividend Paying Stocks ()
1. Introduction
An option is a contingent claim that presents its holder with the right, but not obligation, to purchase a given amount of underlying asset at some future date. In practice, the underlying asset is often the price of stock, commodity, foreign exchange rate, debit instrument, stock indices or future contract. Although the history of options extended back to several decades, it was not until 1973 that the trading of option was formalized by the establishment of the Chicago Board of Options of Exchange (CBOE). This same year was also a trading point for research in the valuation of financial derivatives.
Black and Scholes [1] published their seminar work on options valuation, in which they described a mathematical frame work for finding the fair price of a European option by means of a non-arbitrage argument to describe a second order partial differential equation which governed the evolution of the option price with respect to the time to expiry and the price of the underlying asset. Since then, there has been an explosive growth, both in the trading and the study of options of various kinds. Despite the success of the Black-Scholes model on hedging and pricing contingent claims, Merton [2] noted early that options quoted on the markets differed systematically from their predicted values, which led up to questioning the distributional assumptions based on geometric wiener process. European options are options that can be exercised only at the maturity date whereas American options can be exercised on or before the expiration date. The valuation of American options has received a lot of attention because most of options traded are of the American type. The early exercise premium of American options leads to a free boundary value problem under the framework of the Black and Scholes.
Basket option is defined as an option on a collection or basket of stocks. In other words, basket options are options whose payoff depends on the value of a basket, i.e., a portfolio of assets. Equity index options and currency basket options are classical examples of basket options. However, basket options are becoming increasingly widespread in commodity and particularly energy markets. The volatility of the basket is lower than the individual volatilities of the stocks and therefore these options are popular as hedging tools. The valuation of basket options is a challenging task because the underlying value is a weighted sum of individual asset prices. The common assumption of log-normality (and hence, the famous Black-Scholes formula) cannot be applied directly, because the sum of log-normal random variables is not log-normal. The valuation problem for American option on a basket of two-dividend paying stocks leads to the solution of a multi-dimensional free boundary problem.
Panini and Srivastav [3] considered option pricing with Mellin transforms. They derived the integral equation representations for the price of European and American basket put options with non-dividend yield using the Mellin transform techniques. Basket option pricing using Mellin transforms was considered by Manuge and Kim [4] . They used the Mellin transform to derive the analytical pricing formulas and Greeks for European and American basket put options.
For mathematical background, applications of the Mellin transforms and various numerical methods for the valuation of basket options (see [5] - [11] ) just mention a few.
In this paper, we apply double Mellin transform to derive integral representations for the prices of vanilla basket put options, namely, European and American basket put options with dividend yields. The rest of the paper is structured as follows. Section 2 presents the overview of the Black-Scholes partial differential equation for vanilla basket options of multi-dividend paying stocks. In Section 3, we apply the double Mellin transform method to derive the integral equations for the representations of the price of both European and American put options on a basket of two-dividend paying stocks. Section 4 concludes the paper.
2. Black-Scholes Partial Differential Equation for Vanilla Basket Options of Multi-Stocks with Dividend Yields
Consider the price of the underlying asset for the multi-stocks given by
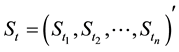(1)
Equation (1) is defined on the probability space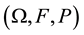 
and follows the geometric wiener process given by
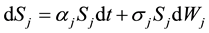(2)
where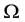 
is a sample space, 
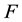is a set of events, 
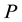is the probability measure, 
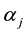is the drift parameter, 
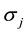is the volatility and 
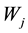is the Brownian motion.
The non-homogeneous Black-Scholes partial differential equation for vanilla options on a basket of multi- stocks with dividend yield is given by
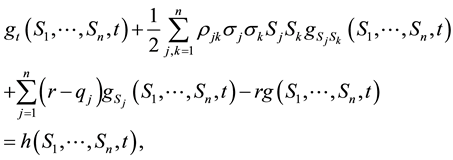(3)
Equation (3) can also be written as
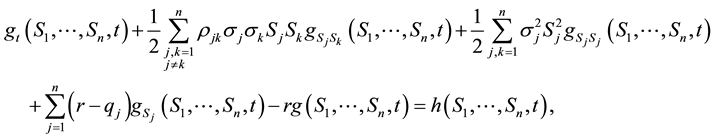(3a)
Suppose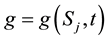 
is a multi-asset options with Lipschitz payoff function
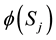. The boundary conditions imposed on (3) are reliant on the type of option (call or put). In general we let 
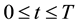and 
.
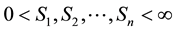Consider a vanilla put option; recall that when the option is granted exercise rights for any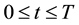
, the problem divides the price space into two regions. This early exercise boundary will depends on the payoff function of the option under consideration. The payoff function for a vanilla put option on a basket of multi-stocks is given by
![]()
(4)
Equation (4) is called the terminal condition for vanilla put option. For the put option, the continuation region
C exists for ![]()
and the exercise region E exists for![]()
. The smooth pasting condition can then
be stated as
![]()
(5)
When![]()
, the payoff in (4) becomes
![]()
(6)
Similar to the single asset option, the payoff function is equivalent to (4). As usual the option must satisfy the condition ![]()
in C. Due to the decomposition of American options, we can obtain the European option formula without directly solving for it. To utilize the Mellin transform method and the conditions that ensure its existence in [12] , we assume that ![]()
is bounded of polynomial degree when ![]()
and ![]()
i.e.
![]()
(7)
for any ![]()
on![]()
, where ![]()
is called fundamental strip. Equation (7) ensures the existence of the Mellin transform of ![]()
denoted by ![]()
The Mellin transform of ![]()
is defined as
![]()
(8)
By definition, the inversion formula for the Mellin transform of (8) is given by
![]()
(9)
where![]()
.
3. Integral Representations for the Price of Vanilla Put Options on a Basket of Two-Dividend Paying Stocks
This section presents the Mellin transform method for the valuation of European and American put options on a basket of two stocks with dividend yields.
3.1. Integral Representation for the Price of European Put Options on a Basket of Two-Dividend Paying Stocks
Setting![]()
, ![]()
for ![]()
in (4) and consider the homogeneous part of (4), we have the Black-Scholes partial differential equation for European put option on a basket of two stocks which pays dividend yield of the form
![]()
(10)
where ![]()
is called the price of European put option on a basket of two stocks ![]()
and![]()
.
The boundary conditions for (10) are given by
![]()
(11)
Now, we find an integral representation for the price of European put option ![]()
on a basket of two stocks ![]()
and ![]()
follow geometric wiener process with drift ![]()
and![]()
, volatilities ![]()
and ![]()
respectively. So, for![]()
, we have that
![]()
(12)
where the wiener processes ![]()
and ![]()
are Gaussian random variables with mean zero and variance ![]()
and![]()
.
Let ![]()
denotes the double Mellin transform of ![]()
defined as
![]()
(13)
Conversely, the inversion formula of (13) is given by
![]()
(14)
Taking the Mellin transform of (10), yields
![]()
(15)
where
![]()
(16)
Substituting (16) into (15), we have
![]()
(17)
Simplifying further, (17) becomes
![]()
(18)
Setting
![]()
(19)
Thus, (18) becomes
![]()
(20)
The general solution of (20) is called the complementary solution since it is homogeneous first order differential equation. The general solution is given by
![]()
(21)
where ![]()
is a constant of integration which is to be determined. Let us consider the terminal condition given by ![]()
in (11), then ![]()
can be obtained as
![]()
(22)
where ![]()
is the double Mellin transform of the terminal condition
![]()
. Therefore,
![]()
(23)
We introduce dimensionless variables
![]()
(24)
and using the localizing assumption that![]()
. Then
![]()
(25)
where![]()
.
Let
![]()
(25a)
Solving for the new domain gives![]()
. The determinant of the Jacobian matrix is
![]()
(25b)
Thus,
![]()
(25c)
Substituting (25a) and (25c) into (25), we have that
![]()
(25d)
From (24), for![]()
, we have that ![]()
. Hence (23) becomes
![]()
(26)
Using (22) and (26), then (21) yields
![]()
(27)
Substituting (27) into (14), we have that
![]()
(28)
Equation (28) is the integral representation of the price of European put option on a basket of two stocks with dividend yield via the double Mellin transform method.
3.2. Integral Representation for the Price of American Put Option on a Basket of Two-Dividend Paying Stocks
Now we consider the double Mellin transforms in order to derive the expression for the price of American put option on a basket of two stocks. American put option on a basket of two stocks gives the option’s holder the right to sell the basket stocks at any time from 0 to ![]()
and not only the expiration date![]()
.
The non-homogeneous Black-Scholes partial differential equation for American put option on a basket of two stocks with dividend yield is given by
![]()
(29)
where
![]()
(30)
The final time condition or terminal condition is given by
![]()
(31)
The other boundary conditions are given by
![]()
(32)
Let us assume that![]()
, then the free bounded condition is determined by the smooth pasting conditions given by
![]()
(33)
Using the same procedures of the double Mellin transform as for the case of European put option on a basket of two stocks with dividend yield. Let us denote the double Mellin transform for the price of American basket put option ![]()
as![]()
. The function ![]()
is the complex function of complex variable ![]()
which is defined as![]()
, ![]()
and can be expressed as
![]()
(34)
Conversely the inversion formula of the double Mellin transform is given by
![]()
(35)
Taking the Mellin transform of (29), we have that
![]()
(36)
where ![]()
is given by (19) and it has the same coefficient as that of its European put option counterpart. ![]()
is the Mellin transform of (30) which includes the free boundary as well. The general solution of (36) is given by
![]()
(37)
where ![]()
is the complementary solution of the homogeneous part and ![]()
is the particular solution of the nonhomogeneous part. Thus
![]()
(38)
where ![]()
is a constant of integration given by ![]()
Therefore,
![]()
(39)
Taking the double Mellin transform of (39) yields
![]()
(40)
Let us consider the nonhomogeneous part of (36) whose solution is given by
![]()
(41)
But
![]()
(42)
Setting
![]()
(42a)
So,
![]()
(43)
Solving (42a), we have respectively
![]()
(44)
![]()
(45)
![]()
(46)
Substituting (44), (45) and (46) into (43)
![]()
(47)
Substituting (47) into (41) yields
![]()
(48)
Taking the double Mellin transform of (48), we have that
![]()
(49)
The inverse double Mellin transform of (37) is given by
![]()
(50)
Substituting (40) and (49) into (50)
![]()
(51)
where ![]()
is the Beta function of ![]()
and![]()
.
Remarks
・ The integral equation for the price of European put option on a basket of two stocks with dividend yield can be obtained directly from the price of its counterpart, the American put option on a basket of two stocks. Hence, (51) can be written as
![]()
(52)
・ The second term in (51) is called early exercise premium.
・ For the case of non-dividend yield, (51) becomes
![]()
(53)
4. Conclusion
In this paper, we have considered vanilla basket put options, namely, European and American put options on a basket of two stocks with dividend yield. We used the integral method based on the double Mellin transform to derive the integral representations for the price of European and American put options on a basket of two-divi- dend paying stocks. We deduce from our results that by the decomposition of the price of American put option on a basket of two stocks, its counterpart “European put option” can be obtained directly as shown in (52).
NOTES
*Corresponding author.