Arbitrage-Free Gaussian Affine Term Structure Model with Observable Factors ()
1. Introduction
This paper analyzes a simple discrete-time affine multifactor model of the term structure of interest rates in which the factors of the model that follow a Gaussian first-order vector autoregression are observable and there are no possibilities for risk-free arbitrage. Rather than defining latent states indirectly through normalization on parameters governing the dynamics of latent states, a number of recent literatures have instead prescribed observable risk factors. For instance, [1] simply identified the factors with the yields themselves; [2] used both the yields and macroeconomic observables; [3] [4] and [5] used the first three principal components of yield curve. Our work positions itself in this line of research.
In the history of dynamic term structure model, the pricing factors are treated as shocks of various kinds that are not necessarily designed to be observable. Recent studies show that modeling the factors as observable has enormous computational advantages in the parameter estimation (“calibration”) process (see, for example, [3] [6] ). For arbitrage-free affine term structure model, the risk-neutral (hereafter denoted by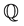 ) distribution parameters of pricing factors are directly related to the cross-section observations of the yield curve and we can use enough number of cross-section bond price observations at a given time (no less than that of
) distribution parameters of pricing factors are directly related to the cross-section observations of the yield curve and we can use enough number of cross-section bond price observations at a given time (no less than that of 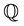 parameters) to identify the
parameters) to identify the 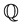 parameters at that time (in reality, it is common to use time series data and to assume fewer bond price observations at a given time than parameters). However, in order to estimate the behavior of the state factors under the real-world probability measure (hereafter denoted by
parameters at that time (in reality, it is common to use time series data and to assume fewer bond price observations at a given time than parameters). However, in order to estimate the behavior of the state factors under the real-world probability measure (hereafter denoted by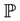 ), one generally must resort to time-series observations. In estimation, when the factors are observable, [3] showed that there is an inherent separation between the parameters of
), one generally must resort to time-series observations. In estimation, when the factors are observable, [3] showed that there is an inherent separation between the parameters of 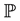 and
and 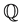 distributions of risk factors, which greatly facilitate the estimation of
distributions of risk factors, which greatly facilitate the estimation of 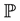 parameters. In contrast, when the risk factors are latent, estimates of the parameters governing the
parameters. In contrast, when the risk factors are latent, estimates of the parameters governing the 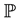 distribution necessarily depend on those of the
distribution necessarily depend on those of the 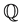 distribution of the state, since the pricing model is required to either invert the model for the fitted states (when some bonds are priced perfectly) or filter for the unobserved states (when all bonds are measured with errors).
distribution of the state, since the pricing model is required to either invert the model for the fitted states (when some bonds are priced perfectly) or filter for the unobserved states (when all bonds are measured with errors).
In this paper, although one of our goals is to classify a family of models that is convenient for empirical work, we are not directly concerned with estimation issues. We refer readers to the empirical studies for such issues, such as [3] [5] [6] and so on. We will restrict our attention to behavior under one particular equivalent martingale measure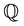 .
.
Contrary to traditional affine latent factor approach in which some dynamics for factors are assumed firstly and then establishing the factor loadings of yields through arbitrage-free restriction, we take the loadings on specific yields as given firstly and then parametrize the 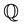 distribution of observable factors in a maximally flexible way consistent with no-arbitrage. That is, we specify the factor loadings exogenously, which is reasonable since the factors and yields are all observable.
distribution of observable factors in a maximally flexible way consistent with no-arbitrage. That is, we specify the factor loadings exogenously, which is reasonable since the factors and yields are all observable.
The remainder of this paper is structured as follows. In Section 2 we discuss the general Gaussian affine term structure models (GDTSM) and some assumptions imposed on yields and factors. In Section 3 we discuss the compatible dynamics of observable factors. In Section 4, we give an example. In Section 5, we conclude.
2. Gaussian Affine Term Structure Models
More precisely, for our purposes a useful starting point is the work by [3] , who show that every canonical GDTSM is observationally equivalent to the JSZ canonical GDTSM, and the discrete-time evolution of the risk factors (state vector) 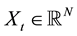 is governed by the following equations,
is governed by the following equations,
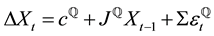 (1)
(1)
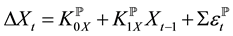 (2)
(2)
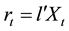 (3)
(3)
where 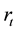 is the one-period spot interest rate, l is a column vector of ones,
is the one-period spot interest rate, l is a column vector of ones, ![]() is lower triangular (with positive diagonal),
is lower triangular (with positive diagonal), ![]() is in ordered real Jordan form,
is in ordered real Jordan form, ![]() , and
, and![]() ,
,![]() .
.
Here, we specify the Jordan form with each eigenvalue associated with a single Jordan block. Thus, when the eigenvalues ![]() are all real (see [3] for more general consideration),
are all real (see [3] for more general consideration), ![]() takes the form
takes the form![]() , where each
, where each
![]()
and where the blocks are in order of the eigenvalues.
Under Equations (1)-(3), the price of an n-year zero-coupon bond is given by
![]()
where ![]() and
and ![]() solve the first-order difference equations,
solve the first-order difference equations,
![]() (4)
(4)
![]() (5)
(5)
subject to the initial conditions![]() ,
, ![]() (see, for example, [7] ). The model-implied yield on a zero- coupon bond of maturity n is an affine function of the state
(see, for example, [7] ). The model-implied yield on a zero- coupon bond of maturity n is an affine function of the state![]() ,
,
![]() (6)
(6)
where ![]() and
and![]() .
.
In this setting, the factors are latent variables and the “loadings” (![]() and
and![]() ) are not specified a priori, but are derived from the no-arbitrage conditions and the calibration (e.g., via Kalman filtering) of the model.
) are not specified a priori, but are derived from the no-arbitrage conditions and the calibration (e.g., via Kalman filtering) of the model.
In other settings, the factor loadings may be specified a priori, for example, the dynamic Nelson-Siegel model
(DNS) was first proposed by [8] with ![]() and
and![]() , and then [9] derived cor-
, and then [9] derived cor-
responding Arbitrage-free model (AFNS) in which the absence of arbitrage and a priori specification of DNS loading actually restrict the coefficient of the process for the factors under ![]() measure to a certain form,
measure to a certain form,
![]() . [4] and [5] present a Principal-Component-Based Affine Term Structure Model in which the fac-
. [4] and [5] present a Principal-Component-Based Affine Term Structure Model in which the fac-
tors are the principal component of zero-coupon bond yields and the factor loadings for the corresponding bond yield are assigned a priori. They show in continuous-time frame that if the factors follow a mean-reverting dynamics, then the pre-specified factor loadings imposes some unexpected constraints on the reversion-speed ma- trix.
In the economy, we observe numerous zero-coupon bond yields with different maturities. We will take out from these yields a set of N yields, ![]() , as our key maturity yields for which (6) holds exactly. Collecting (6) into a vector system, we have
, as our key maturity yields for which (6) holds exactly. Collecting (6) into a vector system, we have
![]() (7)
(7)
where A an ![]() vector whose ith element is
vector whose ith element is ![]() and B an
and B an ![]() matrix whose ith row is
matrix whose ith row is![]() .
.
In this paper, we derive a discrete-time arbitrage-free Gaussian affine term structure model under the following assumptions:
Assumption 1: There are N observable factors Ft in real economy which can linearly span the latent factors Xt.
Assumption 2: The factors Ft loadings for our key maturity yields yt are known as a priori. The assumption 1 imply that we can express yt as the affine combinations of Ft.
![]() (8)
(8)
Assumption 2 means that u and U are given exogenously.
In the following, we define the process of ![]() under risk-neutral measure
under risk-neutral measure ![]() as,
as,
![]() (9)
(9)
where ![]() is a column vector of length N and
is a column vector of length N and ![]() is the coefficient matrix for Ft. Because Ft is observable,
is the coefficient matrix for Ft. Because Ft is observable, ![]() need not be normalized (contrary to the situation of latent factors) and could be any form of
need not be normalized (contrary to the situation of latent factors) and could be any form of ![]() matrix.
matrix.
And the risk-free rate can be expressed as the affine functions of the vector of observable factors Ft. Without loss of generality we can define
![]() (10)
(10)
where ![]() is a scalar and
is a scalar and ![]() is a column vector of length N.
is a column vector of length N.
3. The Compatible Dynamics of Observable Factors
In the following, we will take u and U as given exogenously and find compatible dynamics of observable factors. We first derive restrictions on parameters of the process of observable factors Ft under risk-neutral measure ![]() and then derive restriction on parameters of risk-free rate Equation (10).
and then derive restriction on parameters of risk-free rate Equation (10).
3.1. Restrictions on Risk-Neutral Parameters of Factor Process-![]() and
and ![]()
Theorem 1. Given key maturities![]() , an invertible loadings matrix
, an invertible loadings matrix ![]() and an arbitrary choice of N real eigenvalues
and an arbitrary choice of N real eigenvalues ![]() of the coefficient matrix
of the coefficient matrix![]() , then the full
, then the full ![]() is given by
is given by
![]() (11)
(11)
where ![]() is a Jordan matrix with m blocks, such that any identical eigenvalues reside in the same Jordan block. Matrix G is given as follows:
is a Jordan matrix with m blocks, such that any identical eigenvalues reside in the same Jordan block. Matrix G is given as follows:
![]() (12)
(12)
where ![]() are distinct eigenvalues of multiples
are distinct eigenvalues of multiples![]() , such that
, such that![]() . Functions
. Functions ![]() is defined as
is defined as
![]()
with ![]() and
and ![]() being
being
![]()
![]()
Proof:
Combining Equations (8) and (7), we have,
![]() (13)
(13)
Substituting Equation (13) into Equation (1), we have,
![]() (14)
(14)
We will call Equation (14) the model consistency condition.
From Equations (4) and (6), we observe that
![]() (15)
(15)
According to [4] , for any Jordan canonical form![]() , the function
, the function ![]() can be
can be
defined as![]() , where
, where ![]() is function f of the Jordan block
is function f of the Jordan block![]() , defined as
, defined as
![]()
Applying this formula to Equation (15), we have![]() , where we define
, where we define![]() . Defining
. Defining ![]() and calculating it by direct matrix manipulation, we have
and calculating it by direct matrix manipulation, we have
![]() (15*)
(15*)
where,
![]()
![]()
Defining![]() , then we have,
, then we have,
![]()
where ![]() is a row vector of length
is a row vector of length ![]() such that
such that![]() . Therefore, we can rewrite
. Therefore, we can rewrite ![]() as
as
![]() (16)
(16)
Let us define a block diagonal matrix
![]() (17)
(17)
where ![]() is given by
is given by
![]()
Now let
![]() (18)
(18)
where ![]() is a row vector of length
is a row vector of length![]() . We have:
. We have:
![]()
That is
![]() (19)
(19)
Substituting Equations (17), (18) and (19) into Equation (16), we have
![]() (20)
(20)
From Equation (14), we have
![]() (21)
(21)
In deriving Equation (21), we use
![]()
We can check the relation ![]() by direct matrix multiplication.
by direct matrix multiplication.
n
Thus by construction we have shown that with U given, ![]() is always unique for a given choice of eignvalues and key maturities, which is the same as the conclusion of [4] .
is always unique for a given choice of eignvalues and key maturities, which is the same as the conclusion of [4] .
Since we assume the factors Ft are observable and the covariance matrix ![]() for Ft under the
for Ft under the ![]() measure are the same as that under the
measure are the same as that under the ![]() measure, we can use the real data for Ft to calculate
measure, we can use the real data for Ft to calculate![]() . Thus, without loss of generality, we assume
. Thus, without loss of generality, we assume ![]() to be known a priori. Under this assumption, we give the following theorem.
to be known a priori. Under this assumption, we give the following theorem.
Theorem 2. Given the choice of key maturities![]() , an invertible loadings matrix
, an invertible loadings matrix![]() , an intercept loading vector u, a covariance matrix for the observable factors
, an intercept loading vector u, a covariance matrix for the observable factors ![]() and an arbitrary choice of N real eigenvalues
and an arbitrary choice of N real eigenvalues ![]() of the coefficient matrix
of the coefficient matrix![]() , the intercept vector
, the intercept vector ![]() can be determined only by a free scalar parameter
can be determined only by a free scalar parameter![]() , that is
, that is
![]() (22)
(22)
where ![]() is the first column vector of G,
is the first column vector of G, ![]() and
and![]() , with
, with
![]()
![]()
Proof:
From Equations (14), (20) and (21), we have
![]() (23)
(23)
In addition,
![]()
where ![]() is defined as that in Equation (12). We define
is defined as that in Equation (12). We define ![]()
which is the first column of matrix G, and then we have![]() .
.
From Equations (5) and (6), we have
![]()
where
![]()
![]()
Then,
![]()
Calculating the summation in the above equation, we get
![]()
We define![]() , and then we have
, and then we have
![]() (24)
(24)
where ![]() and
and![]() . From Equation (22), we have
. From Equation (22), we have
![]()
n
3.2. Restrictions on Parameters of Risk-Free Rate Equation-![]() and
and ![]()
Theorem 3. Vector ![]() in Equation (10) is uniquely determined by the choice of key maturities
in Equation (10) is uniquely determined by the choice of key maturities![]() , an invertible loadings matrix
, an invertible loadings matrix ![]() and an arbitrary choice of N real eigenvalues
and an arbitrary choice of N real eigenvalues ![]() of the coefficient matrix
of the coefficient matrix![]() . Thus the loadings of the risk-free rate on the factors are fixed by such choice.
. Thus the loadings of the risk-free rate on the factors are fixed by such choice.
![]() (25)
(25)
where G is defined by Equation (12) and ![]() is a unit row vector
is a unit row vector ![]() of length
of length![]() , equal to the dimension of the Jordan block
, equal to the dimension of the Jordan block![]() .
.
Proof:
Substituting Equation (13) into Equation (3), we have,
![]() (26)
(26)
From Equation (20), we have
![]() (27)
(27)
For![]() , we have
, we have![]() , where
, where ![]() has the following form,
has the following form,
![]()
As before, let ![]() be a row vector of length
be a row vector of length ![]() such that
such that![]() , then we have
, then we have
![]()
Since![]() , we have
, we have
![]() . (28)
. (28)
Substituting Equation (28) into Equation (27), we get![]() .
.
n
Theorem 4. Let parameters of the model, ![]() ,
, ![]() , u,
, u, ![]() and
and ![]() be given, then
be given, then ![]() is fixed accordingly. The expression for
is fixed accordingly. The expression for ![]() is as follows
is as follows
![]() (29)
(29)
where G and ![]() are defined as Equation (25),
are defined as Equation (25), ![]() and
and ![]() are defined as Equation (22).
are defined as Equation (22).
Proof:
From Equations (26) and (28), we have
![]() (30)
(30)
Substituting Equation (24) into Equation (30), we get
![]()
n
4. Example
Consider a 3-dimensional observable affine factor model, and let the eigenvalues of the coefficient matrix ![]() be
be ![]() and
and![]() . Then the full matrix is given by
. Then the full matrix is given by
![]()
![]()
![]()
![]() ,
,
where
![]()
![]()
![]()
![]()
![]()
![]()
From Equations (15) and (15*), we have the close form for![]() ,
,
![]()
5. Conclusions
A number of previous researchers have discussed the affine term structure with the pricing factors being observable. A distinctive feature of the models with observable factors is its computational advantage over that with latent factors. However, these researches just focus on the computational convenience but do not study such model in depth.
In this paper, our results show that if we treat the pricing factors observable and thus the factors loadings of some key maturity yields are given a priori, the no-arbitrage condition will impose strict restrictions on the risk-neutral dynamics of the observable factors and on the parameters of risk-free rate equation.
We discuss how to impose some important constraints on the ![]() dynamics of the factors when we assume the factors are observable and there are no possibilities for risk-free arbitrage. Our results suggest that, given key maturities and an invertible factor loadings matrix, the coefficient matrixes under risk-neutral measure are fixed by an arbitrary choice of N real eigenvalues
dynamics of the factors when we assume the factors are observable and there are no possibilities for risk-free arbitrage. Our results suggest that, given key maturities and an invertible factor loadings matrix, the coefficient matrixes under risk-neutral measure are fixed by an arbitrary choice of N real eigenvalues ![]() and that the
and that the ![]() intercept parameters of the factor dynamics and the parameters governing the risk-free rate equation are also determined by these N real eigenvalues in addition to a free scalar
intercept parameters of the factor dynamics and the parameters governing the risk-free rate equation are also determined by these N real eigenvalues in addition to a free scalar![]() .
.
Acknowledgements
This work is supported by Research Innovation Foundation of Shanghai University of Finance and Economics under Grant No. CXJJ-2013-321. And I am grateful for helpful comments from the anonymous referee and especially to Professor Hong Li for his support and encouragement. All errors are my own.