1. Introduction
Around 1945, Alfred Tarski proposed several questions concerning the elementary theory of non-abelian free groups. These questions then became well-known conjectures but remained open for 60 years. They were proved in the period 1996-2006 independently by O. Kharlampovich and A. Myasnikov [1] -[5] , and by Z. Sela [6] -[10] . The proofs, by both sets of authors, were monumental, and involved the development of several new areas of infinite group theory. Because of the tremendous amount of material developed and used in the two different proofs, the details of the solution are largely unknown, even to the general group theory population. The book [11] presents an introductory guide through the material. In this paper we provide, for a general mathematical audience, who know some infinite group theory, an introduction to both the Tarksi conjectures and the vast new ideas that go into the proof. These ideas straddle the line between algebra and mathematical logic and hence most group theorists don’t know enough logic to fully understand the details while in the other direction most logicians don’t understand enough infinite group theory.
In the next section we define and explain both elementary and universal theory. With these in hand we can explain precisely the Tarski problems and what has been actually proved. We then in section 4 discuss the history of the solution as well as the components of the proof. This involves the development of several new areas of infinite group theory.
There are five essential parts of the overall proof: the structure theory of fully residually free groups, called limit groups in the Sela approach; the Makhanin-Razborov techniques for handling solutions of equations in free groups; the extension of classical algebraic geometry to algebraic geometry over groups, especially over free groups. Sela calls this diophantine geometry over groups, an elimination process that reduces the solution of systems of equations over free groups to solutions of certain special systems of quadratic equations, and an implicit function theorem that allows for quantifer elimination and then an induction on the number of quantifiers.
We then provide the basic strategy for the proof which utilizes all the components mentioned. In section 6 we give a very brief outline of the proof.
As part of the proof both sets of authors provide a complete characterization of finitely generated groups that have the same elementary theory as the class of non-abelian free groups. These are called elementary free or elementarily free groups. In the approach of Kharlampovich-Myasnikov these are called special NTQ-groups while Sela calls them w-residually free towers. The most prominent set of examples of non-free elementary free groups are the orientable surface groups 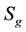 of genus
of genus 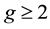 and the non-orientable surface groups
and the non-orientable surface groups 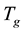 of genus
of genus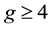 . In the final section, we finish this paper with a discussion of elementary free groups and what we call something for nothing results.
. In the final section, we finish this paper with a discussion of elementary free groups and what we call something for nothing results.
2. Elementary and Universal Theory
The original Tarski Problems or Tarski Conjectures asked, among other things, whether all non-abelian free groups satisfy the same first-order or elementary theory. Here we explain and review universal and elementary theory.
A first-order sentence in group theory has logical symbols 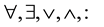 but no quantification over sets. A first-order theorem in a free group is a theorem that says a first-order sentence is true in all non-abelian free groups. We make this a bit more precise:
but no quantification over sets. A first-order theorem in a free group is a theorem that says a first-order sentence is true in all non-abelian free groups. We make this a bit more precise:
We start with a first-order language appropriate for group theory. This language, which we denote by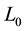 , is the first-order language with equality containing a binary operation symbol. a unary operation symbol−1 and a
, is the first-order language with equality containing a binary operation symbol. a unary operation symbol−1 and a
constant symbol 1. A universal sentence of 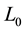 is one of the form
is one of the form 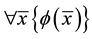 where
where 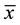 is a tuple of distinct
is a tuple of distinct
variables, 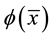 is a formula of
is a formula of 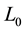 containing no quantifiers and containing at most the variables of
containing no quantifiers and containing at most the variables of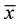 .
.
Similarly an existential sentence is one of the form 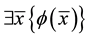 where
where 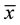 and
and 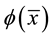 are as above. A
are as above. A
universal-existential sentence is one of the form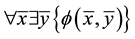 . Similarly defined is an
. Similarly defined is an ![]()
existential-universal sentence. It is known that every sentence of ![]() is logically equivalent to one of the form
is logically equivalent to one of the form
where ![]() is a tuple of distinct variables, each
is a tuple of distinct variables, each ![]() for
for ![]() is a quantifier, either
is a quantifier, either ![]() or
or![]() ,
,
and ![]() is a formula of
is a formula of ![]() containing no quantifiers and containing free at most the variables
containing no quantifiers and containing free at most the variables![]() . Further vacuous quantifications are permitted. Finally a positive sentence is one logically equivalent to a sentence constructed using (at most) the connectives
. Further vacuous quantifications are permitted. Finally a positive sentence is one logically equivalent to a sentence constructed using (at most) the connectives![]() .
.
If G is a group, then the universal theory of G consists of the set of all universal sentences of ![]() true in G. We denote the universal theory of a group G by
true in G. We denote the universal theory of a group G by![]() . Since any universal sentence is equivalent to the negation of an existential sentence it follows that two groups have the same universal theory if and only if they have the same existential theory. We say that two group G, H are universally equivalent if
. Since any universal sentence is equivalent to the negation of an existential sentence it follows that two groups have the same universal theory if and only if they have the same existential theory. We say that two group G, H are universally equivalent if
![]() .
.
The set of all sentences of ![]() true in G is called the first-order theory or the elementary theory of G. We denote this by
true in G is called the first-order theory or the elementary theory of G. We denote this by![]() . We note that being first-order or elementary means that in the intended interpretation of any formula or sentence all of the variables (free or bound) are assumed to take on as values only individual group elements―never, for example, subsets of nor functions, on the group in which they are interpreted.
. We note that being first-order or elementary means that in the intended interpretation of any formula or sentence all of the variables (free or bound) are assumed to take on as values only individual group elements―never, for example, subsets of nor functions, on the group in which they are interpreted.
We say that two groups G and H are elementarily equivalent (symbolically![]() ) if they have the
) if they have the
same first-order theory, that is![]() .
.
Group monomorphisms which preserve the truth of first-order formulas are called elementary embeddings. Specifically, if H and G are groups and
![]()
is a monomorphism then ![]() is an elementary embedding provided whenever
is an elementary embedding provided whenever ![]() is a formula of
is a formula of
![]() containing free at most the distinct variables
containing free at most the distinct variables ![]() and
and ![]() then
then ![]() is true
is true
In H if and only if
![]()
is true in G. If H is a subgroup of G and the inclusion map ![]() is an elementary embedding then we say that G is an elementary extension of H.
is an elementary embedding then we say that G is an elementary extension of H.
Two very important concepts in the elementary theory of groups, are completeness and decidability. Given a non-empty class of groups ![]() closed under isomorphism then we say its first-order theory is complete if given a sentence
closed under isomorphism then we say its first-order theory is complete if given a sentence ![]() of
of ![]() then either
then either ![]() is true in every group in
is true in every group in ![]() or
or ![]() is false in every group in
is false in every group in![]() . The first-order theory of
. The first-order theory of ![]() is decidable if there exists a recursive algorithm which, given a sentence
is decidable if there exists a recursive algorithm which, given a sentence ![]() of
of ![]() decides whether or not
decides whether or not ![]() is true in every group in
is true in every group in![]() .
.
For more information on elementary theory in general see [11] -[13] .
3. The Tarski Problems
Tarski first asked the general question whether all non-abelian free groups share the same elementary theory. At the end of this section, we will present some motivation for this idea. Vaught, a student of Tarksi’s, proved almost immediately that all free groups of infinite rank do have the same elementary theory, and thus reduced the question to the class of non-abelian free groups of finite rank. After this, Tarski’s question was formalized into the following conjectures.
Tarski Conjecture 1 Any two non-abelian free groups are elementarily equivalent. That is any two non- abelian free groups satisfy exactly the same first-order theory.
Tarski Conjecture 2 If the non-abelian free group H is a free factor in the free group G then the inclusion map ![]() is an elementary embedding.
is an elementary embedding.
The second conjecture is stronger than the first and in fact implies the first. If true, then the theory of the non-abelian free groups would be complete, that is given a sentence ![]() of
of ![]() then either
then either ![]() is true in every non-abelian free group or
is true in every non-abelian free group or ![]() is false in every non-abelian free group.
is false in every non-abelian free group.
After a long series of partial results, that we will describe in subsequent sections, the positive solution to the Tarksi conjectures was given by O. Kharlampovich and A. Myasnikov [1] -[5] and independently by Z. Sela [6] - [10] . The proofs by both sets of authors involved the development of whole new areas of mathematics, in particular an algebraic geometry (Sela calls this diophantimne geometry) over free groups. The basic theorems eventually proved were:
Theorem 1 (Tarski 1) Any two non-abelian free groups are elementarily equivalent. That is any two non- abelian free groups satisfy exactly the same first-order theory.
Theorem 2 (Tarski 2) If the non-abelian free group H is a free factor in the free group G then the inclusion map ![]() is an elementary embedding.
is an elementary embedding.
In addition to the completeness of the theory of the non-abelian free groups, the question of its decidability also arises. The decidability of the theory of non-abelian free groups means the question of whether there exists a recursive algorithm which, given a sentence ![]() of
of![]() , decides whether or not
, decides whether or not ![]() is true in every non- abelian free group. Kharlampovich and Myasnikov in addittion to the proofs of the main Tarksi conjectures also proved that the theory is decidable (see [5] )
is true in every non- abelian free group. Kharlampovich and Myasnikov in addittion to the proofs of the main Tarksi conjectures also proved that the theory is decidable (see [5] )
Theorem 3 (Tarski 3) The elementary theory of the non-abelian free groups is decidable.
Although Tarksi was never explicit on the origin of the basic question, it is motivated by several basic results, and concepts, in the theory of free groups (see [11] [14] [15] for complete discussions of free groups). First is the observation that most free group properties, involving elements, are rank independent, that is, true for all free groups independent of rank. For example all non-abelian free groups are torsion-free and all abelian subgroups of non-abelian free groups are cyclic.
A second possible motivation, which also shows that all non-abelian free groups have the same universal theory, is the following. Let ![]() be a free group of rank 2. It is a straightforward consequence of the Reide- meister-Schreier process (see [14] ) that the commutator subgroup of
be a free group of rank 2. It is a straightforward consequence of the Reide- meister-Schreier process (see [14] ) that the commutator subgroup of ![]() is free of infinite rank. This implies that if we let
is free of infinite rank. This implies that if we let ![]() denote a free group of countably infinite rank, then
denote a free group of countably infinite rank, then![]() . It follows that for any
. It follows that for any ![]() with
with ![]() we have
we have
![]()
This shows that ![]() and
and![]() . Its like a snake eating its tail.
. Its like a snake eating its tail.
If ![]() then any universal sentence in H must also be true in G, that is
then any universal sentence in H must also be true in G, that is![]() . This obser-
. This obser-
vation combined with the observations above prove that all non-abelian free groups have the same universal theory and hence are universally equivalent.
Theorem 4 All non-abelian free groups are universally equivalent.
A group with the same universal theory as a non-abelian free group is called a universally free group. The above theorem then opens the question as to whether the class of universally free groups extends beyond the class of free groups. One of the initial steps toward the proof of the Tarksi problems was a group theoretical characterization of universally free groups. In the finitely generated case these turn out to be the non-abelian fully residually free groups. We will introduce this class of groups in the next section.
4. The History of the Solution
The final proof of the Tarski theorems was a monumental collection of work by both sets of authors. In addition to dealing with already existing ideas in group theory and logic, the solution involved the development of several new areas of group theory. In particular three areas of group theory had to be fully developed before the proof could be completed. These were:
1) The theory of fully residually free groups. In Sela’s approach these were called limit groups;
2) The Makhanin-Razborov technique for solving equations within free groups;
3) The development of algebraic geometry over groups. Sela calls this diophantine geometry.
We will discuss each of these in turn. First we look at the initial partial results that were done between the statement of the problem by Tarksi (in 1945) and the final proofs (1998-2006).
The first progress was due to Vaught, a student of Tarski, who showed that the Tarski Conjectures 1, 2 are true if G and H are both free groups of infinite rank. This reduced the problem to free groups of finite rank, that is, in showing that all non-abelian free groups of finite rank share the same elementary theory or even stronger that the embedding of a free group of rank m into a free group of rank n, with![]() , is an elementary embedding.
, is an elementary embedding.
The basic idea in Vaught’s proof is to use the following criteria for elementary embeddings; if ![]() is a
is a
subgroup of H and that to every finite subset ![]() of
of ![]() and every element
and every element ![]() there exists an
there exists an
automorphism ![]() of H fixing
of H fixing ![]() and mapping b into
and mapping b into![]() , then the inclusion map from
, then the inclusion map from ![]() into H is an elementary embedding. Applying this criterion to free groups of infinite rank, suppose that F is free on an infinite subset S and that G is free on an infinite subset
into H is an elementary embedding. Applying this criterion to free groups of infinite rank, suppose that F is free on an infinite subset S and that G is free on an infinite subset ![]() of S. Then permutations of S will induce enough automorphisms to guarantee that the inclusion map of G into F is an elementary embedding.
of S. Then permutations of S will induce enough automorphisms to guarantee that the inclusion map of G into F is an elementary embedding.
The next significant progress was due to Merzljakov [16] . A positive sentence is a first-order sentence which is logically equivalent to a sentence constructed using (at most) the connectives![]() . The positive theory of a group G consists of all the positive sentences true in G.
. The positive theory of a group G consists of all the positive sentences true in G.
Merzljakov showed that the non-abelian free groups have the same positive theory.
Theorem 5 (Merzljakov) [16] All non-abelian free groups have the same positive theory.
Merzljakov’s proof used what are now called generalized equations and a quantifier elimination process. This was a precursor to the methods used in the eventual solution of the overall Tarksi problems.
As we pointed out in the previous section, two non-abelian free groups satisfy the same universal theory. Sacerdote [17] proved that this could be extended to universal-existential sentences. The set of universal- existential sentences true in a group G is called the ![]() -theory of G. Hence Sacredote’s result is then:
-theory of G. Hence Sacredote’s result is then:
Theorem 6 (Sacerdote) [17] All non-abelian free groups have the same ![]() -theory.
-theory.
That all non-abelian free groups have the same universal theory coupled with the fact that universally free is equivalent to existentially free says that Tarski Conjecture 1 is true if there is only one quantifier. Sacerdote’s extension to ![]() -theory shows that the Tarski Conjecture 1 is true if there are two quantifers. Sacerdote’s theorem becomes the initial step in the final proof which employs an induction based on the number of quantifiers.
-theory shows that the Tarski Conjecture 1 is true if there are two quantifers. Sacerdote’s theorem becomes the initial step in the final proof which employs an induction based on the number of quantifiers.
A first step to the initial proofs was to completely characterize those groups that are universally free. This was accomplished within the study of fully residually free groups. A group G is residually free if for each non- trivial ![]() there is a homomorphism
there is a homomorphism ![]() where F is a free group and
where F is a free group and![]() .
.
A group G is fully residually free if for each finite subset of non-trivial elements ![]() in G there
in G there
is a homomorphism ![]() where F is a free group and
where F is a free group and ![]() for all
for all![]() .
.
Fully residually free groups arise in Sela’s approach as limiting groups of homomorphisms from a group G into a free groups. Sela shows that such groups in the finitely generated case are equivalent to fully residually free groups. Hence. a finitely generated fully residually free group is also called a limit group. This has become the more common designation.
Two concepts are crucial in the study of limit groups. A group G is commutative transitive or CT if commutativity is transitive on the set of non-trivial elements of G. That is if ![]() and
and ![]() for non-trivial elements
for non-trivial elements ![]() then
then![]() . A group G is CSA or conjugately separated abelian if
. A group G is CSA or conjugately separated abelian if
maximal abelian subgroups are malnormal. A subgroup ![]() is malnormal if
is malnormal if ![]() implies
implies
that![]() . CSA groups are always CT but there exist CT groups that are not CSA. As we will see, in the presence of residual freeness they are equivalent. A classification of CT non-CSA groups was given by Fine, Gaglione, Rosenberger and Spellman (see [11] )
. CSA groups are always CT but there exist CT groups that are not CSA. As we will see, in the presence of residual freeness they are equivalent. A classification of CT non-CSA groups was given by Fine, Gaglione, Rosenberger and Spellman (see [11] )
In 1967 Benjamin Baumslag [18] proved the following result who’s innocuous beginnings belied its much greater later importance. It was in this paper that the concept of full residual freeness was first explored.
Theorem 7 (Baumslag [18] ) Suppose G is residually free. Then the following are equivalent:
1) G is fully residually free;
2) G is commutative transitive.
Gaglione and Spellman [19] and independently Remeslennikov [20] extended B. Baumslag’s Theorem and this extension became one of the cornerstones of the proof of the Tarksi problems
Theorem 8 [19] [20] Suppose G is residually free. Then the following are equivalent:
1) G is fully residually free;
2) G is commutative transitive;
3) G is universally free if non-abelian.
Further the result can be extended to include the equivalence with CSA. In addition Remeslennikov and independently Chiswell (see [21] ) showed that if a group G is finitely generated then being fully residually free is equivalent to being universally free. Therefore the finitely generated universally free groups are precisely the finitely generated fully residually free groups which are non-abelian
Theorem 9 Let G be finitely generated and non-abelian. Then G is a limit group if and only if G is uni- versally free.
Ciobanu, Fine and Rosenberger [22] recently greatly extended the class of groups satisfying both B. Baumslag’s original theorem and the theorem of Gaglione, Spellman and Remeslennikov.
The solution of the Tarski Conjectures involved analyzing groups which have the same elementary theory as a free group. Clearly this includes the universally free groups and therefore the theory of limit groups became essential to the proof and to analyzing those groups which have the same elementary theory as a free group
It was clear from the beginning that to deal with the Tarski problems it was necessary to give a precise definition of solution sets of equations and inequations over free groups. In this direction Lyndon [23] introduced the concept of an exponential group, that is a group which allows parametric exponents in an associative unitary ring A. In particular he studied the free exponential group ![]() where exponents are allowed from the polynomial ring
where exponents are allowed from the polynomial ring ![]() over the integers
over the integers![]() . Lyndon established that the free exponential group
. Lyndon established that the free exponential group ![]() and hence any finitely generated subgroup of it, is fully residually free and hence, if it is non-abelian, universally free. Kharlampovich and Myasnikov [1] [2] established the converse; therefore a finitely generated group is fully residually free if and only if it is embeddable in
and hence any finitely generated subgroup of it, is fully residually free and hence, if it is non-abelian, universally free. Kharlampovich and Myasnikov [1] [2] established the converse; therefore a finitely generated group is fully residually free if and only if it is embeddable in![]() .
.
Lyndon’s original motivation for introducing exponential groups was from the solution sets of equations over free groups. In [23] he found that the solution set of any equation with one variable over a free group F can be obtained from finitely many parametric words by specializing their parameters in the integers. A parametric
word with parameters in ![]() is a formal expression obtained from a basis for F by finitely many
is a formal expression obtained from a basis for F by finitely many
concatenations and exponentiations from![]() . If one specializes the parameters
. If one specializes the parameters ![]() in
in ![]() one
one
obtains an element of F. Lyndon proved that for any equation with one variable over a free group ![]() one can
one can
effectively find a finite set of parametric words with parameters from the ring ![]() such that any
such that any
solution of this equation can be obtained from some specialization of these words. Appel [34] refined Lyndon’s result and showed that the solution set of a one variable equation over a free group can be
parametrized by a finite set of words of the form ![]() where
where ![]() and
and![]() .
.
A further detailed study of the structure of exponential groups was carried out by A. Myasnikov and V. Remeslennikov (see [11] ). They proved that the group ![]() can be obtained starting from F by an infinite chain of a special type of HNN extensions called extensions of centralizers. If G is a group and G is the centralizer of a non-trivial element in G then
can be obtained starting from F by an infinite chain of a special type of HNN extensions called extensions of centralizers. If G is a group and G is the centralizer of a non-trivial element in G then
![]()
is a free extension of the centralizer C by s. From the work of Myasnikov and Remeslennikov, to construct![]() , one needs to extend each centralizer sufficiently many times so that every proper centralizer is isomorphic to a free abelian group of infinite rank―the additive group of
, one needs to extend each centralizer sufficiently many times so that every proper centralizer is isomorphic to a free abelian group of infinite rank―the additive group of![]() . This further implies that any finitely generated subgroup of
. This further implies that any finitely generated subgroup of ![]() and hence any fully residually free group, is actually a subgroup of a group that can be obtained from F by finitely many extensions of centralizers. For such groups, Bass-Serre theory (see [11] ) can be used to determine the structure. Kharlampovich and Myasnikov proved a finitely generated group is fully residually free if and only if it is embeddable in the free exponential group
and hence any fully residually free group, is actually a subgroup of a group that can be obtained from F by finitely many extensions of centralizers. For such groups, Bass-Serre theory (see [11] ) can be used to determine the structure. Kharlampovich and Myasnikov proved a finitely generated group is fully residually free if and only if it is embeddable in the free exponential group ![]() introduced by Lyndon.
introduced by Lyndon.
Advances in a different direction were given by Makanin and Razborov (see [24] -[26] ). Makanin proved that there exists an algorithm to determine, given a finite system of equations over a free group, whether the system possesses at least one solution. Razborov working with the Makanin algorithm determined an algorithm to effectively describe the solution sets of a finite system of equations over a free group.
Kharlampovich and Myasnikov further refined the Makanin-Razborov method. Their technique allows one to transform arbitrary finite systems of equations in free groups to some canonical forms and describe precisely the irreducible components of algebraic sets in free groups.
These canonical forms consist of finitely many quadratic equations in a triangular form. The following result is a corollary of the decidability of the Diophantine problem
Theorem 10 (Makanin) [24] [25]
1) The existential (and hence the universal) theory of a free group is decidable;
2) The positive theory of a free group is decidable.
The final ingredient that was needed for the proof was the development of an algebraic geometry over groups. In analogy with the classical theory of equations over number fields, algebraic geometry over groups was developed by Baumslag, Myasnikov and Remeslennikov [27] [28] . The theory of algebraic geometry over groups translated the basic notions of the classical algebraic geometry: algebraic sets, the Zariski topology, Noetherian domains, irreducible varieties, radicals and coordinate groups to the setting of equations over groups.
This provided the necessary machinery to transcribe important geometric ideas into pure group theory. The proof of the Tarski Conjectures depends on the algebraic geometry of free groups. In particular it depends on the description of a fully residually free group as the coordinate group of an irreducible algebraic variety. We review some of the basic definitions from the algebraic geometry over groups. These mirror for the most part the standard definitions in classicial algebraic geometry.
Let G be a group generated by a finite set![]() ,
, ![]() be a free group with basis
be a free group with basis![]() , and let
, and let ![]() be the free product of G and
be the free product of G and![]() . A system of equations over
. A system of equations over ![]() is an expression
is an expression ![]() where
where![]() . As an element of the free product, the left side of every equation in
. As an element of the free product, the left side of every equation in ![]()
can be written as a product of some elements from the basis ![]() and their inverses and some
and their inverses and some
elements from![]() . The elements from
. The elements from ![]() are called variables while the elements from
are called variables while the elements from ![]() are called constants. To emphasize this we sometimes write
are called constants. To emphasize this we sometimes write ![]() as
as ![]() or just
or just![]() .
.
A solution of the system ![]() over a group G is a tuple of elements
over a group G is a tuple of elements ![]() such that after replacing each
such that after replacing each ![]() by
by ![]() the left hand side of every equation in
the left hand side of every equation in ![]() becomes the trivial element of G. Equivalently, a solution of the system
becomes the trivial element of G. Equivalently, a solution of the system ![]() over G can be described as a G-homomorphism
over G can be described as a G-homomorphism ![]()
such that![]() . Denote by
. Denote by ![]() the normal closure of S in
the normal closure of S in![]() , and by GS the quotient group
, and by GS the quotient group
![]() . Then every solution of
. Then every solution of ![]() in G gives rise to a G-homomorphism
in G gives rise to a G-homomorphism ![]() and vice
and vice
versa. By ![]() we denote the set of all solutions in G of the system
we denote the set of all solutions in G of the system![]() , it is called the algebraic set defined by S. This algebraic set
, it is called the algebraic set defined by S. This algebraic set ![]() uniquely corresponds to the normal subgroup
uniquely corresponds to the normal subgroup
![]()
of the group![]() . Notice that if
. Notice that if![]() , then
, then![]() . The subgroup
. The subgroup ![]() contains S, and it
contains S, and it
is called the radical of S, denoted by![]() . The quotient group
. The quotient group
![]()
is the coordinate group of the algebraic set![]() . Again, every solution of
. Again, every solution of ![]() in G can be
in G can be
described as a G-homomorphism![]() .
.
To study the coordinate groups of equations in a given fixed group G it is convenient to consider the category of G-groups, that is groups which contain the group G as a distinguished subgroup. If H and K are
G-groups then a homomorphism ![]() is a G-homomorphism if
is a G-homomorphism if ![]() for every
for every![]() . In the
. In the
category of G-groups morphisms are G-homomorphisms; subgroups are G-subgroups, etc. For most of our applications we consider the group G to be a CSA-group.
By ![]() we denote the set of all G-homomorphisms from H into K. It is not hard to see that
we denote the set of all G-homomorphisms from H into K. It is not hard to see that
![]() is a free object in the category of G-groups. This group is called a free G-group with basis X. A G-group H is a finitely generated G-group if there exists a finite subset
is a free object in the category of G-groups. This group is called a free G-group with basis X. A G-group H is a finitely generated G-group if there exists a finite subset ![]() such that the set
such that the set ![]() generates H.
generates H.
A Zariski topology is defined on ![]() by taking algebraic sets in
by taking algebraic sets in ![]() as a sub-basis for the closed sets of this topology. If G is a non-abelian CSA group, in particular, a non-abelian fully residually free group, then the union of two algebraic sets is again algebraic. Therefore the closed sets in the Zariski topology over G are precisely the algebraic sets.
as a sub-basis for the closed sets of this topology. If G is a non-abelian CSA group, in particular, a non-abelian fully residually free group, then the union of two algebraic sets is again algebraic. Therefore the closed sets in the Zariski topology over G are precisely the algebraic sets.
What did not translate immediately was the Noetherian property which is crucial in classicial algebraic geomerty. For the group based algebraic geometry, what had to be introduced was equationally Noetherian groups which is the group theoretic counterpart of the Noetherian condition. The Noetherian condition in rings is defined in terms of the ascending chain condition (see [29] ) and implies that every ideal is finitely generated. What is important about this condition in algebraic geometry is the Hilbert Basis theorem that asserts that every
algebraic set is finitely based. That is if S be a set of polynomials in ![]() then
then ![]() for
for
some finite set of polynomials. This is what is recast in terms of group theory. First a G-group H is a group whcih has a distinguished subgroup isomorophic to G. If S is a set of equations over a group G then ![]() is its set of solutions in G.
is its set of solutions in G.
Definition 1 A G-group H is said to be G-equationally Noetherian if for every ![]() and every
and every
subset S of ![]() there exists a finite subset S0 of S such that
there exists a finite subset S0 of S such that
![]()
The first major examples of equationally Noetherian groups are linear groups over commutative Noetherian rings. This was proved originally by Bryant [30] in the one variable case and then extended by Guba [31] to the case of free groups. The general result is the following.
Theorem 11 Let H be a linear group over a commutative, Noetherian ring with unity and in particular a field. Then H is equationally Noetherian.
In particular, it follows that a finitely generated non-abelian free group is equationally noetherian.
Extremely important in the application of the algebraic geometry of groups to the proof of the Tarski problems is the description of the coordinate groups of systems of equations. Radicals of a system of equations and coordinate group are defined as in classical algebraic geometry. Examining the relationship between the coordinate groups and groups embeddable by a sequence of extensions of centralizers in the free exponential group![]() , shows that the coordinate groups of irreducible algebraic varieties are precisely the finitely generated fully residually free groups (limit groups).
, shows that the coordinate groups of irreducible algebraic varieties are precisely the finitely generated fully residually free groups (limit groups).
In addition to the Tarski problems themselves, the quest for a solution has inspired many other results in group theory. This is especially true concerning the theory of solutions of equations within groups. In 1959, Vaught asked the question whether the sentence
![]()
holds in all free groups. Lyndon [32] then proved that for each solution of ![]() in a free group the elements commute pairwise. This result launched the theory of equations over free groups. The first general results in this were due to Lyndon [32] , Lorenc [33] and Appel [34] where they described the solution set of an arbitrary one variable equation over a free group. In 1966 Malcev described the solution set of the equation
in a free group the elements commute pairwise. This result launched the theory of equations over free groups. The first general results in this were due to Lyndon [32] , Lorenc [33] and Appel [34] where they described the solution set of an arbitrary one variable equation over a free group. In 1966 Malcev described the solution set of the equation ![]() over the free group
over the free group![]() , a problem considered earlier by Nielsen (see [35] ). A version of this was also solved by Csorgo, Fine and Rosenberger [35] . Malcev’s solution has the following non-trivial implication for the elementary theory of a free group of rank 2; the set of all free bases of
, a problem considered earlier by Nielsen (see [35] ). A version of this was also solved by Csorgo, Fine and Rosenberger [35] . Malcev’s solution has the following non-trivial implication for the elementary theory of a free group of rank 2; the set of all free bases of ![]() can be defined by a first order formula in the language of group theory. That is the elements
can be defined by a first order formula in the language of group theory. That is the elements ![]() are a free basis if and only if they satisfy the following formula with constants
are a free basis if and only if they satisfy the following formula with constants![]() ;
;
![]()
The focus of study eventually turned to strictly quadratic equations over free groups, that is equations in which every variable x occurs exactly twice as either x or![]() . Group relators that are quadratic have always been essential in combinatorial group theory due to their close connection with surface group relators. Comerford and Edmonds [36] and Grigorchuk and Kurchanov [37] [38] described the solution sets of quadratic equations over arbitrary free groups. Further work of Hoare, Karrass and Solitar shows that every quadratic equation over a free group is automorphically equiavlent to a standard one.
. Group relators that are quadratic have always been essential in combinatorial group theory due to their close connection with surface group relators. Comerford and Edmonds [36] and Grigorchuk and Kurchanov [37] [38] described the solution sets of quadratic equations over arbitrary free groups. Further work of Hoare, Karrass and Solitar shows that every quadratic equation over a free group is automorphically equiavlent to a standard one.
Makanin in 1982 [24] proved that if a given equation over a free group F has a solution in F then this equation has a solution of bounded length and this bound can be effectively computed from the equation itself. Makanin’s work allowed Razborov [26] to describe the solution set of a system of equations over F. Makanin further extended his results [25] , proving that that the universal theory of a non-abelian free group F is algorithmically decidable.
5. Strategy for the Proof
All these components had to be combined and integrated to provide the final proofs. Here we outline the strategy that was followed. Recall that Vaught proved Tarski Conjecture 2 for all free groups of infinite rank and hence reduced the problem to non-abelian free groups of finite rank. Vaught’s main result was that if the infinite rank free group ![]() is a free factor of the infinite rank free group
is a free factor of the infinite rank free group ![]() then
then ![]() is an elementary subgroup of
is an elementary subgroup of![]() , that is the identity map embedding
, that is the identity map embedding ![]() into
into ![]() is an elementary embedding. Sacerdote went on to prove that
is an elementary embedding. Sacerdote went on to prove that
all free groups of finite rank have the same ![]() -theory, that is they satisfy exactly the same
-theory, that is they satisfy exactly the same ![]() (and
(and
equivalently![]() ) sentences. It is Sacerdote’s result that pinpoints the main strategy in solving the whole problem and provides the first step in an induction.
) sentences. It is Sacerdote’s result that pinpoints the main strategy in solving the whole problem and provides the first step in an induction.
The main technique Vaught used in proving the Tarksi conjecture for infinite rank and Sacerdote used for the ![]() -theory is the following, that is known as the Tarski-Vaught Test.
-theory is the following, that is known as the Tarski-Vaught Test.
Tarski-Vaught Test If H is a subgroup of G then H is an elementary subgroup of G if and only if for any
formula ![]() and for any tuple
and for any tuple ![]() of elements from H there exists a
of elements from H there exists a ![]() such that
such that ![]() is satisfied in G implies that there exists
is satisfied in G implies that there exists ![]() such that
such that ![]() is satisfied in H.
is satisfied in H.
Roughly the Tarski-Vaught Test says that a subgroup H of G is an elementary subgroup if and only if H is algebraically closed in G. In analogy with commutative algebra if we consider first order sentences with variables as our equations then any equation with constants from H which has a solution in G already has a solution within H.
If we wish to apply the Tarksi-Vaught Test to the case of a free factor in a free group of finite rank we must then understand the nature of solving equations in free groups and over free groups. The work of Makanin and Razborov became crucial. Their work provided first a method to determine if an equation over a free group was solvable and hence provided a technique for Kharlampovich and Myasnikov to show that the elementary theory of non-abelian free groups was decidable.
Here is where, however, it was the introduction of algebraic geometry over free groups that led to the necessary understanding of groups that have the same elementary theory as a non-abelian free group of finite rank.
The proofs of Kharlampovich-Myasnikov and Sela show that a general system of equations, with a few special cases that must be handled separately, can be shown to be equivalent to what is called a quasi- trianglular system of quadratic equations.
The coordinate groups of such systems are called QT-groups and are limit groups. A special subclass of them, called special NTQ-groups, are precisely the groups that can be shown to have the same elementary theory as the non-abelian free groups.
The structure of the algebraic variety of a system of equations can be broken down by the Makanin-Razborov method and is tied to the group theoretic breakdown of the coordinate groups.
Since the coordinate groups are limit groups this breakdown is well-understood as the JSJ decomposition of limit groups. The JSJ decompositon of a finitely generated group was developed originally by Rips and Sela [39] . It is graph of groups decomposition with abelian edge groups that encodes all other amalgam decompositions of a group.
It is the JSJ decomposition of the coordinbate groups combined with a type of implicit function theorem that provides for a quantifier elimination process that permits an induction starting with Sacerdote’s ![]() -result.
-result.
After all these massive preliminaries the proof itself is then an induction on the number of quantifiers, based on a quantifer elimination process. In the Kharlampovich-Myasnikov approach the quantifier elimination is handled by an implicit function theorem for quadratic systems.
We now describe in a bit more detail how to use the Tarski-Vaught Test to prove Tarski Conjecture 2.
Let ![]() be a free group with basis
be a free group with basis![]() , a countably infinite set. For each positive integer r, let
, a countably infinite set. For each positive integer r, let
![]() be the free factor
be the free factor ![]() of
of![]() . Let
. Let ![]() be as before the usual first order language with equality
be as before the usual first order language with equality
appropriate for group theory and for each ![]() let
let ![]() be the extension of
be the extension of ![]() formed by adjoining the
formed by adjoining the
non-trivial elements of ![]() as new constant symbols.
as new constant symbols.
Without assuming the Tarski Conjectures for each integer ![]() let
let
![]()
be the set of those sentences of ![]() true in every free group containing
true in every free group containing ![]() as a free factor. Sacerdote’s Theorem is that if
as a free factor. Sacerdote’s Theorem is that if ![]() then
then ![]() and
and ![]() satisfy precisely the same existential-universal and
satisfy precisely the same existential-universal and
universal-existential sentences of![]() . Sacerdote’s result is then the starting point although both Kharlam- povich-Myasnikov reprove it. The basic idea is then to use quantifier elimination to reduce everything back to Sacerdote’s result.
. Sacerdote’s result is then the starting point although both Kharlam- povich-Myasnikov reprove it. The basic idea is then to use quantifier elimination to reduce everything back to Sacerdote’s result.
To this end let ![]() be the set of all universal-existential or existential-universal sentences of
be the set of all universal-existential or existential-universal sentences of ![]() true in
true in ![]() and hence true in every free group containing
and hence true in every free group containing ![]() as a free factor. Let
as a free factor. Let ![]() be the set of all
be the set of all
Boolean combinations of![]() . That is
. That is ![]() consists of all those sentences of
consists of all those sentences of ![]() which are
which are
obtained from ![]() by conjunctions, disjunctions and negations. Suppose that we have a sentence
by conjunctions, disjunctions and negations. Suppose that we have a sentence ![]() of
of ![]() which is more complicated than a universal-existential or existential-universal sentence. What is done is to use quantifier elimination to show that there is a sentence
which is more complicated than a universal-existential or existential-universal sentence. What is done is to use quantifier elimination to show that there is a sentence ![]() such that
such that ![]() holds in
holds in ![]() for all
for all ![]() if and only if
if and only if ![]() does. This reduces the whole theorem to Sacerdote’s case and proves that the
does. This reduces the whole theorem to Sacerdote’s case and proves that the
embeddings ![]() are elementary.
are elementary.
The quantifier elimination is handled by an implicit function theorem. Basically consider a universal-
existential sentence of![]() ,
,
![]() (1)
(1)
We wish to show that for ![]() the sentence (1) holds in
the sentence (1) holds in ![]() if and only if it holds in
if and only if it holds in![]() . One
. One
direction is relatively simple. Suppose that (1) holds in![]() . Then for an arbitrary element
. Then for an arbitrary element ![]()
the sentence
![]()
is an existential sentence of ![]() true in
true in![]() . A group
. A group ![]() is discriminated by a group
is discriminated by a group ![]() if for any finite
if for any finite
subset ![]() of non-trivial elements in
of non-trivial elements in ![]() there exists a homomorphism
there exists a homomorphism ![]() with
with![]() .
.
Since ![]() is discriminated by retractions
is discriminated by retractions ![]() it follows that
it follows that
![]()
must hold in![]() . Since
. Since ![]() was arbitrary the original sentence (1) must hold in
was arbitrary the original sentence (1) must hold in![]() .
.
The other way, that (1) holding in ![]() implies that it holds in
implies that it holds in ![]() is the real work. Let
is the real work. Let![]() .
.
From the implicit function theorem it is the case that whenever (1) holds in ![]() there is an ordered n-tuple
there is an ordered n-tuple
![]() from
from ![]() such that
such that
![]()
also holds in![]() . However
. However
![]()
is a universal sentence of![]() . Again from the fact that
. Again from the fact that ![]() is discriminated by retractions
is discriminated by retractions ![]() it
it
follows that ![]() and
and ![]() satisfy the same universal sentences of
satisfy the same universal sentences of![]() .
.
Therefore if (1) holds in ![]() then
then
![]()
holds in ![]() and so (1) must hold in
and so (1) must hold in![]() . The cases where the hypotheses of the implicit function theorem are violated must be treated separately.
. The cases where the hypotheses of the implicit function theorem are violated must be treated separately.
The key idea is that systems of equations can be reduced to certain quadratic systems and further the coordinate groups of such systems are limit groups. Hence limit groups are fundamental. We next summarize all the important properties of fully residually free groups including their relation to the coordinate groups of algebraic varieties.
Theorem 12 Let G be a fully residually free group. Then G satisfies the following properties:
1) G is torsion-free and each subgroup is also fully resiudally free;
2) G is CSA and hence CT. Further if G is finitley generated each abelian subgroup of G is finitely generated and contained in a unique maximal abelian subgroup;
3) If G is finitely generated then G is finitely presented and has only finitely many conjugacy classes of maximal abelian subgroups;
4) G is linear and has a solvable word problem;
5) Every 2-generator subgroup of G is either free or abelian;
6) If ![]() then either G is free of rank 3, or free abelian of rank 3, or a free rank one extension of centralizers of a free group of rank 2.
then either G is free of rank 3, or free abelian of rank 3, or a free rank one extension of centralizers of a free group of rank 2.
The next result summarizes the important equivalences for finitely generated fully residually free groups. These characterize this class of groups in several different ways and then play a crucial role in the proof of the Tarski problems. Number (9) in the theorem is especially important since it ties the class of limit groups to solutions of equations over free groups. We note that fully residually free groups in general need not be finitely generated. For example an infinitely generated free group is certainly fully residually free. However for our applications and for many of the important properties finite generation is crucial.
Theorem 13 Let G be a finitely generated group. Then the following are equivalent:
1) G is fully residually free;
2) G is universally free if G is non-abelian;
3) G is a limit group;
4) G is a constructible limit group;
5) G is a limit of free groups in the Gromov-Hausdorf Topology;
7) G embeds into a non-standard free group, that is an ultrapower of a free group;
8) G embeds into the free Lyndon completion![]() ;
;
9) G is the coordinate group of an irreducible variety over a free group.
We note that this theorem is a general result and can be considered as without constants or coefficients from any particular free group. Each statement has a correspsonding result if we allow coefficients. If F is a particular non-abelian free group then for example in (1) we can say that a finitely generated F-group G is F-discri- minated by F is equivalent to G being universally equivalent to F in the language ![]() where this language allows constants from F.
where this language allows constants from F.
The applications to equations over free groups and hence the solution to the Tarski problems especially uses (8) and (9) in the theorem and we look at these a bit more deeply. Kharlampovich and Myasnikov prove the following result that they call the embedding theorem. This result combined with the fact that the finitely generated subgroups of ![]() are precisely the finitely generated fully residually free groups shows that the finitely generated fully residually free groups are exactly the coordinate groups of irreducible algebraic varieties.
are precisely the finitely generated fully residually free groups shows that the finitely generated fully residually free groups are exactly the coordinate groups of irreducible algebraic varieties.
Theorem 14 (The Embedding Theorem) Given an irreducible system of equations ![]() over a free group F one can effectively embed the coordinate group
over a free group F one can effectively embed the coordinate group ![]() into
into![]() .
.
Corollary 1 The coordinate groups of irreducible algebraic varieties over a free group F are precisely the finitely generated fully residually free groups.
The finitely generated subgroups of ![]() are precisely subgroups of groups built from finitely generated free groups by iterated extensions of centralizers. From Bass-Serre theory then we get that each finitely generated fully residually free group has graph of groups decomposition with cyclic edges. From this we get that each finitely generated fully residually free group has a JSJ decomposition. This breakup of the coordinate group will lead to a breakup of the algebraic variety.
are precisely subgroups of groups built from finitely generated free groups by iterated extensions of centralizers. From Bass-Serre theory then we get that each finitely generated fully residually free group has graph of groups decomposition with cyclic edges. From this we get that each finitely generated fully residually free group has a JSJ decomposition. This breakup of the coordinate group will lead to a breakup of the algebraic variety.
6. Quasi-triangular systems
The big breakthrough in doing applications of the algebraic geometry and particularly in the solution of the Tarski problem came with the discovery that to study the solution sets and hence the varieties of general equations over free groups it was only necessary to study quadratic equations. That is it was proved that not only are the fully residually free groups the coordinate groups of irreducible algebraic varieties but were embedded into the coordinate groups of special systems called NTQ-systems of quadratic equations. The solutions of quadratic equations over free groups were already extensively studied. Further implicit function theorems were developed for such NTQ-systems. Here we introduce the necessary material about quadratic equations and quadratic systems.
Definition 2 An equation ![]() in variables from
in variables from ![]() is quadratic if every variable x from X occurs in S no more than twice each time as x or
is quadratic if every variable x from X occurs in S no more than twice each time as x or![]() .
.
A quadratic equation ![]() need not contain all the variables from X, it can be empty in some variable, linear in some variables or strictly quadratic on some subset of X.
need not contain all the variables from X, it can be empty in some variable, linear in some variables or strictly quadratic on some subset of X.
We now write X instead of ![]() for a finite system
for a finite system![]() . The reason is that we consider X also as a generating system of a group
. The reason is that we consider X also as a generating system of a group ![]() and sometimes split X into pieces
and sometimes split X into pieces![]() .
.
We extend this to G-groups.
Let![]() . Denote by
. Denote by ![]() the set of variables that occur in S.
the set of variables that occur in S.
Definition 3 A set ![]() is called quadratic if every variable from
is called quadratic if every variable from ![]() occurs in each element S not more than twice as either x or
occurs in each element S not more than twice as either x or![]() . The set S is strictly quadratic if every variable x from
. The set S is strictly quadratic if every variable x from ![]() occurs in each element of S exactly twice each time as either x or
occurs in each element of S exactly twice each time as either x or![]() .
.
A system ![]() over G is quadratic (strictly quadratic), if the corresponding set S is quadratic (strictly quadratic). An element of a quadratic (strictly quadratic) set S is called a quadratic or strictly quadratic word respectively. If S is a singelton we just write S for the set.
over G is quadratic (strictly quadratic), if the corresponding set S is quadratic (strictly quadratic). An element of a quadratic (strictly quadratic) set S is called a quadratic or strictly quadratic word respectively. If S is a singelton we just write S for the set.
Quadratic equations can be placed into several standard forms.
Definition 4 A standard quadratic equation over the group G is an equation of one of the following forms (below ![]() are non-trivial elements from G):
are non-trivial elements from G):
![]() (st1)
(st1)
![]() (st2)
(st2)
![]() (st3)
(st3)
![]() (st4)
(st4)
Lemma 1 Let S be a strictly quadratic word over G. Then there is a G-automorphism ![]() such that
such that ![]() is a standard quadratic word over G.
is a standard quadratic word over G.
The proof of this is in [36] .
Definition 5 A standard quadratic equation ![]() over F is called regular if either it is an equation of
over F is called regular if either it is an equation of
the type![]() , or the equation
, or the equation![]() , or it has a non-commutative solution and it is
, or it has a non-commutative solution and it is
not an equation of the type![]() ,
, ![]() ,
,![]() .
.
In what follows we usually write just ![]() or
or![]() . The implicit function theorem over free groups in its simplest form is the following result.
. The implicit function theorem over free groups in its simplest form is the following result.
Theorem 15 (Implicit function theorem) Let ![]() be a regular standard quadratic equation over a
be a regular standard quadratic equation over a
non-abelian free group F and let ![]() be an equation over F,
be an equation over F, ![]() Suppose that for
Suppose that for
any solution ![]() there exists a tuple of elements
there exists a tuple of elements ![]() such that
such that ![]() Then there exists a
Then there exists a
tuple of words![]() , with constants from F, such that
, with constants from F, such that ![]() for any
for any
![]() .
.
The implicit function theorem hence allows for a type of quantifier elimination.
What is next of importance are special types of systems of quadratic equations. First we define quasi- triangular systems.
Definition 6 Let ![]() be disjoint tuples of variables. A system of equations
be disjoint tuples of variables. A system of equations ![]() with
with
coefficients from a free group F of the following form
![]()
is said to be triangular quasi-quadratic if for every i the equation
![]()
is quadratic in the variables from![]() .
.
Denote by ![]() the coordinate group of the subsystem
the coordinate group of the subsystem ![]() of the system
of the system![]() . The system
. The system
![]() is said to be non-degenerate (NTQ) if for each i the equation
is said to be non-degenerate (NTQ) if for each i the equation ![]() has a solution in
has a solution in
![]() .
.
The coordinate group of an NTQ-system is called an NTQ-group. In Sela’s terminology this is called an ![]() - residually free tower. Further if the only abelian subgroups of an NTQ-group G are cyclic then G is hyperbolic and called a special NTQ-group. Sela calls these hyperbolic-
- residually free tower. Further if the only abelian subgroups of an NTQ-group G are cyclic then G is hyperbolic and called a special NTQ-group. Sela calls these hyperbolic-![]() -residually free towers. The proofs of Kharlampovich and Myasnikov and Sela of the elementary embedding of one free group into another have the byproduct that the special NTQ-groups are precisely the finitely generated groups that have the same elementary theory as the class of non-abelian free groups. Further from the JSJ structure of these groups it follows that an orientable surface group of genus
-residually free towers. The proofs of Kharlampovich and Myasnikov and Sela of the elementary embedding of one free group into another have the byproduct that the special NTQ-groups are precisely the finitely generated groups that have the same elementary theory as the class of non-abelian free groups. Further from the JSJ structure of these groups it follows that an orientable surface group of genus ![]() and a non-orientable surface group of genus
and a non-orientable surface group of genus ![]() are special NTQ-groups and hence have precisely the same first-order theory as the class of non-abelian free groups. We call such groups elementary free groups and will discuss them in section 8.
are special NTQ-groups and hence have precisely the same first-order theory as the class of non-abelian free groups. We call such groups elementary free groups and will discuss them in section 8.
Kharlampovich and Myasnikov [1] use these ideas of algebraic geometry to prove that every finitely generated fully residually free group embeds into Lyndon’s group![]() . As remarked earlier it follows from this that finitely generated fully residually free groups must be finitely presented. The proof of the embedding result follows from a sequence of theorems. We mention two of these from the tail end of the sequence (see [1] ).
. As remarked earlier it follows from this that finitely generated fully residually free groups must be finitely presented. The proof of the embedding result follows from a sequence of theorems. We mention two of these from the tail end of the sequence (see [1] ).
Theorem 16 For every finite system ![]() of equations over a free group F one can find effectively a finite family of non-degenerate triangular quasi-quadratic systems
of equations over a free group F one can find effectively a finite family of non-degenerate triangular quasi-quadratic systems ![]() and word mappings
and word mappings
![]()
such that for every ![]() there exists an i and
there exists an i and ![]() for which
for which![]() , that is
, that is
![]()
and all sets ![]() are irreducible. Moreover every irreducible component of
are irreducible. Moreover every irreducible component of ![]() can be obtained as
can be obtained as
the closure of ![]() in the Zariski topology.
in the Zariski topology.
Theorem 17 For a system ![]() over a free group the set
over a free group the set ![]() is irreducible if and only if
is irreducible if and only if ![]()
for a non-degenerate triangular quasi-quadratic system![]() .
.
From the previous two theorems it follows that to consider the coordinate group of a general equation over a free group it can be reduced to looking at the coordinate group of an NTQ-system.
The final necessary component of the proof of the Tarski problems is the elimination process, abbreviated EP by Kharlampovich and Myasnikov. This is the most technical and difficult portion of the program and is based on initial work of Makanin and then improved upon by Razborov.
In general a quantifier elimination is a concept of simplification used in mathematical logic and model theory. First order formulas with fewer quantifiers are considered simpler with quantifier-free formulas as the simplest. A theory has quantifier elimination if for every formula in the theory there is another formula with fewer quantifiers logically equivalent to it relative to the theory.
Quantifier elimination permits an induction on the number of quantifiers. A first order theory L has quantifier elimination if and only if for any two models B and C of the theory with a common substructure A, B and C are elementarily equivalent in the language of L augmented with constants from A. To prove the elementary equivalence of B and C under quantifier elimination it suffices to prove the equivalence of the existential theory.
The proofs of the Tarksi theorems by Kharlampovich and Myasnikov use an elimination process originally introduced by Makanin. This elimination process, that is abbreviated EP, is a symbolic rewriting process that transforms formal systems of equations in groups. Makanin in 1982 introduced the initial version of the EP. His method provides a decision algorithm to verify consistency of a given system of equations, that is he handles the decidability of the Diophantine problem over free groups. To accomplish this, Makanin estimates the length of the minimal solution (if it exists). As part of this EP, Makanin introduced the fundamental notions of generalized equations and elementary and entire transformations. In 1987, Razborov [26] extended the EP much further. Razborov?s version of the EP produces all solutions of a given system in a free group F. He used special groups of automorphisms, and fundamental sequences to encode solutions.
In 1996 Kharlampovich and Myasnikov, building on the above, found an effective description of solutions of equations over free and fully residually free groups in terms of NTQ systems . In particular they represented a solution set of a system of equations canonically as a union of solutions of a finite family of NTQ groups.
Theorem 18 (see [5] ) One can effectively construct the EP that starts with an arbitrary system ![]() and results in finitely many NTQ systems
and results in finitely many NTQ systems
![]()
such that
![]()
for some word mappings![]() .
.
The word mapping ![]() maps a tuple
maps a tuple ![]() to a tuple
to a tuple![]() .
. ![]() may be pictured as an A-automorphism from
may be pictured as an A-automorphism from ![]() into
into![]() , then any solution
, then any solution ![]() precomposed with
precomposed with ![]() provides a solution
provides a solution![]() .
.
The elimination process in this case can be viewed as a non-commutative analog of the classical elimination process in algebraic geometry. Hence, going from the bottom to the top, every solution of the subsystem ![]() then can be extended to a solution of the next equation
then can be extended to a solution of the next equation![]() . The effectiveness of the EP allows for the determination of the decidability of the first order theory of free groups.
. The effectiveness of the EP allows for the determination of the decidability of the first order theory of free groups.
The crux of the elimination process as applied to systems of equations over a free group F is the following chain of ideas. The precise details can be found in [5] .
Given a system ![]() of equations in a free group
of equations in a free group ![]() one can effectively construct a finite set of generalized equations
one can effectively construct a finite set of generalized equations
![]()
such that:
1) Given a solution of ![]() in
in ![]() one can effectively construct a reduced solution of one of
one can effectively construct a reduced solution of one of ![]()
in the free semigroup with basis![]() ;
;
2) Given a solution of some ![]() in the free semigroup with basis
in the free semigroup with basis ![]() one can effectively construct a solution of
one can effectively construct a solution of ![]() in
in![]() ;
;
3) Given a generalized equation ![]() there are finitely many elementary transformations that can be applied to get a new generalized equation
there are finitely many elementary transformations that can be applied to get a new generalized equation ![]() such that if
such that if ![]() is a solution of
is a solution of ![]() then
then ![]() is a solution of
is a solution of![]() ;
;
4) The elimination process is a sequence of elementary transformations, applied according to some precise rules to an initial pair![]() :
:
![]()
5) The EP is a branching process such that on each step one of the finite number of elementary transfor- mations is applied according to some precise set of rules to form the sequence above;
6) From a group theoretic point of view the elimination process provides information about the coordinate groups of the systems involved. This allows the transformation of the pure combinatorial and algorithmic results obtained in the elimination process into statements about the coordinate groups.
7. The Proof Itself
In [5] in the Kharlampovich-Myasnikov proof, these various ingredients, the reduction to NTQ systems, the description of the breakup of the coordinate groups of equations in terms of the JSJ decomposition of the groups and the corresponding breakup of the algebraic varieties and finally the implicit funciton theorem and quantifier elimination given by the elimination process, was put together to give the final proof that if a free group ![]() is a free factor of the free group
is a free factor of the free group ![]() then it is an elementary subgroup. The techniques of this proof also prove the decidability. Sela’s proof proceeds in much the same way but with different terminology.
then it is an elementary subgroup. The techniques of this proof also prove the decidability. Sela’s proof proceeds in much the same way but with different terminology.
As pointed out, the basic strategy is an induction on the number of quantifiers. The starting off point for the induction is Sacerdote’s theorem which says that if ![]() is a free factor of
is a free factor of ![]() then they satisfy exactly the same
then they satisfy exactly the same ![]() -theories, that is exactly the same
-theories, that is exactly the same ![]() sentences. Sacerdote’s proof is complicated and not entirely clear so both Kharlampovich-Myasnikov and Sela reprove it using their own machinery. However in the case of Kharlampovich-Myasnikov this also provides a technique for the induction step.
sentences. Sacerdote’s proof is complicated and not entirely clear so both Kharlampovich-Myasnikov and Sela reprove it using their own machinery. However in the case of Kharlampovich-Myasnikov this also provides a technique for the induction step.
Recall that Merzlyakov proved that all non-abelian free groups satisfy exactly the positive sentences. Sacerdote, in his proof for the ![]() -theory, used Merzlyakov’s ideas and the small cancellation technique in Van-Kampen diagrams for group presentations (see [15] ). Sacerdote shows that an arbitrary
-theory, used Merzlyakov’s ideas and the small cancellation technique in Van-Kampen diagrams for group presentations (see [15] ). Sacerdote shows that an arbitrary ![]() -sentence is either positive, in which case Merzlyakov’s result can be used, or by using the topology of the Van-Kampen diagrams can be written as a boolean combination of positive sentences and sentences with only one quantifier. It follows from Sacerdote’s theorem that free non-abelian groups of finite rank satisfy the same boolean combinations of
-sentence is either positive, in which case Merzlyakov’s result can be used, or by using the topology of the Van-Kampen diagrams can be written as a boolean combination of positive sentences and sentences with only one quantifier. It follows from Sacerdote’s theorem that free non-abelian groups of finite rank satisfy the same boolean combinations of ![]() -sentences. In Myasnikov-Kharlampovich’s handling of Sacerdote’s result they follow the same idea as Sacerdote to reduce to either positive sentences and apply Merzlyakov’s result or to a boolean combination of positive sentences and sentences with only one quantifier. To get the quantifier elimination they rely on their implicit funcion theorem coupled with their extension of the Makanin-Razborov diagrams. This replaces Sacerdote’s use of van-Kampen diagrams. There are several special cases where the implicit function theorem does not apply directly and these are handled separately. The details are intricate and can be found in [5] .
-sentences. In Myasnikov-Kharlampovich’s handling of Sacerdote’s result they follow the same idea as Sacerdote to reduce to either positive sentences and apply Merzlyakov’s result or to a boolean combination of positive sentences and sentences with only one quantifier. To get the quantifier elimination they rely on their implicit funcion theorem coupled with their extension of the Makanin-Razborov diagrams. This replaces Sacerdote’s use of van-Kampen diagrams. There are several special cases where the implicit function theorem does not apply directly and these are handled separately. The details are intricate and can be found in [5] .
Thus Sacerdote’s theorem on ![]() -sentences is the first step in an induction. For the inductive step they consider a general sentence
-sentences is the first step in an induction. For the inductive step they consider a general sentence
![]()
where U and V are non-trivial elements in the free grup![]() . To prove the Tarski Elementary Embedding Theorem it is shown that this sentence is true if and only if some boolean combination of sentences with less alternations of quantifiers is true and further the reduction does not depend on the free group F nor even on the coordinate group
. To prove the Tarski Elementary Embedding Theorem it is shown that this sentence is true if and only if some boolean combination of sentences with less alternations of quantifiers is true and further the reduction does not depend on the free group F nor even on the coordinate group![]() . Ultimately this reduction leads to Boolean combinations of
. Ultimately this reduction leads to Boolean combinations of ![]() -sentences and hence Sacerdote’s theorem can be used completing the induction. As for Sacerdote’s result the details are complicated and can be found in [5] .
-sentences and hence Sacerdote’s theorem can be used completing the induction. As for Sacerdote’s result the details are complicated and can be found in [5] .
In order to arrive at this reduction, the following ideas, that we have introduced in the previous sections, must be interwoven.
1) The solution set of a systems of equations ![]() over a free group depends on its coordinate group
over a free group depends on its coordinate group ![]() where
where ![]() is the radical of the system. Further general varieties break up into irreducible algebraic varieties and further the finitely generated fully residually free groups, that is the limit groups, are precisely the coordinate groups of irreducible algebraic varieties;
is the radical of the system. Further general varieties break up into irreducible algebraic varieties and further the finitely generated fully residually free groups, that is the limit groups, are precisely the coordinate groups of irreducible algebraic varieties;
2) Finitely generated fully residually free groups can be embedded into the coordinate groups of NTQ- systems. This allows us in trying to solve our general system to concentrate on NTQ-systems. As we have seen these systems are constructed inductively from quadratic equations and we can then apply the techniques developed for quadratic equations to the study of these systems;
3) The implicit function theorem for algebraic varieties corresponding to regular quadratic and NTQ-systems over free groups. As a by-product of placing these ideas together in the proof it will follow that the coordinate groups or special NTQ-systems turn out to form the class of finitely generated elementary free groups, that is the class of finitely generated groups elementarily equivalent to a non-abelian free group. We note that any non- standard free group, that is a proper ultrapower ![]() of a non-abelian free group, is elementary free but not finitely generated;
of a non-abelian free group, is elementary free but not finitely generated;
4) The variation and extension of the Makanin-Razborov process for solving equations over free groups. This extension provides a description of the solution set of a system of equations in a free group as a diagram of homomorphisms tied together with a decomposition of the coordinate group. This leads to what are called generalized equations and an elimination process.
Now consider the general sentence above, and we assume that there are more than two alternations of quantifiers so that it is not a ![]() -sentence:
-sentence:
![]()
If this sentence is positive then it is true or false in every non-abelian free group independent of rank by Merzljakov’s result. If not consider the algebraic variety of this equation and the corresponding system given by the irreducible algebraic components. Call this resulting system ![]() and the corresponding coordinate group
and the corresponding coordinate group
![]() . This is a fully residually free group and from the embdedding of these into coordinate groups of
. This is a fully residually free group and from the embdedding of these into coordinate groups of
NTQ-systems we can look at the equivalent NTQ-system. Now using the extended Makanin-Razborov elimination process combined with the implicit function theorem we can reduce the NTQ-system to a system with a fewer number of quantifiers. The elimination process is a branching process and hence grows in size. A difficult portion of the analysis is to show that this process is finite, that is, it will terminate in a finite number of steps (see [5] ).
Ultimately we get that our original system is equivalent to a system that can be written as a boolean combination of sentences with less alternations of quantifiers. Further this reduction does not depend on the particular coordinate group ![]() only the general properties (1) through (4) above.
only the general properties (1) through (4) above.
This argument proves the Tarski Conjecture in the strong second form and hence also proves the first Tarski Conjecture. The argument also proves the following three results. The first was originally formulated and proved by Sela [9] .
Theorem 19 Every formula in the language of a free group is equivalent to a boolean combination of ![]() - formulas.
- formulas.
Theorem 20 A coordinate group of a special regular NTQ-system has the same elementary theory as a non-abelian free group.
In [4] it was proved that any finitely generated group which is ![]() -equivalent to a non-abelian free group is isomorphic to the coordinate group of a regular NTQ-system. Combining this with Theorem 7.2 gives the complete characterization of finitely generated groups with exactly the same first order theory as the non-abelian free groups. Such groups are called elementary free groups or elementarily free groups.
-equivalent to a non-abelian free group is isomorphic to the coordinate group of a regular NTQ-system. Combining this with Theorem 7.2 gives the complete characterization of finitely generated groups with exactly the same first order theory as the non-abelian free groups. Such groups are called elementary free groups or elementarily free groups.
Theorem 21 A finitely generated group G is an elementary free group if and only G is isomorphic to the coordinate group of a regular NTQ-system. We call such groups NTQ-groups.
We note that Sela of course comes up with the same characterization. In his language the NTQ-groups are called w-residually free towers. Therefore from Sela the finitely generated elementary free groups are the hyperbolic-w-residually free towers.
In the final section we will look in more detail at elementary free groups.
Above we have outlined the proof of the first two Tarski Conjectures in the strongest possible form. That is,
the free group ![]() freely generated by
freely generated by ![]() is an elementary subgroup of
is an elementary subgroup of ![]()
for every ![]() and
and![]() . This leaves us the third Tarski Conjecture, that the elementary theory Th(F) of a non-abelian free group is decidable. This was proved by Kharlampovich and Myasnikov along the same lines using induction as the proof in the last section by showing that each reduction is in fact effective. By effective we mean algorithmic in a finite number of steps.
. This leaves us the third Tarski Conjecture, that the elementary theory Th(F) of a non-abelian free group is decidable. This was proved by Kharlampovich and Myasnikov along the same lines using induction as the proof in the last section by showing that each reduction is in fact effective. By effective we mean algorithmic in a finite number of steps.
Recall that a theory of a group G, Th(G), is decidable if there exists a recursive algorithm which, given a sentence ![]() of
of![]() , decides whether or not
, decides whether or not ![]() is true. For the class of non-abelian free groups the decidability means that there exists a recursive algorithm which, given a sentence
is true. For the class of non-abelian free groups the decidability means that there exists a recursive algorithm which, given a sentence ![]() of
of![]() , decides whether or not
, decides whether or not ![]() is true in every non-abelian free group. The proof of Kharlampovich and Myasnikov is even a bit stronger. There
is true in every non-abelian free group. The proof of Kharlampovich and Myasnikov is even a bit stronger. There
exists a recursive algorithm which, given a sentence ![]() of
of![]() , decides whether or not
, decides whether or not ![]() is true, where
is true, where
![]() allows constants from the free group F.
allows constants from the free group F.
The starting off point for the proof of the decidability of the theory of non-abelian free groups was the work of Makanin. Makanin [24] proved the algorithmic decidability of the Diophantine problem over free groups. He combined this with Merzjlakov’s proof that all non-abelian free groups share the same positive theory to prove the algorithmic decidability of the positive theory of non-abelian free groups. He further proved the algorithmic decidability of the universal theory. This then implies, although it was not relevant at the time, the algorithmic decidability of the universal theory of limit groups. Makanin developed a powerful machinery, which is now called the Makanin elimination process, to deal with equations over free groups. Razborov extended Makanin’s method and described the solution set of an arbitary system of equations over a free group in terms of Makanin-Razborov diagrams. As we have seen the Makanin-Razborov process for describing the solution sets of arbitrary systems of equations can be reduced to examining the solution sets of NTQ systems and hence the solution of quadratic equations.
Kharlampovich and Myasnikov combined the same type of induction process outlined in section 6, together with Makanin’s technique to obtain the decidability of the elementary theory of a non-abelian free group.
What is done, although as in the previous section the details are complicated, is to show the decidability of the ![]() -sentences. Then in the elimination process, based on generalized equations and the extended Makanin- Razborov process, each reduction is algorithmically effective, that is can be done algorithmically. It follows that the decidability question also fits into the induction scheme and carries through. Some of the proofs involving
-sentences. Then in the elimination process, based on generalized equations and the extended Makanin- Razborov process, each reduction is algorithmically effective, that is can be done algorithmically. It follows that the decidability question also fits into the induction scheme and carries through. Some of the proofs involving
effectiveness have been simplified by using the description of limit groups in terms of infinite words in![]() .
.
Further some of the reductions are handled by an extended implicit function theorem.
8. Elementary Free Groups
As a by-product of the proof of the Tarski theorems it is possible to give complete characterizations of those finitely generated groups that have exactly the same first order theory as the non-abelian free groups. Such groups are called elementary free groups (or elementarily free groups) and extend beyond the class of purely non- abelian free groups. In the Kharlampovich-Myasnikov approach these are the special NTQ-groups and in the Sela approach the hyperbolic ![]() -residually free towers. The primary examples of non-free elementary free groups are the orientable surface groups
-residually free towers. The primary examples of non-free elementary free groups are the orientable surface groups ![]() of genus
of genus ![]() and the non-orientable surface groups
and the non-orientable surface groups ![]() of genus
of genus![]() . That these groups are elementary free provides a powerful tool to prove some results concerning surface groups that are otherwise quite difficult. For example Howie [40] and independently Bogopolski and Bogopolski and Svirodov [41] [42] proved that a theorem of Magnus about the normal closures of elements in free groups held also in surface groups of appropriate genus. Their proofs were non-trivial. However it was proved (see [43] [44] and [45] ) that this result was first order and hence automatically true in any elementary free group. In [43] a large collection of such results was given. Such results were called something for nothing results. Of course any such first order result true in a non-abelian free group must hold in any elementary free group. However elementary free groups satisfy many other properties beyond first order results. This second idea was explored in the paper [44] . In this final section we survey briefly these two ideas.
. That these groups are elementary free provides a powerful tool to prove some results concerning surface groups that are otherwise quite difficult. For example Howie [40] and independently Bogopolski and Bogopolski and Svirodov [41] [42] proved that a theorem of Magnus about the normal closures of elements in free groups held also in surface groups of appropriate genus. Their proofs were non-trivial. However it was proved (see [43] [44] and [45] ) that this result was first order and hence automatically true in any elementary free group. In [43] a large collection of such results was given. Such results were called something for nothing results. Of course any such first order result true in a non-abelian free group must hold in any elementary free group. However elementary free groups satisfy many other properties beyond first order results. This second idea was explored in the paper [44] . In this final section we survey briefly these two ideas.
Magnus proved the following theorem about the normal closures of elements in non-abelian free groups:
Theorem 22 (Magnus) Let F be a non-abelian free group and![]() . Then if
. Then if![]() , it follows
, it follows
that R is conjugate to either S or![]() . Here
. Here ![]() denotes the normal closure in F of the element g.
denotes the normal closure in F of the element g.
Howie [40] and independently Bogopolski [41] and Bogopolski and Sviridov [42] gave a proof of this for surface groups. Howie’s proof was for orientable surface groups while Bogopolski and Sviridov also handled the non-orientable case. Their proofs were non-trivial and Howie’s proof used the topological properties of surface groups. Howie further developed, as part of his proof of Magnus’ theorem for surface groups, a theory of one- relator surface groups. These are surface groups modulo a single additional relator. Bogopolski and Sviridov proved in addition that Magnus’s Theorem held in even a wider class of groups. In [43] (see also [44] and [45] ) Magnus’ result is actually a first-order theorem on non-abelian free groups and hence from the theorems con- cerning the solution of the Tarski problems it holds automatically in all elementary free groups. In particular, Magnus’ theorem will hold in surface groups, both orientable and non-orientable of appropriate genus. If G is a group and![]() , then
, then![]() , as in the statement of Magnus’s Theorem above, will denote the normal closure in G of the element g.
, as in the statement of Magnus’s Theorem above, will denote the normal closure in G of the element g.
Theorem 23 Let G be an elementary free group and![]() . Then if
. Then if ![]() it follows that R is conjugate to either S or
it follows that R is conjugate to either S or![]() .
.
As corollaries we recover the results of Howie [40] , Bogopolski [41] and Bogopolski-Sviridov [42] which extend Magnus’s Theorem to surface groups
Corollary 2 ([40] [41] ) Let ![]() be an orientable surface group of genus
be an orientable surface group of genus![]() . Then
. Then ![]() satisfies Magnus’s theorem, that is if
satisfies Magnus’s theorem, that is if ![]() and
and ![]() it follows that u is conjugate to either
it follows that u is conjugate to either ![]() or
or![]() .
.
Corollary 3 ([42] ) Let ![]() be a non-orientable surface group of genus
be a non-orientable surface group of genus![]() . Then
. Then ![]() satisfies Magnus’s theorem, that is if
satisfies Magnus’s theorem, that is if ![]() and
and ![]() it follows that u is conjugate to either
it follows that u is conjugate to either ![]() or
or![]() . The genus
. The genus ![]() is essential here.
is essential here.
In [43] a collection of results about elementary free groups and surface groups was presented, their proofs being consequences of the Tarski theorem. We mention one such result that is not obvious in a surface group. The following theorem can be easily proved in free groups.
Theorem 24 Let F be a free group and n, k non-zero integers. For all ![]() if
if ![]() then
then
either ![]() or
or ![]() commute and both are powers of a single element.
commute and both are powers of a single element.
The first part of the result that either ![]() or
or ![]() is first-order given by a sequence of elementary
is first-order given by a sequence of elementary
sentences, one for each ![]() with neither n nor k zero;
with neither n nor k zero;
![]()
Therefore this part of the result must hold in any elementary free group. Further if the elementary free group is finitely generated the second part must also hold.
Corollary 4 Let G be an elementary free group. If ![]() and if
and if ![]() then either
then either
![]() or x, y commute. If G is finitely generated then both x and y are powers of a single element
or x, y commute. If G is finitely generated then both x and y are powers of a single element![]() .
.
Since surface groups are finitely generated we have the following.
Corollary 5 Let G be either an orientable surface group of genus ![]() or a non-orientable surface
or a non-orientable surface
group of genus![]() . If
. If ![]() and if
and if ![]() then either
then either ![]() or x, y commute and then
or x, y commute and then
both x and y are powers of a single element![]() .
.
In another direction in [44] properties of all elementary free groups, which may not be first order were explored. A finitely generated elementary free group G must be a limit group and many of its properties follow from from the structure theory of limit groups. Hence such a group must be CSA and any 2-generator subgroup is either free or abelian.
In [44] it was proved that a finitely generated elementary free group has cyclic centralizers. This is not a first order statement, however from this we get that if two elements commute in a finitely generated elementary free group then they are both powers of a single element. This is not true in a general elementary free group. An example where it does not hold in the infinitely generated case is given in [44] . From the cyclic centralizer property we can obtain that a finitely generated elementary free group must be hyperbolic, stably hyperbolic and a Turner group, that is the test elements, if there are any, in any finitely generated elementary free group are precisely those elements that do not lie in any proper retract. It was also proved in [44] that any finitely generated elementary free group is conjugacy separable and hence has a solvable conjugacy problem. In [46] (see also [47] ) is was shown the automorphism group of a finitely generated elementary free group is tame.
The next theorem summarizes many of these results. The proofs can be found [44] .
Theorem 25 Let ![]() be a finitely generated elementary free group. Then:
be a finitely generated elementary free group. Then:
1) (Magnus’s Theorem) if ![]() if
if ![]() it follows that
it follows that ![]() is conjugate to either
is conjugate to either ![]() or
or![]() ;
;
2) G has cyclic centralizers of non-trivial elements. It follows that if ![]() and x, y commute then both x and y are powers of a single element
and x, y commute then both x and y are powers of a single element![]() ;
;
3) if ![]() with
with ![]() and
and ![]() in the subgroup generated by
in the subgroup generated by ![]() it follows that if
it follows that if ![]() is
is
conjugate to a power of ![]() within
within ![]() that is there exists a
that is there exists a ![]() with
with ![]() for some
for some
![]() and
and ![]() it follows that
it follows that![]() . Further if
. Further if ![]() then
then ![]() is conjugate within
is conjugate within
![]() to or;
to or;
4) G is conjugacy separable;
5) G is hyperbolic and stably hyperbolic;
6) G is a Turner group, that is the test elements in G are precisely those elements that do not fall in a proper retract;
7) if G is freely indecomposable then the automorphism group of G is tame;
8) G has a faithful representation in![]() .
.
For more information on elementary theory in general, see [11] -[13] . For further information on the structure of limit groups and hyperbolic groups see [21] [48] -[51] [52] [53] .