1. Introduction
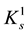 is a very interesting component of S-convexity, not to say exotic: It differs substantially from
is a very interesting component of S-convexity, not to say exotic: It differs substantially from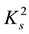 , yet, in a certain sense, seems to supplement it.
, yet, in a certain sense, seems to supplement it.
According to the scientific literature, Hudzik and Maligranda [3] would have been the first researchers to mention the phenomenon S-convexity. They themselves, however, in the paper we have just cited, blame Orlicz for the appearance of the phenomenon.
We had contact with the phenomenon because of the work of Dragomir and Pearce [4] and they seem to be the only people to try to further develop the theory of Hudzik and Maligranda until we start working with the topic, having been asked to do so by the own Dragomir.
Sofo, who worked in the same university as Dragomir in 2001, when we met both, also asked us to work with the topic.
The university where we all worked (Pinheiro, Dragomir, and Sofo) in that 2001 was called Victoria University of Technology.
We actually tried to communicate with both Hudzik and Maligranda in that 2001 by means of the electronic addresses that we found on the Internet for them. Even though the addresses seemed to work (the electronic letters never bounced), they never replied.
Hudzik and Maligranda published their paper in 1994 and we started working with the topic in 2001.
Dragomir’s book dates from 2002, but we helped revise it in 2001.
Some interesting results regarding this phenomenon have been attained by Dragomir in 1999 [5] , as we can see in [4] .
Our first results had to do with the shape of S-convexity 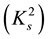 and were presented in a face-to-face mode to Dragomir and, later on, in a talk at the own VUT in the own 2001.
and were presented in a face-to-face mode to Dragomir and, later on, in a talk at the own VUT in the own 2001.
We submitted the same paper we published in 2007 with Aequationes Mathematicae [6] in 2001 to the same Aequationes Mathematicae but, for some reason, they only accepted publishing it in 2007, that is, six years later.
Because of that, our first publication on the topic was [7] .
Notation
We use the symbols from [8] here:
・ 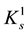 for the class s-convex functions in the first sense, where
for the class s-convex functions in the first sense, where ;
;
・ 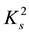 for the class s-convex functions in the second sense, where
for the class s-convex functions in the second sense, where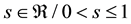 ;
;
・ 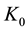 for the class convex functions;
for the class convex functions;
・ 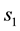 for the variable s,
for the variable s,  , used for the first type of s-convexity;
, used for the first type of s-convexity;
・ 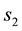 for the variable s,
for the variable s, 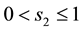 , used for the second type of s-convexity.
, used for the second type of s-convexity.
Remark 1. The class 1-convex functions is simply a subclass of the class Convex Functions. If we make the domain of the convex functions be inside of the set of the non-negative real numbers, we then have the class 1-convex functions: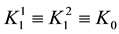 .
.
The definition, for![]() , so far, is [8] :
, so far, is [8] :
Definition 1. A function ![]() is said to be s1-convex if the inequality
is said to be s1-convex if the inequality
![]()
holds![]() .
.
Remark 2. If the inequality is obeyed in the reverse1 situation by f, then f is told to be s1-concave.
Trivially, we need to get rid of one of the variables in this definition, just like we did in [1] .
After doing that, our definition will look like this:
Definition 2. A function ![]() is said to be s1-convex if the inequality
is said to be s1-convex if the inequality
![]()
holds![]() .
.
As seen in [9] , the domain should be in![]() , not in
, not in![]() , and this is also because we want to extend the concept of convexity and the domain, in the definition of the Convexity Phenomenon, is a slice of
, and this is also because we want to extend the concept of convexity and the domain, in the definition of the Convexity Phenomenon, is a slice of![]() . After changing this little detail, our definition is:
. After changing this little detail, our definition is:
Definition 3. A function ![]() is said to be s1-convex if the inequality
is said to be s1-convex if the inequality
![]()
holds![]() .
.
Because we know that s1 should be between 0 and 1 and there is no reason to exclude ![]() as a possible replacement for X, we should word our definition in the following way:
as a possible replacement for X, we should word our definition in the following way:
Definition 4. A function ![]() is said to be s1-convex if the inequality
is said to be s1-convex if the inequality
![]()
holds![]() .
.
The original definition, for![]() , was actually the one we mentioned in [7] :
, was actually the one we mentioned in [7] :
Definition 5. A function ![]() is said to be s-convex in the first sense if
is said to be s-convex in the first sense if![]() ,
, ![]() and
and ![]() with
with![]() .
.
To go from the original definition to our modified version, we not only did all that we have already written about, but we also considered the results attained in [7] plus the fact that if![]() , then
, then ![]() (we
(we
call ![]()
![]() and a is then
and a is then![]() . b, on the other hand, is
. b, on the other hand, is![]() ).
).
2. S1-Convexity DOES NOT Extend Convexity
![]() is a simple counter-example to the claim that S1-convexity extends convexity. See:
is a simple counter-example to the claim that S1-convexity extends convexity. See:
・ The left side of the definition inequality becomes![]() .
.
・ The right side of the definition inequality becomes![]() .
.
・ Because![]() ,
,![]() .
.
・ The same will happen to the other addend:![]() , and then
, and then![]() .
.
・ We conclude that ![]() whenever
whenever ![]() and therefore that
and therefore that
![]() ,
,
which is precisely the opposite to what we needed to get to be able to assert that![]() .
.
(**) We will, on the next paragraph, prove the supplementary theorem to the theorem whose proof we have rewritten in [2] , but it is true that the current definition of S1-convexity covers at most nondecreasing real functions, as for the interval![]() , and at most non-increasing real functions, as for the interval
, and at most non-increasing real functions, as for the interval![]() .
.
Theorem 1. Let![]() . If
. If![]() , then f is non-increasing on
, then f is non-increasing on![]() .
.
Proof. When we apply the definition of s1-convexity to a function that satisfies the conditions of this theorem,
![]() will always be inside of the inclusions, so that we can use it in our proof with no loss.
will always be inside of the inclusions, so that we can use it in our proof with no loss.
In replacing ![]() with
with ![]() in our definition, we get
in our definition, we get![]() .
.
Following the reasoning we have presented in [2] , we can now equate x to ![]() or make
or make ![]() be as meaningless as wanted.
be as meaningless as wanted.
Our inequality then becomes ![]() or
or![]() .
.
Because ![]() in our theorem, we have
in our theorem, we have ![]() and therefore
and therefore![]() , what implies
, what implies![]() . Assuming x is a non-positive number, we get
. Assuming x is a non-positive number, we get![]() .
.
In this case, we can only have a non-increasing function: (![]() and
and![]() ).
).
Because the Convexity Phenomenon covers all types of functions in what comes to growth, S1-convexity cannot be told to be an extension of convexity: According to (**), it is not covering decreasing real functions inside of the interval ![]() and it is not covering increasing real functions inside of the interval
and it is not covering increasing real functions inside of the interval![]() .
.
3. Conclusions
We believe that we have now proven, once and for all, that the S1-convexity Phenomenon cannot possibly be a proper extension of the Convexity Phenomenon: Easy counter-examples are found, and at least two theorems that make us be able to generate an infinity of convex functions that are not contained in the set of s1-convex functions exist and seem to be very sound.
We shall, therefore, and from now onwards, refer to exclusively ![]() when talking about extensions of the convexity phenomenon.
when talking about extensions of the convexity phenomenon.
We may still try to determine the exact shape of the S1-convexity Phenomenon because it is an interesting creation, and several researchers, some of them with hundreds of publications, have already produced results involving it.
NOTES
1Reverse here means >, not ≥.