The Literature Review of Algebra Learning: Focusing on the Contributions to Students’ Difficulties ()
1. Introduction
Algebra has been recognized as a critical milestone in students’ mathematics learning. However, it has been noted that many students created a serious barrier in the algebraic problem solving and formal algebraic system (Kieran, 1992) . Therefore, there has been a great attention paid to addressing students’ difficulties in algebra learning. This paper is going to review the research literature that bears on the contributions to the students’ difficulties in their algebra learning.
In order to evaluate the related literature, 29 articles are selected from my database searching and then categorized into a taxonomy (see Figure 1) including the five categories: algebra content, cognitive gap, teaching is-
sues, learning matters, and transition knowledge. After that, the taxonomy is used to conduct the whole literature review. Within the taxonomy, each category is not independent. For instance, the category of algebra content is the knowledge base for the other four categories. Meanwhile, one of the articles could be coded into more than one category. For instance, the article “ Kieran (1992) ” is coded into four categories such as algebra content, cognitive gap, teaching issues, and learning matters.
Even though the development of taxonomy is not exhaustive, but it provides a perspective of viewing the contributions to the students’ difficulties in algebra learning within the broad ranges, such as mathematics development, school curriculum, teaching practice and students’ learning, and so on.
The rest part of this paper focuses on synthesizing and evaluating the existing researches according to the categories demonstrated in the taxonomy. As for the structure of the synthesization and evaluation, discussions will be made 1) on the didactical cut, structural feature of algebra and the characteristics of school algebra in section 2-algbera content; 2) on the cognitive demands from algebra learning, product-process dilemma, and the students’ difficulties in operating with the unknown in section 3-cognitive gap; 3) on the discontinuity between primary arithmetic and secondary algebra, scarcity in algebra teaching, and three ideas from China and Singapore in section 4-teaching issues; 4) on the students’ difficulties in operational symbols, simplifying expressions, equity, and word problems in section 5-learning matters; and 5) on the needs required by the transition from arithmetic to algebra such as adaptation to a milieu and social interactions and adjustments in Section 6-transi- tion knowledge. Finally, the summary and the research gap are provided in Section 7.
2. Algebra Content
This category centers on the discussion about the nature of algebra including the didactical cut and structural essence presented in the historical development of algebra. Certainly, school algebra is, to a large extent, influenced by these facts.
2.1. Didactical Cut
Filloy and Rojano (1989) defined one of the fundamental ruptures between arithmetic and algebra is a didacticalcut. The notion referred to the transition that occurred as students face such equations as . Students could successfully solve the equation as
. Students could successfully solve the equation as  using reversal operation as subtracting B from D and dividing by A. This type of equation was called by them as “arithmetical” (p. 19). The reversal operation is not applicable for the non-arithmetical equations as
using reversal operation as subtracting B from D and dividing by A. This type of equation was called by them as “arithmetical” (p. 19). The reversal operation is not applicable for the non-arithmetical equations as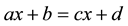 . In order to solve such equations, students have to resort to a truly algebraic idea of operating the unknown (Radford, 2012) . Operating the unknown requires students to think analytically, treating the unknown as if it is known (Radford & Puig, 2007) . This view provides a specific situation which requires the transition from arithmetic to algebra. Certainly, such requirement stems from the structural nature of algebra.
. In order to solve such equations, students have to resort to a truly algebraic idea of operating the unknown (Radford, 2012) . Operating the unknown requires students to think analytically, treating the unknown as if it is known (Radford & Puig, 2007) . This view provides a specific situation which requires the transition from arithmetic to algebra. Certainly, such requirement stems from the structural nature of algebra.
2.2. Structural Algebra
Kieran (1992) had offered a historical account of the development of algebraic symbolism and its transformational rules, which emphasized the distinguished features of letters between representing unknowns in equation solving and representing givens in expressing general solutions. Furthermore, Kieran (1992) analyzed that the development of algebraic symbolism demonstrated a change from a procedural to a structural perspective on algebra. Meanwhile, the structural development of algebra has a considerable impact on school algebra learning.
2.3. School Algebra
In school mathematics, arithmetic is normally treated as numerical computations (Sfard & Linchevski, 1994) . Arithmetic method is used to carry out one or more operations with given numbers to achieve a solution. For elementary algebra, its need is to define the relationships between the unknown and the known data in a problem. As Sadovsky and Sessa (2005: p. 90) pointed out, “the ‘object’ of arithmetic in primary school is numbers, whereas elementary algebra focuses on relationships between quantities”. It is also shown that students’ prior exposure in computing binary operations does not prepare them very well to handle algebra (Banerjee & Subramaniam, 2012) . For instance, students often apply procedures that have been employed in arithmetic context to simplify algebraic expressions and make the similar mistakes (Fischbein & Barash, 1993) .
It is the existing facts in algebra learning that the three categories are the basic barriers and requirements for students’ algebra learning. Therefore, those facts will be involved in other sections, which also demonstrate that the category of algebra content is the foundation of the other categories.
3. Cognitive Gap
Cognitive gap is an obvious obstacle for students’ successful transition from arithmetic to algebra as Sfard (1991) suggested. Such cognitive gaps demonstrated from the previous researches are mainly cognitive demands, “product-process” dilemma, and operating with the unknown.
3.1. Cognitive Demands
Learning algebra requires students to take symbolic representations with little or no semantic content as mathematical objects and operate on these objects through processes that usually do not produce numerical solutions (Kieran, 1992) . It also requires students to modify their prior experiences in arithmetic context and represent the relationships between quantities in word problems with inverse operations used in arithmetic context (Kieran, 1992) . It is clear that the cognitive demands for different operations and representations involved in algebra are intellectual struggles.
3.2. “Product-Process” Dilemma
One cognitive problem was identified by Davis (1975: p. 18) as “name-process” dilemma. The dilemma could be interpreted by the duality “product-process” proposed by Sfard and Linchevski (1993) . For instance, an expression such as 8a is both a product for an answer (name) and a process-multiplying 8 by a. Herscovics and Linchevski (1994) showed that, in a teaching experiment, even after instruction, some students could not recognize 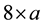 as the area (name or product) of a targeted rectangle unless it was embedded in the area formula “
as the area (name or product) of a targeted rectangle unless it was embedded in the area formula “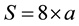 ”. Thus, even after an instruction of elementary algebra, students often experience difficulties in operating on a letter representing an unknown in an equation.
”. Thus, even after an instruction of elementary algebra, students often experience difficulties in operating on a letter representing an unknown in an equation.
3.3. Operating with the Unknown
In order to examine students’ experiences in operating the unknown, Linchevski and Herscovics (1996) used equations with only one occurrence of the unknown (e.g. ) and equations with two occurrences of the unknown on the same sides (e.g.
) and equations with two occurrences of the unknown on the same sides (e.g.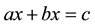 ) and on different sides of the equal sign (e.g.
) and on different sides of the equal sign (e.g. ) to examine the shift in students’ procedures. It was found that students could spontaneously group terms that were purely numeric rather than terms in the unknown, which mean “students could not operate spontaneously with or on the unknown” (Linchevski & Herscovics, 1996: p. 41) .
) to examine the shift in students’ procedures. It was found that students could spontaneously group terms that were purely numeric rather than terms in the unknown, which mean “students could not operate spontaneously with or on the unknown” (Linchevski & Herscovics, 1996: p. 41) .
In addition, during the process of indicating a clear demarcation between arithmetic and algebra, Herscovics and Linchevski (1994) revealed a difficulty of such pre-algebraic nature as a tendency to detach a numeral from the preceding minus sign in the grouping of numerical terms. For example, in , students often add 2 and 5. The high incidence of this mistake demonstrates that the problem is not only common but reflective of unsuspected cognitive obstacles as Herscovics (1989) commented.
, students often add 2 and 5. The high incidence of this mistake demonstrates that the problem is not only common but reflective of unsuspected cognitive obstacles as Herscovics (1989) commented.
It could be drawn to conclusion that the cognitive demands are general requirement from the nature of the algebra. “product-process” dilemma and operating with the unknown stem from the common fact―a letter representing an unknown, which is also part of facts of algebra. Therefore, it could be considered that the cognitive gap is brought about from the nature of algebra.
4. Teaching Issue
Limited is the literature on the teaching issues related to the students’ difficulties in algebra learning as Kieran (1992) commented. Nevertheless, the limited literatures are sorted into three categories: discontinuity, scarcity in algebra teaching, and three ideas.
4.1. Discontinuity
The traditional arithmetic pays attention to training students’ fluency and accuracy in algorithmic computations. While in algebra, students need to have the knowledge and capability of transforming equivalent algebraic expressions. Napaphun (2012) showed that the discontinuity between elementary school arithmetic and the algebra learnt in upper grades was serious. For instance, he mentioned that regarding to the concept of the equal sign, students in most elementary schools were taught to understand the equal sign as a symbol of the calculation. Thus, students habitually thought that an equal sign was always followed by an answer. In fact, recognizing the relation expressed by the equal sign is crucial for algebra learning as Freiman and Lee (2004) suggested.
4.2. Scarcity in Algebra Teaching
Kieran (1992) commented that there was a considerable scarcity not only of teaching models but also of researches on teachers’ beliefs and attitudes in algebra. For instance, she mentioned that the teaching models of algebra were not regarded as the way in a different light from ones of arithmetic or geometry. And the teaching of algebra was inclined to focus on such pedagogical issues as the time spent on whole-group instruction or group work, teaching for procedures or understanding, and constructivist or behaviourist approaches to teaching. She further commented that except for the common pedagogical issues, algebra teachers, as other subject teachers, tended to follow a textbook. There are few reports to deal specifically with algebra teaching.
In addition, Rachlin (1989) furthermore pointed out that there was a need for research on algebra curriculum from both content and teachers’ perspectives. It is not sufficient to modify the algebra content in the textbook in terms of teachers’ heavy reliance on the textbook to change algebra teaching. He suggested that we must understand the nature of teachers’ beliefs and attitudes and the roles these beliefs and attitudes play in their teaching. Therefore, exploring the teaching of algebra in some Asian countries such as China and Singapore is a very expedient approach to address teaching strategies in terms of the distinguished performance by the students in those countries in international tests.
4.3. Three Ideas
Recently, Cai and Moyer (2008) commented on the algebra teaching in China and Singapore for purpose of increasing American teachers’ knowledge and ability to develop students’ algebraic thinking since mathematics achievement in United States was consistently lower than that in those countries. The review suggested that three ideas from Chinese and Singaporean teaching emerging in their reviews were: 1) relating reverse operations to equation solving in Chinese teaching; 2) pictorial equation solving illustrated in Singaporean teaching; and 3) using both arithmetic and algebraic approaches to solve problems in Chinese teaching. Those three ideas were further analyzed by Cai and Moyer (2008) to understand their benefits for students’ transition from arithmetic to algebra according to Kieran’s (2004) five adjustments for successful transition. It was evidenced that the three ideas had matched with four of the five adjustments. Here, the three ideas are highlighted as a reference for the barren teaching consideration.
The discontinued teaching between arithmetic and algebra is very common in many countries. However, some ideas are verified to be effective in algebraic teaching in China and Singapore, which is the contribution to the scarcity in algebraic teaching.
5. Learning Matters
There is large bulk of researches bearing on students’ algebra learning, particularly on students’ misconceiving of various concepts in school algebra. It has been typically indicated from the literature we have targeted that students lacked the relevant understanding of operational symbols, simplifying expressions, equality and equation solving. All the evidence are provided from the following discussions.
5.1. Operational Symbols
Booth (1984) reviewed that school algebra was sometimes taken as generalized arithmetic. This meant that the general statements in algebra represented given arithmetical rules and operations. Therefore, students’ prior experiences of using symbols in arithmetic would impact on their understanding of the meaning associated with formal symbols in algebra. For example, plus sign is typically interpreted as actions to be operated in arithmetic, which is not used in algebra (Behr et al., 1980) . Specifically, Booth (1988) pointed out that, in arithmetic, students were taught to present answers in a single term, such as 3 + 5 was not an acceptable answer. Thus, students were unlikely to recognize a + b to represent a total number of items in two sets owning a and b items, respectively, which further meant that students were unable to regard a + b as a mathematics object in algebra.
In addition, Kiichemann (1981) carried out a large-scale study to examine students’ interpretations of literal terms. He found that a great deal of students (13 - 15 years old) could interpret letters as specific unknowns rather than as generalized numbers. His further finding was that majority of students treated letters as concrete objects or overlooked them, which meant that many students were unable to interpret literal expressions as numerical input-output procedures―the first stage in Sfard’s (1991) developing process of a structural conception of algebraic expressions.
5.2. Simplifying Expressions
Greeno (1982) conducted a study with beginning algebra students to test their conception of structure of relations in problems. He found that students were short of structural understanding of algebra. For instance, they partitioned algebraic expressions into separately component parts. And more often, students’ operation of simplification seemed to be quite at random. For example, 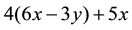 was simplified as
was simplified as 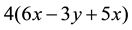 at one time, and as
at one time, and as 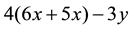 at another time.
at another time.
Wenger (1987) also described the students’ arbitrary strategies when they dealt with simplifications due to the fact that they could not recognize the right things in algebraic expressions. And students were incapable to transform the simplification knowledge they had learned in one context, as polynomials, to another one, as radicals.
Another typical error in simplifying algebraic expressions was concatenation as Welder (2012) illustrated. For example, 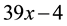 was concatenated quite often by students into
was concatenated quite often by students into 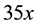 and
and ![]() concatenated into
concatenated into![]() . Carry, Lewis, and Bernard (1980) confirmed that such kind of error occurred not only by beginning algebra students but college students as well. In their study, such error was the most predominant one that students made during their simplifying expressions at different stages of equation solving. Furthermore, they indicated that such error could be caused by students’ over generalizing certain validated operations to achieve a generic operation. Thus, the arbitrary strategies and concatenation approaches are the typical behaviours that students demonstrate in the simplification expressions.
. Carry, Lewis, and Bernard (1980) confirmed that such kind of error occurred not only by beginning algebra students but college students as well. In their study, such error was the most predominant one that students made during their simplifying expressions at different stages of equation solving. Furthermore, they indicated that such error could be caused by students’ over generalizing certain validated operations to achieve a generic operation. Thus, the arbitrary strategies and concatenation approaches are the typical behaviours that students demonstrate in the simplification expressions.
5.3. Equality
Equality is one of the requirements for generating and sufficiently interpreting structural representations such as equation (Kieran, 1992) . It is normally referred to as the left-right equivalent of the equal sign. However, it is shown from researches that the equal sign is too often misinterpreted by students at all levels of education although high school and college students could be more willing to accept the equal sign as formal symbol for equivalence than younger students as Welder (2012) commented.
Behr, Erlwanger and Nichols (1980) revealed that beginning algebra students took the equal sign as a procedural indicator. For example, students were reluctant to accept expressions such as 3 + 4 = 2 + 5 or 3 = 3. They would like to change equality ![]() to be separated into two equalities
to be separated into two equalities ![]() and
and![]() ; equality
; equality ![]() (Welder, 2012) in terms that they would think that the right side should be the answer.
(Welder, 2012) in terms that they would think that the right side should be the answer.
In addition, Falkner, Levi, and Carpenter (1999) further offered specific data for such limited interpretation of the equal sign. In their investigation, all the participations (145 American students from grade 6) could not correctly fill the number sentence![]() . The typical answer for this question was 12 or 17. In addition, the similar situation was presented in the analysis from Li, Ding, Capraro and Capraro (2008) . It was evidenced that there were only 25 out of 105 American Grade 6 students could correctly fill the first blank in such number sentence
. The typical answer for this question was 12 or 17. In addition, the similar situation was presented in the analysis from Li, Ding, Capraro and Capraro (2008) . It was evidenced that there were only 25 out of 105 American Grade 6 students could correctly fill the first blank in such number sentence![]() . However, 91 out of 105 students could give a correct answer 8 for the second blank.
. However, 91 out of 105 students could give a correct answer 8 for the second blank.
In a word, the misunderstanding and ill operation of equal sign impede students from access to the concept of equity which is the core component of the concept of equation in algebra learning.
5.4. Word Problems
Word problems are regarded as stumbling blocks in algebra to access to higher mathematics, even leading students to drop out of mathematics (Cai et al., 2004) . The formal approach used in word problem solving is to formulate an equation or system of equations and operations (Kieran, 1992) . However, the students’ prior arithmetical experiences posed a great influence on their world problem in secondary.
Khng and Lee (2009) reviewed on the influence of secondary students’ prior arithmetical experiences on their word problem solving in Singapore. They commented that algebra word problems were taught in primary school with arithmetic methods, such as counting techniques, guess and test, working backwards, and grouping and model method. And students were very proficient with these methods and regard them as prepotent strategies. Consequently, given the accruing prepotent strategies from primary mathematics, students thought firstly about these strategies rather than algebraic equation formulation when they were presented with word problems in secondary school.
In addition, secondary school teachers often find that beginning algebra students are not motivated to learn the skills needed to solve algebra word problems (Ng & Lee, 2009) . This is partly due to the fact that, with the affordance of a concrete and visual representation for the unknowns and arithmetic procedures to solve for the unknowns, students can avoid engaging with the representational and transformational activities, generalising and justifying activities, activities which students find challenging (Kilpatrick, Swafford, & Findell, 2001) .
Except for the influence from the arithmetic thinking, students have difficulties in formulating an equation or equations system for a word problem. Reed (1987) found that students had difficulties in recognizing and generating the similar structure among problems with different context. Students often resort to different approaches to access the relations or structures involved in a word problems. For example, syntactic translation and substitution of various numbers are used to verify the adequacy of the equations (Reed, Dempster, & Ettinger, 1985) . Tables of relations are also found to be used by students to generate equations for problems; however, repre- senting correct is quite challenging for students (Hoz & Harel, 1989) . Moreover, from the cognitive perspective, it is evidenced that students have considerable difficulty in specifying relations among variables (Chaiklin, 1989) .
Equation solving is another barrier for students’ word problem solving even though they could formulate a correct equation. Students have generally been found to lack the capability to generate and maintain a holistic overview of the structures of an equation, which impacted on the next algebraic transformation to be carried out (Kieran, 1992) . For the multi-operation equations, it is noted that students often make very poor strategic decisions in simplifying algebraic expressions and operations (Carry, Lewis, & Bernard, 1980) .
Word problem solving is the application field of students’ algebraic knowledge including building the relationships between quantities, expressing the relationships by equations, and solving equation. If students get stuck at any one out of the three stages, the word problems would not be solved proficiently.
From the above mentioned discussion on the learning matters, it could be seen that there is much attention paid to the students’ specific challenges in certain topics of algebra learning. The challenges’ explosion could be incurred by all the categories already discussed such as algebra content, cognitive gap, and teaching issues. Thus, the discussed learning matters are consequential phenomena caused by the structural nature of algebra, cognitive gap, and the absence of teaching concerns.
6. Transition Knowledge
There are two kinds of knowledge emerging from the literature to address the knowledge required in the transition from arithmetic to algebra: adaptation to a milieu and social interactions; and the adjustments.
6.1. Adaptation to a Milieu and Social Interaction
Sadovsky and Sessa (2005) aimed to give an account of the emergence of knowledge pertaining to the transition from arithmetic to algebra in the course of an algebra learning classroom with two kinds of interaction such as the adidactic interaction between each student and a given problem, and the adidactic interaction of each student with the procedures of others. It was assumed by them that the processes of adaptation to a milieu and the social interaction were crucial for the transition from arithmetic to algebra.
6.2. Adjustments
Kilpartick, Swafford, & Findell (2001) revealed that students needed to make many adjustments in the transition from arithmetic to algebra even for excellent students in arithmetic. The assumption was supported by many examples provided by their analysis. For example, an adjustment from answers orientation to relations orientation was illustrated from the following statement “elementary school arithmetic tends to be heavily answer- oriented and does not focus on the representation of relations” (p. 261). A specific example provided by them was that students always assumed ![]() as a computing signal and typically wrote 13 for the number sentence
as a computing signal and typically wrote 13 for the number sentence ![]() by evaluating it instead of the correct answer 4. Another adjustment from undoing operation to expressing equation was exemplified by a problem solving “when 3 is added to 5 times a certain number, the sum is 38; find the number” (p. 262). The arithmetic method is undoing in reverse order (subtract 3 from 38 and then divide by 5), while algebraic way is to represent the relationships by the stated operation:
by evaluating it instead of the correct answer 4. Another adjustment from undoing operation to expressing equation was exemplified by a problem solving “when 3 is added to 5 times a certain number, the sum is 38; find the number” (p. 262). The arithmetic method is undoing in reverse order (subtract 3 from 38 and then divide by 5), while algebraic way is to represent the relationships by the stated operation:![]() . Therefore, the different methods require the students to make certain adjustments.
. Therefore, the different methods require the students to make certain adjustments.
Based on the idea of adjustments, Kieran (2004: pp. 140-141) defined five kinds of adjustments: 1) a focus on relations and not merely on the calculation of a numerical answer; 2) a focus on operations as well as their inverses, and on the related idea of doing/undoing; 3) a focus on both representing and solving a problem rather than on merely solving it; 4) a focus on both numbers and letters, rather than on numbers alone including: working with letters that may at times be unknowns, variables, or parameters; accepting unclosed literal expressions as responses; comparing expressions for equivalence based on properties rather than on numerical evaluation; and 5) a refocusing of the meaning of the equal sign. The five adjustments are not only the knowledge we should know about students’ transition from arithmetic to algebra but also the guidance for teaching to prevent or treat students’ difficulties in algebra learning.
In fact, the transition knowledge generated from the literature is taken as the systemization of main challenges students might encounter and the suggestions of overcoming their difficulties in the algebra learning. Therefore, the knowledge is also regarded as a remedy for the scarcity of teaching orientation.
7. Conclusions
In this literature review, it is attempted to re-conceptualize much of the existing algebra researches by focusing on the challenges that students might confront with in learning algebra from the perspectives of algebra content, cognitive gap, teaching issues, learning matters, and transition knowledge. The perspectives adopted in this paper could serve as a framework of better understanding students’ difficulties in their algebra learning.
In addition, from the critical perspective of reviewing the existing researches, it could be found that the existing researches are conducted from the static angle to examine the causes resulting in students’ difficulties in algebra learning. In another word, there is a lack of process analysis of students’ going through the transition from arithmetic to algebra. Without the undoing of the process, we could not perceive the circumstances that the students could struggle with so well that we could not provide apt strategies to prevent or remedy the difficulties (Wang, 2014: p. 2) in a systemic way even though we know the existing difficulties and their causes.
Fund
The Research Fund of Humanities and Social Science of the Ministry of Education, China (13YJC880075).