Schur Complement Computations in Intel® Math Kernel Library PARDISO ()
1. Introduction
According to F. Zhang [1] , the term “Schur complement” was used first by E. Haynsworth [2] . Haynsworth chose this term because of the lemma (Schur determinant lemma) in the paper [3] that was edited by Schur himself. In spite of matrix 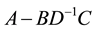 being used in this lemma as a secondary term, later this matrix came to play an important role in mathematical algorithms as the Schur complement. It is denoted as
being used in this lemma as a secondary term, later this matrix came to play an important role in mathematical algorithms as the Schur complement. It is denoted as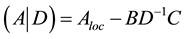 . For example, in mathematical statistics, the Schur complement matrix is important in computation of the probability density function of multivariate normal distribution, and in computational mechanics the Schur complement matrix correlates to media stiffness.
. For example, in mathematical statistics, the Schur complement matrix is important in computation of the probability density function of multivariate normal distribution, and in computational mechanics the Schur complement matrix correlates to media stiffness.
Partial solving of systems of linear equations plays an important role in linear algebra for implementation of efficient preconditioners based on domain decomposition algorithms. Partial solutions usually involve sparse matrices. For this reason Schur complement computations and partial solving have been implemented in Intel® Math Kernel Library (Intel® MKL) [4] . This paper covers the ideas behind the implementation.
There are a number of papers that focused on efficient implementation of the Schur complement. As example, Aleksandrov and Samuel [5] in their paper proposed algorithm to calcluate the Schur complement for Sparse system. Yamazaki and Li published an idea [6] of how to implement Schur complement efficiently on cluster. And we need to mention MUMPS solver [7] that integrated the Schur complement computation a few years ago.
Intel® MKL PARDISO [4] can be considered as one of the multifrontal methods that have been proposed by Duff [8] and further expanded by Liu [9] . This method is divided into three stages. First, the initial matrix undergoes a reordering procedure like the one developed by Karypis [10] [11] in order to represent it in the form of a dependency tree. Then symbolic factorization takes place, where the total number of nonzero elements is computed in LDU decomposition. And finally, factorization of the permuted matrix in the LDU form is performed like the factorization proposed in Amestoy [12] -[16] . In the last stage, both forward and backward substitutions are implemented to compute a solution for the two triangular systems.
The proposed implementation of the Schur complement continues the work of the authors in the area of multifrontal direct sparse solvers. In Kalinkin [17] , the basic algorithm was implemented for symmetric, positive definite matrices. In the presentations [18] and [19] , the proposed algorithm was significantly improved by balancing the dependency tree. In [20] , the algorithm was expanded to non-positive definite matrices and non- symmetric matrices. In this paper, we propose to move all matrix elements that correlate to Schur complement to the top of the dependency tree in order to improve parallelization of computations.
Let A be a symmetric positive definite sparse matrix (the symmetry and positive definiteness of the matrix is set in order to simplify the algorithm description avoiding the case of degenerate matrix minors):
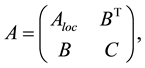 (1)
(1)
where 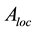 and C are square sparse positive definite matrices, and B is a sparse rectangular matrix. Then we can make the following decomposition, which is similar to a Cholesky decomposition of matrix A:
and C are square sparse positive definite matrices, and B is a sparse rectangular matrix. Then we can make the following decomposition, which is similar to a Cholesky decomposition of matrix A:
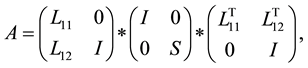 (2)
(2)
where
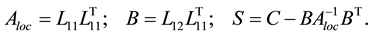
The matrix 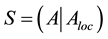 is the Schur complement. The general approach to computing the Schur complement based on this formula and mathematical kernels can be expressed in the form of pseudocode:
is the Schur complement. The general approach to computing the Schur complement based on this formula and mathematical kernels can be expressed in the form of pseudocode:
![]()
Algorithm 1.Simple Schur complement computational algorithm.
This algorithm has several significant disadvantages that can form barriers for its implementation for large sparse systems. The main disadvantage is in the step 2 of Algorithm 1 involving the conversion of sparse matrix BT into a dense matrix, which requires allocating a lot of memory for storing temporary data. Also, if we consider BT as a dense matrix a large number of zero elements are processed in multiplication 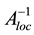 BT, which would make this step one of the most computational intensive parts of the algorithm and would significantly increase the overall computational time. To prevent this, we propose the following algorithm based on the multifrontal approach which calculates the Schur complement matrix first, and then the factorization of the matrix A without significant memory requirements for the computations to proceed.
BT, which would make this step one of the most computational intensive parts of the algorithm and would significantly increase the overall computational time. To prevent this, we propose the following algorithm based on the multifrontal approach which calculates the Schur complement matrix first, and then the factorization of the matrix A without significant memory requirements for the computations to proceed.
2. Schur Complement Computational Algorithm
As in the papers [17] -[20] , consider a sparse symmetric matrix Aloc as in the left of Figure 1, where each shaded block is a sparse sub-matrix and each white block is a zero sub-matrix. Using reordering algorithm procedures [10] [11] , this matrix can be rotated to the pattern shown in the right of Figure 1. A reordered matrix is more convenient for computations than the initial one since Cholesky decomposition can start simultaneously from several entry points (for the matrix on the right of Figure 1, the first, second, fourth, and fifth rows of the matrix L can be calculated independently.
Let us append the original matrix Aloc stored in the sparse format with zeroes so that its nonzero pattern matches completely that of the matrix L. The elements of L in row 3 can be computed only after the elements in rows 1 and 2 are computed; similarly, element in row 6 can be computed only after elements in rows 4 and 5 are computed. The elements in the 7th row can be computed last. This allows us to construct the dependency tree [10] [11] : a graph, where each node corresponds to a single row of the matrix and each graph node can be computed only if its children (nodes on which it depends) are computed. A deeper discussion of the algorithm with pseudocode of the distribution of nodes of the tree between processes can be found in [17] . The dependency tree for the matrix is given in Figure 2 (the number in the center of a node shows the row number).
Such a representation allows us to modify Algorithm 1 using the following notation: node Zj is a child of Zi if Zj resides lower than Zi in the dependency tree (Figure 2) and there is a connection from Zj to Zi.
![]()
Algorithm 2. LLT decomposition based on the dependency tree.
where by maskiZj we denote a submatrix built as intersection of columns corresponding to node Zi with rows corresponding to node Zj. In terms of representation in the right of the Figure 1 that would mean the ij-th square.
To calculate the Schur complement let us add to the representation in the columns and rows of matrices B, BT, and C to achieve full representation of matrix A as in left part of the Figure 3. As one can see, we achieve similar representation to the Figure 2 with additional rows corresponding to those of matrices B and C in Figure 3
![]()
![]()
Figure 1. Nonzero pattern of the original matrix (left) and of the same matrix after reordering (right).
![]()
![]()
Figure 3. Nonzero pattern of matrix A after reordering of Aloc (left) and its tree representation (right).
(right). Note that blocks corresponding to the columns and rows of matrices BT, B, and C are sparse. After factorization of the full matrix A the number of nonzero elements there increases significantly, but our experiments show that the blocks remain sparse and do not become dense.
Let’s introduce the following notation: 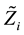 is Zi node of the tree expanded by the corresponding rows of the matrix BT, ZC is a node of the tree corresponding to the matrix C. Then we can modify Algorithm 2 to take into account the elements of matrices B, BT, and C.
is Zi node of the tree expanded by the corresponding rows of the matrix BT, ZC is a node of the tree corresponding to the matrix C. Then we can modify Algorithm 2 to take into account the elements of matrices B, BT, and C.
This algorithm produces![]() . In fact, the Algorithm 3 fully corresponds to the simple Algorithm 2 without calculations of the LLT decomposition of the last submatrix.
. In fact, the Algorithm 3 fully corresponds to the simple Algorithm 2 without calculations of the LLT decomposition of the last submatrix.
The approach proposed can be implemented on a parallel computers with a small modification of Algorithm 3.
Approach presented in Algorithm 4 allows us to implement the Schur complement of sparse matrix in Intel® Math Kernel Library.
3. Experiments
For all experiments we used a compute node with two Intel® Xeon® processors E5-2697 v3 (35MB cache, 2.60 GHz) with 64GB RAM, MUMPS version 4.10.0 [7] , Intel MKL 11.2 Update 1 [4] .
Figure 4 shows a cubic domain in which we apply seven-point approximation for a Laplace operator with mesh size ![]() to generate matrix A, and its cut-off through one of the axes as a domain for which we want to calculate the Schur complement (Figure 4 (left)).
to generate matrix A, and its cut-off through one of the axes as a domain for which we want to calculate the Schur complement (Figure 4 (left)).
Figure 4 shows the portrait of matrix A before factorization (center) and the portrait of matrix L after factorization (right). One can see that the sparsity of L in the Schur complement columns decreased versus the sparsity of the part of L that corresponds to matrix Aloc, though it stays sparse and overall the number of nonzero elements increases slightly. For this test, we see that the number of nonzero elements is only five percent higher in the case when we calculate the Schur complement (Algorithm 3) compared to the case without Schur complement calculations (straight factorization).
In Figure 5 and Figure 6 we compare the performance of the implemented functionality with the similar functionality provided by the MUMPS package [7] . We compare the time needed to compute Schur complement matrix and return it in the dense format. The last 5000 rows and columns of the matrices presented are chosen for Schur complement computations.
For Figure 5 we chose 2 matrices from Florida Matrix collection [21] : Fault_639 with about 600 K rows and columns and 27 M nonzero elements, and Serena with 1.3 M rows and columns and 64 M nonzero elements. On the x axis we plotted the number of threads on the compute node used for computation of the Schur complement. One can see that the time for computing Schur complement is almost the same for a small number of threads, but the time needed for Intel MKL PARDISO solver decreases when the number of threads increases.
For Figure 6 we chose 2 matricesfrom Florida Matrix collection [21] : Geo_1438 with about 1.4 M rows and columns and 602 M nonzero elements, and Flan_1565 with 1.5 M rows and columns and 114 M nonzero elements. As before, on the x axis we plotted the number of threads on the compute node used for computation of the Schur complement. Notice that overall picture does not change significantly. The main difference between this set of matrices and the previous one is in sparsity―average number of nonzero elements per row. In the first set of experiments (Fault_639 and Serena) we used sparse matrices with fewer than 50 nonzero elements per
![]()
![]()
![]()
Figure 4. A domain with a dividing plane corresponding to Schur submatrix (left), portraits of the matrix before (center) and after factorization (right).
![]() Performance tests and ratings are measured using specific computer systems and/or components and reflect the approximate performance of Intel products as measured by those tests. Any difference in system hardware or software design or configuration may affect actual performance. Buyers should consult other sources of information to evaluate the performance of systems or components they are considering purchasing. For more information on performance tests and on the performance of Intel products, refer to http://www.intel.com/content/www/us/en/benchmarks/resources-benchmark-limitations.html Refer to our Optimization Notice for more information regarding performance and optimization choices in Intel software products at: http://software.intel.com/enru/articles/optimization-notice/
Performance tests and ratings are measured using specific computer systems and/or components and reflect the approximate performance of Intel products as measured by those tests. Any difference in system hardware or software design or configuration may affect actual performance. Buyers should consult other sources of information to evaluate the performance of systems or components they are considering purchasing. For more information on performance tests and on the performance of Intel products, refer to http://www.intel.com/content/www/us/en/benchmarks/resources-benchmark-limitations.html Refer to our Optimization Notice for more information regarding performance and optimization choices in Intel software products at: http://software.intel.com/enru/articles/optimization-notice/
Figure 5. Schur complement computational time for matrices Fault 639 and Serena with Intel MKL PARDISO and MUMPS.
![]() Performance tests and ratings are measured using specific computer systems and/or components and reflect the approximate performance of Intel products as measured by those tests. Any difference in system hardware or software design or configuration may affect actual performance. Buyers should consult other sources of information to evaluate the performance of systems or components they are considering purchasing. For more information on performance tests and on the performance of Intel products, refer to http://www.intel.com/content/www/us/en/benchmarks/resources-benchmark-limitations.html Refer to our Optimization Notice for more information regarding performance and optimization choices in Intel software products at: http://software.intel.com/enru/articles/optimization-notice/
Performance tests and ratings are measured using specific computer systems and/or components and reflect the approximate performance of Intel products as measured by those tests. Any difference in system hardware or software design or configuration may affect actual performance. Buyers should consult other sources of information to evaluate the performance of systems or components they are considering purchasing. For more information on performance tests and on the performance of Intel products, refer to http://www.intel.com/content/www/us/en/benchmarks/resources-benchmark-limitations.html Refer to our Optimization Notice for more information regarding performance and optimization choices in Intel software products at: http://software.intel.com/enru/articles/optimization-notice/
Figure 6.Schur complement computational time for matrices Geo 1438 and Flan 1565 with Intel® MKL PARDISO and MUMPS.
row on average, while the sparsity of Flan_1565 is about 70 nonzero elements per row and the sparsity of Geo_1438 is more than 400 nonzero elements per row. In both cases the time for Schur complement computations is almost the same when the number of threads is small for the Intel MKL and MUMPS, but the time needed for Intel MKL PARDISO solver significantly decreases when the number of threads increases. Moreover, comparison of Figure 5 and Figure 6 indicates that the performance of Intel MKL PARDISO becomes better if sparsity increases.
4. Conclusion
We demonstrated an approach that calculates the Schur complement for a sparse matrix implemented in Intel Math Kernel Library using the Intel MKL PARDISO interface. This implementation allows one to use a Schur complement for sparse matrices appearing in various mathematical applications, from statistical analysis to algebraic solvers. The proposed approach shows good scalability in terms of computational time and better performance than similar approaches proposed elsewhere.