1. Introduction
In many instances, the type of data available for modeling and that used for optimization is a set of observations measured over time of system variable(s) of interest [1] -[4] . A time series stated as only one realization of a stochastic process is a set of data measured through time. In many areas from engineering to economics, patterns of time series are encountered. It is difficult to find a science program not required to study with a data set in form of time series. The characteristic property of a time series is that its future behavior can not be exactly estimated. It is not uncommon in economic analysis to develop a model and perform empirical analysis by assuming that economic agents make decisions based on a set of available information [5] . In empirical analyses, however, the information is usually designated by a generic information set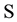 . There is no attempt to quantify the amount of information in
. There is no attempt to quantify the amount of information in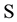 . A quantification of the worth of such a set would not be an easy task even if one could identify all elements of
. A quantification of the worth of such a set would not be an easy task even if one could identify all elements of 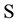 [6] . In this paper, we view the flow of information to a stochastic process from the autocovariance sets and consider measuring the amount of information when
[6] . In this paper, we view the flow of information to a stochastic process from the autocovariance sets and consider measuring the amount of information when 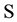 is a set which consists of autocovariances obtained from the time series. For this reason, it is concerned with the analysis of the ordered data using the principle of maximum entropy when the information about the times series is given by autocovariances up to a lag m. According to the maximum entropy approach, given time series can be viewed as single trial from a stochastic process that is stationary up to its second-order statistics and has a zero mean. It is known that MaxEnt distribution of an observed time series is determined as a multivariate normal distribution whose dimension is equal to the number of observations [1] . By virtue of the entropy of normal distribution, entropy optimization (EO) functional is constructed as Hmax. It can be shown that as the number of constraints generated by autocovariances increases, value of Hmax decreases. In this investigation, firstly MaxEnt distribution for stationary time series subject to constraints generated by autocovariances set
is a set which consists of autocovariances obtained from the time series. For this reason, it is concerned with the analysis of the ordered data using the principle of maximum entropy when the information about the times series is given by autocovariances up to a lag m. According to the maximum entropy approach, given time series can be viewed as single trial from a stochastic process that is stationary up to its second-order statistics and has a zero mean. It is known that MaxEnt distribution of an observed time series is determined as a multivariate normal distribution whose dimension is equal to the number of observations [1] . By virtue of the entropy of normal distribution, entropy optimization (EO) functional is constructed as Hmax. It can be shown that as the number of constraints generated by autocovariances increases, value of Hmax decreases. In this investigation, firstly MaxEnt distribution for stationary time series subject to constraints generated by autocovariances set 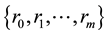 is considered. It is proved that as number of lags of successive autocovariances increases, the entropy value of this distribution goes on decreasing but its information worth goes on increasing. Furthermore, by starting from MaxEnt distribution dependent on parameters, MinMaxEnt distribution which has minimum entropy and maximum information out of all MaxEnt distributions is defined. It should be noted that MinMaxEnt and MaxMaxEnt distributions as solutions of Generalized Entropy Optimization (GEO) problem firstly are defined and generally investigated in [7] -[9] . In [10] , GEO distribution dependent on parameters in time series is introduced and via this distribution an estimation method of missing value is proposed. In this study, it is shown that entropy value and information worth of MinMaxEnt distribution obtained on the bases of MaxEnt distribution dependent on parameters has the same above expressed properties at each fixed value of parameters as MaxEnt distribution. In addition, it is proved that information worth of each model defined on the basis of MinMaxEnt modeling about stationary time series is equal to the sum of all possible information increments corresponding to each model with respect to preceding model starting with first model in the sequence of models. The fulfillment of obtained results is demonstrated on an example by the use of a program written in Matlab.
is considered. It is proved that as number of lags of successive autocovariances increases, the entropy value of this distribution goes on decreasing but its information worth goes on increasing. Furthermore, by starting from MaxEnt distribution dependent on parameters, MinMaxEnt distribution which has minimum entropy and maximum information out of all MaxEnt distributions is defined. It should be noted that MinMaxEnt and MaxMaxEnt distributions as solutions of Generalized Entropy Optimization (GEO) problem firstly are defined and generally investigated in [7] -[9] . In [10] , GEO distribution dependent on parameters in time series is introduced and via this distribution an estimation method of missing value is proposed. In this study, it is shown that entropy value and information worth of MinMaxEnt distribution obtained on the bases of MaxEnt distribution dependent on parameters has the same above expressed properties at each fixed value of parameters as MaxEnt distribution. In addition, it is proved that information worth of each model defined on the basis of MinMaxEnt modeling about stationary time series is equal to the sum of all possible information increments corresponding to each model with respect to preceding model starting with first model in the sequence of models. The fulfillment of obtained results is demonstrated on an example by the use of a program written in Matlab.
2. Information Worth of Autocovariances Set in MaxEnt Modeling
In this section, MaxEnt distributions according to different number of autocovariances are considered and it is proved that the entropy values of these distributions constitute a monotonically decreasing sequence when the number of autocovariances increases. Moreover it is shown that the information generated by autocovariances set is expressed as sum of information worth of each autocovariance taken separately.
Theorem 1. Let 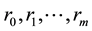 be autocovariances with
be autocovariances with 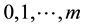 lags of observed stationary time series
lags of observed stationary time series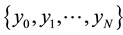 ,
, 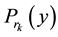 be MaxEnt distribution subject to constraints generated by autocovariances set
be MaxEnt distribution subject to constraints generated by autocovariances set 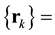
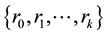 ,
,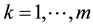 ; m < N and
; m < N and 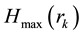 be the entropy value of this distribution. Then, entropy values of mentioned MaxEnt distributions form a monotonically decreasing sequence of the following form:
be the entropy value of this distribution. Then, entropy values of mentioned MaxEnt distributions form a monotonically decreasing sequence of the following form:
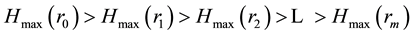 (1)
(1)
Proof. The Shannon entropy measure subject to constraints generated by autocovariances 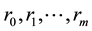 with
with 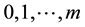 of stationary time series
of stationary time series ![]() is multivariate normal [1] . Therefore by increasing of the number of k of autocovariances vector
is multivariate normal [1] . Therefore by increasing of the number of k of autocovariances vector![]() , the conditions to maximize Shannon measure is increased and the domain of entropy measure becomes narrow. Consequently, entropy value of
, the conditions to maximize Shannon measure is increased and the domain of entropy measure becomes narrow. Consequently, entropy value of ![]() is strongly decreased and the inequalities (1) are satisfied. Theorem 1 is proved.
is strongly decreased and the inequalities (1) are satisfied. Theorem 1 is proved.
If we denote by ![]() information worth of autocovariance rk, due to the fact that the information discrepancy between two distributions is measured in terms of their entropy difference in MaxEnt modeling, then
information worth of autocovariance rk, due to the fact that the information discrepancy between two distributions is measured in terms of their entropy difference in MaxEnt modeling, then
![]() (2)
(2)
Furthermore, if information worth generated by autocovariances set ![]() in the aggregate is denoted by
in the aggregate is denoted by![]() ,
, ![]() , then
, then
![]() (3)
(3)
Remark 1. The information![]() ,
, ![]() , generated by autocovariances set
, generated by autocovariances set ![]() is expressed as sum of information worths of each autocovariances taken separately,
is expressed as sum of information worths of each autocovariances taken separately,
![]() (4)
(4)
From (3) by virtue of formula (2) follows
![]()
consequently
![]()
3. Information Worth of Dependent on Parameters
In this section, according to different number of autocovariances MaxEnt distributions dependent on parameters are considered and it is proved that at each value of parameter, these distributions and their entropies possess the same properties as in section 2.
Theorem 2. Let ![]() be MaxEnt distribution generated by autocovariances set
be MaxEnt distribution generated by autocovariances set ![]() of given stationary time series
of given stationary time series ![]() with missing value
with missing value![]() , where
, where![]() ,
,![]() . Since
. Since ![]() depend on
depend on![]() , MaxEnt distribution
, MaxEnt distribution ![]() is also dependent on
is also dependent on![]() . Thereafter, autocovariances set
. Thereafter, autocovariances set ![]() will be represented as
will be represented as![]() , MaxEnt distribution as
, MaxEnt distribution as ![]() and entropy of this distribution as
and entropy of this distribution as![]() . Thus, we have a family of time series dependent on
. Thus, we have a family of time series dependent on![]() .
.
Between entropy values ![]() of MaxEnt distributions
of MaxEnt distributions![]() ,
, ![]() the following inequalities are fulfilled:
the following inequalities are fulfilled:
![]() (5)
(5)
In other words, entropy values of MaxEnt distributions dependent on ![]() constitute a monotonically decreasing sequence.
constitute a monotonically decreasing sequence.
Proof. According to Theorem 1, entropy values ![]() of MaxEnt distributions form a monotonically decreasing sequence of the form (1). Since
of MaxEnt distributions form a monotonically decreasing sequence of the form (1). Since ![]() depend on
depend on![]() . Consequently, inequalities (5) are satisfied. Theorem 2 is proved.
. Consequently, inequalities (5) are satisfied. Theorem 2 is proved.
Information worth ![]() of autocovariance rk dependent on
of autocovariance rk dependent on ![]() is determined by the following equation similarly to (2),
is determined by the following equation similarly to (2),
![]() (6)
(6)
Then, information worth generated by autocovariances set ![]() is denoted by
is denoted by ![]() ,
, ![]() , and
, and
![]() (7)
(7)
Remark 2. The information![]() ,
, ![]() , generated by autocovariances set
, generated by autocovariances set ![]() is expressed as sum of information worths of each autocovariances taken separately,
is expressed as sum of information worths of each autocovariances taken separately,
![]() (8)
(8)
From (7) by virtue of formula (6) follows
![]()
![]()
4. Information Worth of MinMaxEnt Models Dependent on Autocovariances
In this section, MinMaxEnt distributions (models) are obtained on the basis of MaxEnt distributions dependent on parameters and it is shown that as the number of autocovariances k goes on increasing, the entropy of approximating distribution (model) goes on decreasing. Furthermore, it is proved that information worth of each model defined on the basis of MinMaxEnt modeling about stationary time series is equal to the sum of all possible information increments corresponding to each model with respect to preceding model starting with first model in the sequence of models.
Theorem 3. Let ![]() be MaxEnt distribution generated by autocovariances set
be MaxEnt distribution generated by autocovariances set ![]() of given stationary time series
of given stationary time series ![]() with parameter
with parameter![]() , at position s, where
, at position s, where![]() ,
, ![]() and entropy value of this distribution be
and entropy value of this distribution be![]() . Moreover, let
. Moreover, let![]() ,
, ![]() be the value
be the value ![]() realizing MinMaxEnt distribution
realizing MinMaxEnt distribution![]() , in other words
, in other words
![]() (9)
(9)
Then, between entropy values of MinMaxEnt distributions the inequalities
![]() (10)
(10)
are satisfied.
Proof. According to Theorem 2 for any![]() ,
, ![]() , the inequalities (5) hold. For this reason,
, the inequalities (5) hold. For this reason,
![]() (11)
(11)
On the other hand,
![]() (12)
(12)
![]() (13)
(13)
From inequality (11) by taken into account (12) and (13), the inequality
![]() (14)
(14)
is got. If this process is consecutively repeated, then it is easy to get to the inequalities (10). Theorem 3 is proved.
Remark 3. By using Theorem 3, it is possible to obtain information worth of MinMaxEnt distributions with the different number of autocovariances.
By using Theorem 3, it is possible to obtain information worth of MinMaxEnt distributions with the different number of autocovariances. However, in order to simplify the description of results, we introduce the following symbols. Let![]() ,
, ![]() be a model representing MinMaxEnt distribution
be a model representing MinMaxEnt distribution ![]() for a stationary time series
for a stationary time series![]() . Moreover, let
. Moreover, let![]() ,
, ![]() be the information contained by model
be the information contained by model ![]() about this time series, then
about this time series, then
![]() (15)
(15)
and
![]() (16)
(16)
From (15) and (16),
![]()
![]() (17)
(17)
where ![]() is the information increment corresponding to each model
is the information increment corresponding to each model ![]() with respect to preceding model
with respect to preceding model![]() . By virtue of the obtained results, the following theorem can be asserted.
. By virtue of the obtained results, the following theorem can be asserted.
Theorem 4. Information worth ![]() of model Ym defined on the basis of MinMaxEnt modelling about stationary time series
of model Ym defined on the basis of MinMaxEnt modelling about stationary time series ![]() is equal to sum of all possible information increments
is equal to sum of all possible information increments ![]() ,
, ![]() corresponding to each model with respect to preceding model
corresponding to each model with respect to preceding model ![]() starting with first model
starting with first model ![]() in the sequence of models
in the sequence of models![]() .
.
Proof. By using the new notations ![]() inequalities (10) can be represented as
inequalities (10) can be represented as
![]() (18)
(18)
Equation (10) shows that as the number of autocovariances k increases, the entropy of approximating distribution (model) goes on decreasing but it never goes below the entropy of probability distribution satisfying the same conditions as MinMaxEnt distribution. According to (15) and (17)
![]()
or
![]() (19)
(19)
According to (18) in (19), ![]() ,
,![]() . Theorem 4 is proved.
. Theorem 4 is proved.
5. Applications
The developed MinMaxEnt models ![]() can be applied to estimate the missing value in time series. According to Theorem 4, information worth generated by
can be applied to estimate the missing value in time series. According to Theorem 4, information worth generated by ![]() is greater than information worth generated by
is greater than information worth generated by![]() . Consequently,
. Consequently, ![]() generating the model
generating the model ![]() is the better estimation than
is the better estimation than ![]() generating the model
generating the model ![]() in the sense of information worth. On an example it is shown that mentioned estimated value is the best also in the sense of mean square error (MSE). To realize required operations, a program in MATLAB is written. For this purpose, we have considered data set generated from autoregressive process
in the sense of information worth. On an example it is shown that mentioned estimated value is the best also in the sense of mean square error (MSE). To realize required operations, a program in MATLAB is written. For this purpose, we have considered data set generated from autoregressive process ![]() as follows:
as follows:
![]() (20)
(20)
and the data set is given in Table 1. By using the data in Table 1, estimations based on MinMaxEnt models are obtained for missing values in each position via constraints generated by ![]() autocovariances and
autocovariances and ![]() autocovariances. From Table 1 it is seen that, MinMaxEnt estimations
autocovariances. From Table 1 it is seen that, MinMaxEnt estimations ![]() determined by the set consisting of
determined by the set consisting of ![]() autocovariances are better than MinMaxEnt estimations
autocovariances are better than MinMaxEnt estimations ![]() determined by the set consisting of
determined by the set consisting of ![]() autocovariances in each position. Moreover,
autocovariances in each position. Moreover, ![]() calculated by MinMaxEnt
calculated by MinMaxEnt
estimations with autocovariances is 0.2564 and it is lower than ![]() calculated by MinMax-
calculated by MinMax-
Ent estimations with ![]() autocovariances and
autocovariances and ![]() calculated by MinMaxEnt estimations with
calculated by MinMaxEnt estimations with ![]() autocovariances.
autocovariances.
Furthermore, in Table 2 the entropy and information worth of different autocovariance sets are given. These quantities calculated from the data set verify Theorem 4. It can be seen that as the number of constraints which is generated by autocovariances increases, the value of Hmax decreases.
![]()
Table 1. The data generated from AR(4) and its estimations with different autocovariance sets.
![]()
Table 2. Entropy and information worth of different autocovariance sets.
6. Conclusions
In this study, the following results are established.
・ MaxEnt distributions according to different number of autocovariances are considered and it is proved that the entropy values of these distributions constitute a monotonically decreasing sequence when the number of autocovariances increases. Moreover it is shown that the information generated by autocovariances set is expressed as sum of information worth of each autocovariance taken separately.
・ According to different number of autocovariances, MaxEnt distributions dependent on parameters are considered and it is proved that at each value of parameter these distributions and their entropies possess the same properties as the MaxEnt distributions.
・ MinMaxEnt distributions (models) are obtained on the basis of MaxEnt distributions dependent on parameters and it is shown that as the number of autocovariances k goes on increasing, the entropy of approximating distribution (model) goes on decreasing. Furthermore, it is proved that information worth of each model defined on the basis of MinMaxEnt modeling about stationary time series is equal to the sum of all possible information increments corresponding to each model with respect to preceding model starting with first model in the sequence of models.
・ Information worth of autocovariances in time series and values generating MinMaxEnt distributions can be applied in solving many problems. One of the mentioned problems is the problem of estimation of missing value in time series. It is proved that the value generating MinMaxEnt distribution independence on position represents the best estimation of the missing value in the sense of information worth.
・ The fulfillment of the obtained results is demonstrated on an example by using a program written in Matlab.
Acknowledgements
We thank the Editor and the referee for their comments. This support is greatly appreciated.