1. Introduction
Strictly monotonic sequences do not assume their limit. Rarely the terms of the sequence and its limit are confused. But this situation changes dramatically when sequences of partial sums of series are involved. It is customary in textbooks to identify the infinite sum over all terms of a series and the limit of this series [1] , often called its “sum”. G. Cantor, one of the inventors of this habit, wrote: “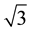 ist also nur ein Zeichen für eine Zahl, welche erst noch gefunden werden soll, nicht aber deren Definition. Letztere wird jedoch in meiner Weise etwa durch (1.7, 1.73, 1.732, ...) befriedigend gegeben.” [2]
ist also nur ein Zeichen für eine Zahl, welche erst noch gefunden werden soll, nicht aber deren Definition. Letztere wird jedoch in meiner Weise etwa durch (1.7, 1.73, 1.732, ...) befriedigend gegeben.” [2] 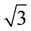 is only a symbol for a number which has yet to be found, but is not its definition. The number itself however is given satisfactorily in my way by (1.7, 1.73, 1.732, …).
is only a symbol for a number which has yet to be found, but is not its definition. The number itself however is given satisfactorily in my way by (1.7, 1.73, 1.732, …).
In the following we will see that this is imprecise and point out an important consequence. A limit is not defined by the infinite sequence of partial sums because the sequence cannot be given in the necessary completeness. Only a finite formula can determine both the terms of the sequence of partial sums and the limit as well.
2. Theorem and Proof
Theorem A non-terminating series of decimal fractions does not determine a real number.
Corollary A non-terminating digit sequence does not determine a real number.
Proof. The limit of a strictly monotonic sequence is not among its terms. Strictly monotonic sequences like
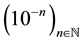 or
or 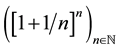 or
or 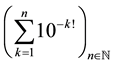 sufficiently show this. None of the
sufficiently show this. None of the 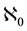 indexed terms is equal to the limit 0, e, and Liouville’s number L, respectively. (
indexed terms is equal to the limit 0, e, and Liouville’s number L, respectively. (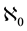 is the cardinality of the set
is the cardinality of the set 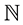 of natural numbers n.)
of natural numbers n.)
The same distinction has to be observed with series. There must not be a difference in the mathematical contents whether the partial sums are written separately like
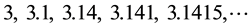 (1)
(1)
or are written in one line with interruptions
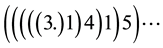 (2)
(2)
or without interruptions
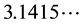 (3)
(3)
The infinite sequence of digits dn is completely exhausted by all terms of the Cauchy-sequence of rational partial sums of decimal fractions. The intended meaning as a sequence of rational partial sums according to Eq-
uation (1) can be expressed also by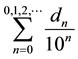 . Equation (3) giving the infinite sum
. Equation (3) giving the infinite sum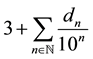 , is merely an
, is merely an
abbreviation: All partial sums are written in one and the same line without adding the limit. Equation (2) is the same because writing or not writing parentheses must not change the result. In all cases none of the 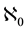 decimal fractions is left out. The “sum” of the series, i.e., the limit of the Cauchy-sequence of partial sums, is not established by any term with natural index
decimal fractions is left out. The “sum” of the series, i.e., the limit of the Cauchy-sequence of partial sums, is not established by any term with natural index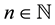 . But only all these
. But only all these 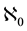 terms are given in Equations (1) to (3) as well as on the left-hand sides of the following examples whereas the limits are given on the right-hand sides.
terms are given in Equations (1) to (3) as well as on the left-hand sides of the following examples whereas the limits are given on the right-hand sides.
![]()
Digits are simply too coarse-grained to represent irrational limits of Cauchy-sequences.
To represent ![]() by an infinite digit sequence, we would need infinitely many digits 0 preceding the digit 1. Whereas it is obvious that this is impossible, the infinitely many digits 1 required for the expansion of
by an infinite digit sequence, we would need infinitely many digits 0 preceding the digit 1. Whereas it is obvious that this is impossible, the infinitely many digits 1 required for the expansion of ![]() are usually swallowed without scruples. But it is as obvious that digits 0 and digits 1 do not allow for a different treatment with respect to the fact that never infinitely many can precede one of them.
are usually swallowed without scruples. But it is as obvious that digits 0 and digits 1 do not allow for a different treatment with respect to the fact that never infinitely many can precede one of them.
This leads us to the often asserted double-representation of periodic rational numbers. For all ![]() the sum of the nth terms of the two complementary sequences
the sum of the nth terms of the two complementary sequences
![]()
is 1. Since all ![]() digits are not sufficient to realize the limit 0 of the first sequence, all
digits are not sufficient to realize the limit 0 of the first sequence, all ![]() digits of 0.999… are not sufficient to realize the limit 1 of the second sequence. Only when explicitly taking the limits of the sequences, we get 0 and 1, respectively. For series, taking the limit is usually assumed without saying and does not cause mistakes in numerical calculations, but if we look at the matter with advisable mathematical precision, we see
digits of 0.999… are not sufficient to realize the limit 1 of the second sequence. Only when explicitly taking the limits of the sequences, we get 0 and 1, respectively. For series, taking the limit is usually assumed without saying and does not cause mistakes in numerical calculations, but if we look at the matter with advisable mathematical precision, we see
![]()
The usual proof for![]() , namely
, namely ![]() holds in the limit only. The series 0.999… is not a number but a sequence of partial sums. Like a vector it can be multiplied such that
holds in the limit only. The series 0.999… is not a number but a sequence of partial sums. Like a vector it can be multiplied such that ![]() but it is impossible to isolate one 9 from infinitely many terms.
but it is impossible to isolate one 9 from infinitely many terms.
3. Conclusions
As a result we can state that an infinite digit sequence like![]() , abbreviating an infinite sequence of
, abbreviating an infinite sequence of
partial sums of decimal fractions, also called an infinite series![]() , is not a number (unless
, is not a number (unless
eventually becoming constant). ![]() for example is an abbreviation of the sequence of rational partial sums converging to π. This sequence is purely rational although we cannot find a fraction
for example is an abbreviation of the sequence of rational partial sums converging to π. This sequence is purely rational although we cannot find a fraction ![]() with a common denominator covering all terms of the sequence. This disadvantage however is shared by sequences like
with a common denominator covering all terms of the sequence. This disadvantage however is shared by sequences like ![]() too. We cannot find a fraction with a common denominator covering all terms of the sequences all of which are rational with no doubt.
too. We cannot find a fraction with a common denominator covering all terms of the sequences all of which are rational with no doubt.
A periodic decimal fraction has as its limit a rational number. A non-periodic decimal fraction has as its limit an irrational number. But it is not this number. In case of periodic decimal fractions it is possible, by changing the basis, to obtain a terminating digit sequence. Irrational numbers have no decimal expansion, no representation by digits or bits, not even by infinitely many. They are incommensurable with every rational-measure expanded by digits or bits. An irrational number requires a generating formula F in order to calculate every digit of the infinite digit sequence S and in addition to calculate the limit. The formula F may be interpreted as the number as well as the limit. It may be involved or as simple as “0.111…” which is a finite formula (consisting of eight symbols) allowing to obtain every digit of the infinite sequence converging to 1/9.
The implication ![]() cannot be reversed because without F the sequence S cannot be obtained in the completeness required, i.e., including all its terms such that none is missing.
cannot be reversed because without F the sequence S cannot be obtained in the completeness required, i.e., including all its terms such that none is missing.
4. Consequence
The mathematical facts discussed above also apply to all sequences of digits or bits appearing in the folklore version of Cantor’s diagonal argument [3] or in the binary tree argument [4] . Sequences of digits or bits are never representing irrational numbers, let alone transcendental numbers. Therefore Cantor’s diagonal argument, as well as the binary tree argument, does not concern the cardinality of the set of irrational numbers.