The Gap Labelling Integrated Density of States for a Quasi Crystal Universe Is Identical to the Observed 4.5 Percent Ordinary Energy Density of the Cosmos ()
1. Introduction
It is well known that many models and mathematical techniques that proved to be valuable in the low energy domain of condense matter physics were found to be of considerable usefulness in clarifying basic questions in high energy physics [1] -[7] . Symmetry breaking and phase transition [3] are well known examples for the above, which resulted in the major discovery of the Higgs boson [4] . The hypothesis is also well known that the universe is a gigantic self similar structure [6] [7] as partially evidenced by the planetary system of the Rutherford- Bohr atom model [5] . Nevertheless the result of the present paper goes far beyond what the preceding fact could have led us to believe and it was rather a delightful unexpected result to find that the methods of solid state physics and the suspected self similarity of a fractal universe [6] [7] could lead to accurate results setting the gap labelling integrated density of states for a 3-D quasicrystals [8] - [12] equal to the ordinary energy density of the cosmos as found by COBE, WMAP and the Planck measurements [13] - [18] . In fact these various accurate measurements which lead to several Nobel prizes in physics [13] - [20] are in complete accordance with the theoretical results obtained in the last three years or so [21] - [25] and in turn these theoretical energy density derivations give identical results to the present one [16] - [25] as will be expanded upon in the following sections. In short the main objective of the present paper is to show that the methods of high energy physics and that of low energy solid state physics converge in a clear way leading to the same dark energy density.
2. Integrated Density of States
2.1. Background Information
It is well known that electronic band theory is a very useful and successful theory in the physics of solids that solved difficult problems connected to the design of solar cells and transistors as well as illuminating fundamental properties of solids such as optical absorption and electrical resistance [8] . In this respect the density of states and the Brillouin zone plays a central role [8] . Thus the said density function is defined as the number of electronic states per unit energy for nearby electron energy while the Brillouin zone is polyhedron in Schrö- dinger wave vector space, which is related to a corresponding crystal lattice [8] - [12] .
Now with a somewhat unconventional but well motivated idea in the back of our minds, namely that of draw- ing an instructive analogy between the zero density inside a band gap and the geometry and topology of the crystal lattice on the one side and ordinary energy and dark energy density contained in the structure of our cosmos on the other side, we will start here by extending the above concepts and notions to quasi periodic crystalline [8] [10] [11] . Luckily we already have at our disposal a gap labelling theorem to lean on as well as many results obtained notably by J. Bellisard [8] , A. Connes and many others who applied the powerful mathematical machinery of K-theory and noncommutative geometry [26] to the problem. For example an extensively used standard model is the Fibonacci sequence of two letters a and b in which the frequency of the “a” is given by the golden mean [8] [11] . This we consider next.
2.2. Gap Labelling Density of States of One Dimensional Discrete System
Probably the simplest group of one dimensional systems to illustrate the theory at hand is an automatic sequences such as period doubling, the Rudin-Shapiro sequence and Thue-Morse sequence [8] . However the Fibonacci sequence is the most appropriate for our purpose here not only because it is the simplest but also because it constitutes in the limit a one dimensional Cantorian space with a Hausdorff dimension equal
 and a Menger-Urysohn topological dimension
and a Menger-Urysohn topological dimension 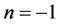 while displaying a remarkable inte-
while displaying a remarkable inte-
grated density of states having the same information as that of a higher dimensional model. Let the two letters alphabet be given by  and let the substitution be
and let the substitution be
 (1)
(1)
Following Bellissard’s general exposition and his notation we find two matrices [8]
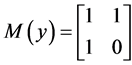 (2)
(2)
and
 (3)
(3)
The largest Eigenvalue of the above is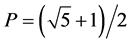 , i.e.
, i.e.  where
where 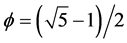 is the golden mean. Using the same notation and abbreviations of [8] the corresponding Eigenvectors are consequently
is the golden mean. Using the same notation and abbreviations of [8] the corresponding Eigenvectors are consequently
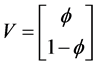
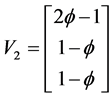 (4)
(4)
and the integrated density of states (IDS) is given by [8]
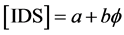 (5)
(5)
where . It is almost impossible for anyone familiar with noncommutative geometry or E-infinity theory to overlook that the preceding density is at a minimum formally identical to that of the compactified Penrose tiling dimensional function [7] [11] [26] as well as the bijection formula of Cantorian spacetime [7] [26] [27] . Thus as simple as the preceding analysis may be, it has far reaching consequences which we discuss next in the context of a K-analysis of the famous Penrose fractal tiling [11] [12] [26] .
. It is almost impossible for anyone familiar with noncommutative geometry or E-infinity theory to overlook that the preceding density is at a minimum formally identical to that of the compactified Penrose tiling dimensional function [7] [11] [26] as well as the bijection formula of Cantorian spacetime [7] [26] [27] . Thus as simple as the preceding analysis may be, it has far reaching consequences which we discuss next in the context of a K-analysis of the famous Penrose fractal tiling [11] [12] [26] .
2.3. Landi’s K-Analysis of the Penrose Tiling
As noted by Landi [12] , the K-theory of Penrose universe treated as x-space by Connes [26] is straight forward and leads via Bratteli diagram and the fact that {0} is the only primitive ideal to the inclusion [12]
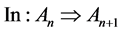 (6)
(6)
which is reminiscent of the previous recursive Fibonacci example. Proceeding in the usual way Landi can then prove the proposition that the c star algebra of the Penrose tiling gives rise to a group given by [12]
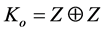 (7)
(7)
and
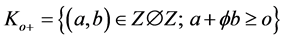 (8)
(8)
This result is again identical to that obtained by Connes and noting the one to one correspondence between the bijection formula of E-infinity Cantorian spacetime [7] [19] [26] - [29]
![]() (9)
(9)
and von Neumann-Connes dimensional function it follows that ko+ as well as [IDS] are simply mathematical tautology, albeit an extremely instructive one bringing various theories for the micro cosmos and the large structure of spacetime [29] to come together and reveal their quintessentially identical nature. One must add however that the bijection formula is a far more compact notation and one could deduce ![]() for negative dimensions much easier than by using the recursive Fibonacci prescription of K-theory and noncommutative geometry. Thus for the empty set we see immediately that
for negative dimensions much easier than by using the recursive Fibonacci prescription of K-theory and noncommutative geometry. Thus for the empty set we see immediately that ![]() leads to [7] [27]
leads to [7] [27]
![]() (10)
(10)
exactly as should be while the zero set is given clearly by [7] [27]
![]() (11)
(11)
so that ![]() is nothing but our unit set [7] [27]
is nothing but our unit set [7] [27]
![]() (12)
(12)
Next we discuss the vital physical and cosmological implication of the preceding results.
3. Ordinary and Dark Energy from Integrated Density of States and Gap Labelling
One of the most important conclusions arrived at from the preceding Section 2 is that what we called topological probability ![]() are also Hausdorff dimensions for negative Menger-Urysohn space [7] [27] and consequently the inverse of a Hausdorff dimension of a corresponding positive dimension n. Actually we have known this fact since a long time from our work on E-infinity [7] [27] . However the slightly new twist is that these normed Hausdorff dimensions or probability corresponds to a subtle form of geometrical density with a physical meaning. To explain what we mean in a more direct and specific way we could do nothing better than derive the celebrated Hardy’s probability for quantum entanglement [19] - [22] and proceed from there to the computation of the ordinary and the dark energy density of our universe and discuss its direct interpretation as an integrated density of states [8] which implies that our cosmos is akin to a gigantic quasi crystalline with Cantorian fine structure.
are also Hausdorff dimensions for negative Menger-Urysohn space [7] [27] and consequently the inverse of a Hausdorff dimension of a corresponding positive dimension n. Actually we have known this fact since a long time from our work on E-infinity [7] [27] . However the slightly new twist is that these normed Hausdorff dimensions or probability corresponds to a subtle form of geometrical density with a physical meaning. To explain what we mean in a more direct and specific way we could do nothing better than derive the celebrated Hardy’s probability for quantum entanglement [19] - [22] and proceed from there to the computation of the ordinary and the dark energy density of our universe and discuss its direct interpretation as an integrated density of states [8] which implies that our cosmos is akin to a gigantic quasi crystalline with Cantorian fine structure.
Hardy’s quantum probability of entanglement [19] - [22] is an ideal starting point for various very good reasons. First it is an exact solution of two quantum particles using orthodox quantum mechanics a la Dirac [19] - [22] . Second this exact solution turned out to be a most surprizing quantitative answer with a strong qualitative flavour being the golden mean ![]() to the power of five, that is to say
to the power of five, that is to say
![]() (13)
(13)
Being a probability we could look upon it as being the inverse of a dimension, i.e. un-normed probability given by the bijection formula [7] [27] . Taking the dimensionality n to be n = 6 one finds [7] [27] [19] - [22]
![]() (14)
(14)
Therefore we have the normed probability [19] - [22]
![]() (15)
(15)
Alternatively we could see P(Hardy) as living in a negative four dimensional space ![]() which leads to [7] [27]
which leads to [7] [27]
![]() (16)
(16)
Here we tacitly made use of the notion of the degree of emptiness of an empty set introduced first by the late inventor of the word fractals, B. Mandelbrot [7] . This is so because the zero set n = 0 is the surface of the empty set ![]() while the empty set
while the empty set ![]() is the surface of an emptier still set
is the surface of an emptier still set![]() . Similarly
. Similarly ![]() is the surface of
is the surface of ![]() and
and ![]() is the surface of
is the surface of ![]() and so on add infinitum until we reach, via the philosophical concept of infinity, the dual philosophical concept of a true insubstantial nothingness [7] [27] .
and so on add infinitum until we reach, via the philosophical concept of infinity, the dual philosophical concept of a true insubstantial nothingness [7] [27] .
Let us return to ![]() and in particular ponder the meaning of its continued fraction. The geometry of continued fractions is a specialized and rich subject in its own right [30] - [32] . Here we mention only on passing the geometrical relevance of continued fractions in connection with SL(2, 7) Lie symmetry groups of which the holographic boundary of E-infinity theory, i.e. SL(2, 7) is a member as well as the density points theorems on measurable subsets and multi-dimensional continued fractions [32] . However our main attention should be placed on the appearance of the remarkable prime number eleven of super gravity and Witten’s M-theory [33] - [36] . Even in the simple form given here it is obvious that
and in particular ponder the meaning of its continued fraction. The geometry of continued fractions is a specialized and rich subject in its own right [30] - [32] . Here we mention only on passing the geometrical relevance of continued fractions in connection with SL(2, 7) Lie symmetry groups of which the holographic boundary of E-infinity theory, i.e. SL(2, 7) is a member as well as the density points theorems on measurable subsets and multi-dimensional continued fractions [32] . However our main attention should be placed on the appearance of the remarkable prime number eleven of super gravity and Witten’s M-theory [33] - [36] . Even in the simple form given here it is obvious that ![]() represents a self-similar fractal-like version of the original M-theory spacetime (see [33] Figure 1 and Figure 2 as well as [36] Figure 3). It is easily reasoned that
represents a self-similar fractal-like version of the original M-theory spacetime (see [33] Figure 1 and Figure 2 as well as [36] Figure 3). It is easily reasoned that ![]() is equal to the isomorphic length of a super symmetric space [33] [36] , made of the bosonic
is equal to the isomorphic length of a super symmetric space [33] [36] , made of the bosonic ![]() and fermionic
and fermionic ![]() of E-infinity theory [19] - [21] . The intersection of both spaces gives us therefore a super symmetric space with
of E-infinity theory [19] - [21] . The intersection of both spaces gives us therefore a super symmetric space with ![]() where
where ![]() is equal to
is equal to ![]() of “tHooft-Veltman-Wilson” dimensional regularization [35] . Seen that way
of “tHooft-Veltman-Wilson” dimensional regularization [35] . Seen that way ![]() becomes not only a Hausdorff dimension but a measure for the ordinary energy density of our universe, namely [13] [16] - [25] [33] - [36]
becomes not only a Hausdorff dimension but a measure for the ordinary energy density of our universe, namely [13] [16] - [25] [33] - [36]
![]() (17)
(17)
where the 22 may be viewed as the compactified dimensional subset of the 26 dimensions of the bosonic string theory [19] - [21] . In other words, for a normed m = 1, c = 1 we have E(Einstein) = 1 and the measurable energy density is simply ![]() percent in full agreement with all actual cosmic measurements and observations [15] - [25] . Looking now at the entire situation in a global manner we could see not only that the very same mathematics which is developed for the very small is also applicable seamlessly to the extremely large but also that the physics underneath is quite similar. A band gap is evidently where a density of states function is equal zero [8] . In our spacetime model this could play the role of the empty set [33] [34] . The electrons on the other hand represent the analogue of the zero set. This is in fact quite reasonable from the viewpoint of fractal logic and the fractal counting of photons, which are the messenger particles, connected to the fermionic electron and which has a fractal weight number equal
percent in full agreement with all actual cosmic measurements and observations [15] - [25] . Looking now at the entire situation in a global manner we could see not only that the very same mathematics which is developed for the very small is also applicable seamlessly to the extremely large but also that the physics underneath is quite similar. A band gap is evidently where a density of states function is equal zero [8] . In our spacetime model this could play the role of the empty set [33] [34] . The electrons on the other hand represent the analogue of the zero set. This is in fact quite reasonable from the viewpoint of fractal logic and the fractal counting of photons, which are the messenger particles, connected to the fermionic electron and which has a fractal weight number equal ![]() rather than one. Consequently the electrons will correspond to Cantorian dust responsible for the ordinary measurable energy density [17] - [25] .
rather than one. Consequently the electrons will correspond to Cantorian dust responsible for the ordinary measurable energy density [17] - [25] .
4. Conclusions
There is one aspect of theoretical physics that is so incredibly beautiful that one cannot find the right words to describe it. This is a first hand experience of the present author which happens whenever he notices that two totally different fields can be directly connected and analogies established simply because the same stringent logic, i.e. the same mathematical pattern and schemes are obeyed by both fields. One such case is the connection between super conductivity and the high energy physics of elementary particles [1] - [4] . This is truly the unreasonable effectiveness of mathematics which on deeper still reflection, is truly reasonable.
The present work reveals a similar situation where the extremely small and large ultra obeys basically the same subgroup of R generated by Z and the golden mean number ![]() so that the density or the frequency of appearance of a motive by certain tiling, in our case Klein-Penrose fractal universe, by virtue of the basic topology must be an element of the dimensional group given by von Neumann-Connes dimensional function [11] [12] [26] [27] or equivalently the K- and E-theory bijection formula [7] [8] [12] [26] [27] . In all cases it turns out that the probability of finding a Cantorian point in the fractal M-theory space which has a Hausdorff dimension equal to 11 plus Hardy’s quantum entanglement, i.e.
so that the density or the frequency of appearance of a motive by certain tiling, in our case Klein-Penrose fractal universe, by virtue of the basic topology must be an element of the dimensional group given by von Neumann-Connes dimensional function [11] [12] [26] [27] or equivalently the K- and E-theory bijection formula [7] [8] [12] [26] [27] . In all cases it turns out that the probability of finding a Cantorian point in the fractal M-theory space which has a Hausdorff dimension equal to 11 plus Hardy’s quantum entanglement, i.e. ![]() is given simply by the inverse value of this dimension, i.e.
is given simply by the inverse value of this dimension, i.e. ![]() [33] [34] . Since such a ‘point’ is super symmetric by definition, it is a double point and
[33] [34] . Since such a ‘point’ is super symmetric by definition, it is a double point and ![]() should be divided by n = 2 to give us the net value corresponding to a single “Cantorian” [27] . We have shown here, in accordance with earlier derivations, that
should be divided by n = 2 to give us the net value corresponding to a single “Cantorian” [27] . We have shown here, in accordance with earlier derivations, that ![]() is the density of ordinary energy of the universe which accounts for only about 4.5% of the total energy while the rest, namely 1 − 4.5 = 95.5% is what has been dubbed the missing dark energy. Not only that but we established an analogous situation to a fundamental problem in condensed matter physics and showed that the very same mathematics govern the behaviour of electrons in metals as explained within the theory of gap labelling of Schrödinger operators [8] .
is the density of ordinary energy of the universe which accounts for only about 4.5% of the total energy while the rest, namely 1 − 4.5 = 95.5% is what has been dubbed the missing dark energy. Not only that but we established an analogous situation to a fundamental problem in condensed matter physics and showed that the very same mathematics govern the behaviour of electrons in metals as explained within the theory of gap labelling of Schrödinger operators [8] .
From all of the above we have considerable renewed confidence in our proposal made some two decades ago that the universe as a whole can be regarded as huge quasicrystals [37] - [43] . Clearly the proposal is indirectly implied by the work of Penrose [38] as well as a powerful but largely unsung work of a Russian school [41] . The idea was then given new impulse by the work of a leading physicist and cosmologist, P. Steinhardt [43] and it may be possible to explain the origin of the forbidden 5-D symmetry of the found meteorite remnants by the effect of the quasicrystalline geometry of quantum spacetime on its initial quantum formation [36] . In fact all recent astrophysical observations indicate a quasi self-similar universe as exposed in an excellent 2008 paper by R. Murdzek [44] , which we give here together with the superb historical account in [6] as recommended reading. We think that future research following the ideas presented here may lead to a possible harnessing of dark energy using some innovative nanotechnological devices.