1. Introduction
The projection body was introduced in 1934 by Minkowski [1] . The research on the projection body has attracted much attention. The intersection operator and the class of intersection bodies were introduced in 1988 by Lutwak [2] , who found a close connection between those bodies and famous Busemann-Petty problem (See [3] - [6] ).
In [2] , Lutwak presented the mysterious duality between projection and intersection bodies.
For convex bodies K and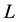 , let
, let 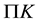 and
and 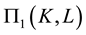 denote the projection body of K and mixed projection body of K and
denote the projection body of K and mixed projection body of K and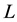 , respectively. In [7] , Lutwak established the following Brunn-Minkowski inequality for projection body and Minkowski inequality for mixed projection body:
, respectively. In [7] , Lutwak established the following Brunn-Minkowski inequality for projection body and Minkowski inequality for mixed projection body:
Theorem A. Let K and 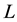 be convex bodies in
be convex bodies in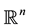 . Then
. Then
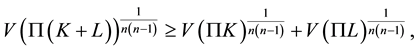 (1.1)
(1.1)
with equality if and only if K and 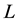 are homothetic.
are homothetic.
Theorem B. Let K and 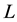 be convex bodies in
be convex bodies in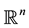 . Then
. Then
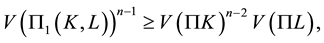 (1.2)
(1.2)
with equality if and only if K and 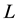 are homothetic.
are homothetic.
In [8] , Theorem A and Theorem B were extended to volume differences:
Theorem C. Suppose that K, L, and 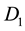 are convex bodies in
are convex bodies in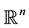 , and
, and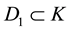 ,
, 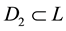 ,
, ![]() is a homo- thetic copy of
is a homo- thetic copy of![]() . Then
. Then
![]() (1.3)
(1.3)
with equality if and only if K and ![]() are homothetic and
are homothetic and![]() , where
, where ![]() is a constant.
is a constant.
Theorem D. Suppose that![]() , and
, and ![]() are convex bodies in
are convex bodies in![]() , and
, and![]() ,
, ![]() ,
, ![]() is a ho- mothetic copy of
is a ho- mothetic copy of![]() . Then
. Then
![]() (1.4)
(1.4)
with equality if and only if K and L are homothetic.
For star bodies K and![]() , let
, let ![]() and
and ![]() denote the intersection body of K and mixed intersection body of K and
denote the intersection body of K and mixed intersection body of K and![]() , respectively. In [9] , Zhao et al. established the following dual Brunn-Minkowski inequality for intersection body and dual Minkowski inequality for mixed intersection body:
, respectively. In [9] , Zhao et al. established the following dual Brunn-Minkowski inequality for intersection body and dual Minkowski inequality for mixed intersection body:
Theorem E. Let K and ![]() be star bodies in
be star bodies in![]() . Then
. Then
![]() (1.5)
(1.5)
with equality if and only if ![]() is a dilatate of K.
is a dilatate of K.
Theorem F. Let K and ![]() be star bodies in
be star bodies in![]() . Then
. Then
![]() (1.6)
(1.6)
with equality if and only if ![]() is a dilatate of K.
is a dilatate of K.
In this paper, we shall prove the dual forms of inequalities (1.3) and (1.4) for mixed intersection body. In this work new contributions that illustrate this mysterious duality will be presented. Our main results can be stated as follows:
Theorem 1.1. Let ![]() and
and ![]() are star bodies in
are star bodies in ![]() and
and![]() ,
, ![]() is a dilatation of
is a dilatation of![]() . Then
. Then
![]() (1.7)
(1.7)
with equality if and only if ![]() is a dilatate of K and
is a dilatate of K and![]() , where
, where ![]() is a constant.
is a constant.
Theorem 1.2. Let ![]() and
and ![]() are star bodies in
are star bodies in ![]() and
and![]() ,
, ![]() is a dilatation of
is a dilatation of![]() . Then
. Then
![]() (1.8)
(1.8)
with equality if and only if ![]() is a dilatate of K.
is a dilatate of K.
Please see the next section for related definitions and notations.
2. Definitions and Notations
In this section, we will recall some basic results for dual quermassintegrals of star bodies. The reader is referred to Gardner [10] , Lutwak [2] [11] and Thompson [12] for the Brunn-Minkowski theory with its dual theory.
As usual, let ![]() denote the unit ball in Euclidean
denote the unit ball in Euclidean ![]() -space,
-space,![]() . While its boundary is
. While its boundary is ![]() and its volume is denoted by
and its volume is denoted by![]() . For a compact subset K of
. For a compact subset K of![]() , with
, with![]() , star-shaped with respect to
, star-shaped with respect to![]() , the radial function
, the radial function![]() , is defined by
, is defined by
![]() (2.1)
(2.1)
If ![]() is continuous and positive, K will be called a star body.
is continuous and positive, K will be called a star body.
Two star bodies ![]() are said to be dilatate (of each other) if
are said to be dilatate (of each other) if ![]() is independent of
is independent of![]() .
.
The radial sum of two star bodies ![]() is defined as the star body K satisfying
is defined as the star body K satisfying![]() . This operation will be denoted by
. This operation will be denoted by![]() , i.e.,
, i.e., ![]()
For star bodies![]() , the dual mixed volume
, the dual mixed volume ![]() is defined by (see e.g. [11] )
is defined by (see e.g. [11] )
![]() (2.2)
(2.2)
If![]() , and
, and![]() , then the dual mixed volume
, then the dual mixed volume ![]() is called dual
is called dual ![]() -quermassintegral of
-quermassintegral of![]() , and denoted by
, and denoted by ![]() and allow
and allow![]() . It is easily seen that
. It is easily seen that![]() .
.
Let ![]() and
and ![]() be star bodies in
be star bodies in![]() . If
. If![]() , then the dual
, then the dual ![]() -quermassintegral difference function of
-quermassintegral difference function of ![]() and
and![]() ,
, ![]()
![]() , can be defined by
, can be defined by
![]() (2.3)
(2.3)
If ![]() in (2.3), then we get the volume difference of star bodies
in (2.3), then we get the volume difference of star bodies ![]() and
and![]() :
:
![]()
(See [13] for the concept of the volume difference of two compact domains).
The intersection body of a star body K, ![]() , is the centrally symmetric body whose radial function on
, is the centrally symmetric body whose radial function on ![]() is given by [2]
is given by [2]
![]() (2.4)
(2.4)
where ![]() is
is ![]() -dimensional volume.
-dimensional volume.
Let ![]() be star bodies in
be star bodies in![]() . The mixed intersection body
. The mixed intersection body ![]() of star bodies
of star bodies ![]() is defined by
is defined by
![]() (2.5)
(2.5)
where ![]() is
is ![]() -dimensional dual mixed volume.
-dimensional dual mixed volume.
If![]() ,
, ![]() , then
, then ![]() will be denoted as
will be denoted as![]() . If
. If![]() , then
, then ![]() is called the intersection body of order
is called the intersection body of order ![]() of
of![]() ; it will often be written as
; it will often be written as![]() . Specially,
. Specially,![]() . This term was introduced by Zhang [14] .
. This term was introduced by Zhang [14] .
3. Inequalities for Dual Quermassintegral Differences
In this section, we will establish two inequalities for dual quermassintegral differences of star bodies, which are generalizations of Theorem 1.1 and Theorem 1.2 presented in introduction.
Theorem 3.1. Suppose that ![]() and
and ![]() are star bodies in
are star bodies in![]() ,
, ![]() is a dilatate of
is a dilatate of![]() . If
. If![]() ,
, ![]() , then
, then
![]()
with equality if and only if ![]() is a dilatate of K and
is a dilatate of K and ![]() where
where ![]() is a constant.
is a constant.
Obviously, the case ![]() in Theorem 3.1 is just Theorem 1.1. Furthermore, taking
in Theorem 3.1 is just Theorem 1.1. Furthermore, taking ![]() and
and ![]() to be two closed balls with radii
to be two closed balls with radii ![]() and
and ![]() in Theorem 1.1, we infer
in Theorem 1.1, we infer
Corollary 3.2. Let ![]() and
and ![]() be the circumradii of star bodies K and L. If
be the circumradii of star bodies K and L. If![]() ,
, ![]() , then
, then
![]()
with equality if and only if ![]() is a dilatate of K and
is a dilatate of K and![]() .
.
Theorem 3.3. Suppose that ![]() and D1 are star bodies in
and D1 are star bodies in![]() , D2 is a dilatate of D1. If
, D2 is a dilatate of D1. If![]() , and
, and![]() . Then
. Then
![]()
with equality if and only if ![]() is a dilatate of K and
is a dilatate of K and ![]() where
where ![]() is a constant.
is a constant.
Obviously, the case ![]() in Theorem 3.3 is just Theorem 1.2.
in Theorem 3.3 is just Theorem 1.2.
We will require some additional notations and two analytic inequalities to prove Theorem 3.1 and Theorem 3.3. Firstly, we define a function ![]() by
by
![]()
where ![]() for p > 0. Note that
for p > 0. Note that ![]() is an indefinite form of its variables.
is an indefinite form of its variables.
Lemma 3.4. If![]() ,
, ![]() , then
, then![]() , and
, and
![]() (3.1)
(3.1)
with equality holds if and only if the coordinates of ![]() are proportional.
are proportional.
A proof of Lemma 3.4 can be found in [15] . The inequality (3.1) was first proved by Bellman [16] and is known as Bellman’s inequality.
Lemma 3.5. If![]() ,
, ![]() and
and![]() . Let
. Let ![]() and
and![]() , then
, then
![]()
with equality if and only if![]() .
.
Proof. Consider the following function
![]()
Let
![]()
We get![]() .
.
On the other hand, if![]() , then
, then![]() ; if
; if ![]() then
then![]() , and it follows that
, and it follows that
![]()
This completes the proof.
Lemma 3.6. [15] Let ![]() be star bodies in
be star bodies in![]() . If
. If![]() , then
, then
![]() (3.2)
(3.2)
and
![]() (3.3)
(3.3)
with equality if and only if ![]() is a dilatate of
is a dilatate of![]() .
.
Proof of Theorem 3.1. For star bodies![]() , applying inequality (3.2), we have
, applying inequality (3.2), we have
![]() (3.4)
(3.4)
with equality if and only if ![]() is a dilatate of
is a dilatate of![]() .
.
![]() (3.5)
(3.5)
Since![]() , we get
, we get
![]()
From (3.4) and (3.5), we obtain that
![]()
Then by Lemma 3.4, we get
![]() (3.6)
(3.6)
Note that the equality holds in (3.4) if and only if L is a dilatate of K. By Lemma 3.4 we know that the equality holds in (3.6) if and only if L is a dilatate of K. and ![]() is proportional to
is proportional to ![]()
This completes the proof.
Proof of Theorem 3.3. Applying inequality (3.3), we have
![]()
with equality if and only if ![]() is a dilatate of
is a dilatate of![]() .
.
![]()
Hence, by Lemma 3.5, we obtain that
![]()
The proof is complete.
Acknowledgments
We thank the Editor and the referee for their comments. The research is supported by National Natural Science Foundation of China (11101216), Qing Lan Project and the Nanjing Xiaozhuang University (2010KYQN24, 2010KYYB13).
NOTES
*Corresponding author.