On the FOM Algorithm for the Resolution of the Linear Systems Ax = b ()
1. Introduction
The resolution of linear systems 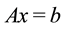 is in the heart of numerous scientific applications: discretization of partiel differentiel equations, image processing, the linearization of nonlinear problems in a sequence of linear problems [1] [2] [3] etc. There are many kinds of methods that resolve linear systems. Some are direct, others are iterative. Generally, direct methods [4] - [6] , such as Gauss, Cholesky, QR, are efficient and proved solvers of small size systems. But for problems of big size, these methods require quite prohibitive memory space and therefore become numerically expensive. More and more, they are replaced by iterative methods. Most iterative methods [2] [6] [7] treat linear systems through vector-matrix products with an appropriate data structure permitting the exploitation of sparsity of the matrix
is in the heart of numerous scientific applications: discretization of partiel differentiel equations, image processing, the linearization of nonlinear problems in a sequence of linear problems [1] [2] [3] etc. There are many kinds of methods that resolve linear systems. Some are direct, others are iterative. Generally, direct methods [4] - [6] , such as Gauss, Cholesky, QR, are efficient and proved solvers of small size systems. But for problems of big size, these methods require quite prohibitive memory space and therefore become numerically expensive. More and more, they are replaced by iterative methods. Most iterative methods [2] [6] [7] treat linear systems through vector-matrix products with an appropriate data structure permitting the exploitation of sparsity of the matrix 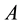 by storing only nonzero elements which are indi- spensable for the calculation of these products, which reduces both the memory size and the processing time. We distinguish two kinds of iterative methods for the resolution of linear systems:
by storing only nonzero elements which are indi- spensable for the calculation of these products, which reduces both the memory size and the processing time. We distinguish two kinds of iterative methods for the resolution of linear systems:
 The asymptotic methods [6] - [8] are older and simpler to implement. Among the most known ones, we mention
Jacobi
’s, Gauss-Seidel’s and the relaxation methods. Generally, these methods remain less reliable than the direct methods, and more or less efficient with some specific problems. Currently, these methods are no longer used as linear solvers but remain interesting as preconditioners for other iterative methods. The increase of the size of the systems to be solved leads to the projection methods.
The asymptotic methods [6] - [8] are older and simpler to implement. Among the most known ones, we mention
Jacobi
’s, Gauss-Seidel’s and the relaxation methods. Generally, these methods remain less reliable than the direct methods, and more or less efficient with some specific problems. Currently, these methods are no longer used as linear solvers but remain interesting as preconditioners for other iterative methods. The increase of the size of the systems to be solved leads to the projection methods.
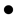 Krylov methods: They are being used for some time and proved to be very efficient [2] . Their analysis is more complicated than that of the asymptotic methods. They are based on a technique of projection on a Krylov
Krylov methods: They are being used for some time and proved to be very efficient [2] . Their analysis is more complicated than that of the asymptotic methods. They are based on a technique of projection on a Krylov
subspace, having the form: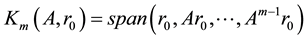 ;
;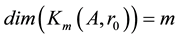 , spanned by the succe-
, spanned by the succe-
ssive powers of  applied to the risudual vector
applied to the risudual vector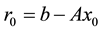 , where
, where 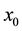 is a vector of
is a vector of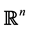 , these Krylov’s subspaces constitute an increasing sequence of subspaces, one being included in the other and permitting the construction of a sequence of vectors converging towards the solution. The convergence of these methods is theorically assured for
, these Krylov’s subspaces constitute an increasing sequence of subspaces, one being included in the other and permitting the construction of a sequence of vectors converging towards the solution. The convergence of these methods is theorically assured for  maximum. The Krylov methods resolve linear systems having nonsymmetric matrices. The most used Krylov methods based on Arnoldi algorithm are: the full orthogonalization method (FOM) and its varieties: the method of minimal residue (or shortly GMRES), Lanczos method, and that of conjugate gradient for symmetric and symmetric positive definite matrices. These projection methods are more generalisable, more powerful and currently the most used.
maximum. The Krylov methods resolve linear systems having nonsymmetric matrices. The most used Krylov methods based on Arnoldi algorithm are: the full orthogonalization method (FOM) and its varieties: the method of minimal residue (or shortly GMRES), Lanczos method, and that of conjugate gradient for symmetric and symmetric positive definite matrices. These projection methods are more generalisable, more powerful and currently the most used.
In the first section, we will review the orthogonal projection methods on Krylov’s subspaces, focusing on the FOM method for the resolution of linear systems.
In the second section, we will extend the definition of Sturm sequence, which will serve for the calculation of the determinant of upper hessenberg matrices.
In the third section, we will give a new variety of Givens method [4] for the resolution of linear systems having an upper hessenberg matrix.
Finally, in the fourth section, we report the results of some numerical tests.
In what follows, we consider a real regular square matrix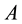 , a vector
, a vector  and the correspondent linear system:
and the correspondent linear system:
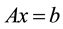 (1)
(1)
If 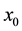 is a starting approximation of solution (1), then the residual vector associated to
is a starting approximation of solution (1), then the residual vector associated to ![]() is
is![]() . We call Krylov space of order
. We call Krylov space of order![]() , noted
, noted![]() , the vectorial space spanned by
, the vectorial space spanned by ![]() and its
and its ![]() iterated by
iterated by![]() :
:
![]() (2)
(2)
1.1. The Projection Method
In this part, we will review generallities over iterative methods of projection for the resolution of linear systems (1), by using projections in particular subspaces, namely Krylov’s spaces [1] [2] .
Most actual iterative techniques used in solving large linear systems use in one way or another a projection procedure. The main idea of projection techniques consist in extracting an approximate solution to system (1) of a subspace of![]() . It leads to a small linear system. This is a basic projection step. If we take
. It leads to a small linear system. This is a basic projection step. If we take ![]() of
of ![]() dimension (the subspace searched for), then, generally,
dimension (the subspace searched for), then, generally, ![]() constraints must be imposed in order to be able to extract such an approximation. One usual way of describing these constraints is to impose to the residual vectors
constraints must be imposed in order to be able to extract such an approximation. One usual way of describing these constraints is to impose to the residual vectors ![]() to be orthogonal to the linearly independent
to be orthogonal to the linearly independent ![]() vectors, this will define another subspace noted
vectors, this will define another subspace noted ![]() with dimension
with dimension![]() , which we call “constraints space”. We are then seeking an approximate solution
, which we call “constraints space”. We are then seeking an approximate solution ![]() to problem (1) by imposing that
to problem (1) by imposing that ![]() and that the new residual vector
and that the new residual vector ![]() must be orthogonal to
must be orthogonal to![]() . If, in addition, we want to use the starting approximation
. If, in addition, we want to use the starting approximation![]() , then the approximate solution
, then the approximate solution ![]() must be searched for in the affine space
must be searched for in the affine space![]() , then the solution of (1) will be characterized as follows:
, then the solution of (1) will be characterized as follows:
![]() (3)
(3)
As such, the definition of the projection method is based on two conditions:
![]() The first fixes the “place” where we should look for the solution at the
The first fixes the “place” where we should look for the solution at the ![]() iteration: usually, this place is an affine subvariety of
iteration: usually, this place is an affine subvariety of![]() . According to Krylov’s methods, this affine subvariety is
. According to Krylov’s methods, this affine subvariety is![]() , which gives us the following “space condition”:
, which gives us the following “space condition”:
![]() (4)
(4)
![]() The second condition must fix the
The second condition must fix the ![]() that is appropriate to that space (4). We hope that
that is appropriate to that space (4). We hope that ![]() minimizes the vector error
minimizes the vector error![]() , or the residual vector
, or the residual vector ![]() or one or those two vectors be orthogonal to a space
or one or those two vectors be orthogonal to a space ![]() of dimension
of dimension![]() . This condition is called “Petrov-Galerkin condition”, and is expressed as follows:
. This condition is called “Petrov-Galerkin condition”, and is expressed as follows:
![]() (5)
(5)
As for the projection method, we will study in the next part, Arnoldi’s method for the resolution of linear systems. Let’s start now by recalling Arnoldi’s algorithm.
1.2. Arnoldi’s Algorithm
Arnoldi’s Algorithm is an iterative process consisting in calculating, simultaneously, an orthonormal basis ![]() of
of![]() , and an upper hessenberg matrix
, and an upper hessenberg matrix![]() . The matrix
. The matrix ![]() is a representation of
is a representation of ![]() with respect to this basis.
with respect to this basis.
In practice, constructing Krylov’s spaces leads to determining basis. The natural basis ![]()
can never be used, due to its numerical degeneration, and the Krylov’s matrices become increasingly ill-condi- tioned [2] . To avoid this numerical degeneration of the natural basis of Krylov’s space, the solution consists in putting in place an orthonormalization process. Arnoldi’s basis is then constructed by applying the modified Gram-Schmidt orthonormalization method to vectors obtained by successive products matrix vector for euclidien inner product. The Arnoldi’s algorithm takes the following form:
![]()
If we assign ![]() as coefficient of orthogonalization of
as coefficient of orthogonalization of ![]() with respect to
with respect to![]() ,
, ![]() and
and ![]() as norm of vector
as norm of vector ![]() obtained by orthogonalization of vector
obtained by orthogonalization of vector ![]() with respect to vectors
with respect to vectors![]() , then, the formula of Arnoldi’s basis construction can be written:
, then, the formula of Arnoldi’s basis construction can be written:
![]() (6)
(6)
Let ![]() be the matrix having
be the matrix having ![]() rows and
rows and ![]() columns, in which the
columns, in which the ![]() columns are the first vectors of the Arnoldi’s basis. The orthonormality of vectors, in terms of matrices can be written:
columns are the first vectors of the Arnoldi’s basis. The orthonormality of vectors, in terms of matrices can be written:
![]() (7)
(7)
Likewise, Equation (6), which defines Arnoldi’s vectors, can be translated matricially by:
![]() (8)
(8)
where the matrix ![]() is a matrix having
is a matrix having ![]() rows and
rows and ![]() columns where
columns where ![]() coefficients are the coefficients of orthonormalization of the Equation (6): where
coefficients are the coefficients of orthonormalization of the Equation (6): where ![]() for
for![]() , and the other coefficients being zero.
, and the other coefficients being zero.
![]() (9)
(9)
The main diagonal block of ![]() is a square matrix of dimension
is a square matrix of dimension![]() , noted
, noted![]() , which, according the Equations (7) and (8), verifies:
, which, according the Equations (7) and (8), verifies:
![]() (10)
(10)
Such a matrix is called “upper hessenberg”:![]() .
.
Equation (10) shows that ![]() is the matrix of the projection in Krylov’s space
is the matrix of the projection in Krylov’s space ![]() of the linear map associated to the matrix A, in the basis
of the linear map associated to the matrix A, in the basis ![]() of Arnoldi’s vectors. This can be summed up as follows:
of Arnoldi’s vectors. This can be summed up as follows:
Proposition 1:
In Arnoldi’s algorithm![]() , we have at the step
, we have at the step ![]() the following relations:
the following relations:
![]() (11)
(11)
where ![]() is the vector of the canonical basis of
is the vector of the canonical basis of ![]()
Proof: [2] .
1.3. Arnoldi’s Method for Linear Systems (FOM)
In this paragraph, we will remind the important results needed for the resolution of linear systems (1).
For that, we will begin by applying the Arnoldi’s algorithm ![]() to the matrix
to the matrix![]() , this allows us to obtain at each step
, this allows us to obtain at each step![]() , a matricial pair
, a matricial pair ![]() where
where ![]() is an orthonormal basis of Krylov’s space
is an orthonormal basis of Krylov’s space![]() , and
, and
![]() is specific an upper hessenberg matrix given by (9).
is specific an upper hessenberg matrix given by (9).
The full orthogonalization method (FOM) is variant of problem (3), verifying the space condition (4) and “Petrov-Galerkin condition” (5) by taking![]() . This method is defined by:
. This method is defined by:
![]() (12)
(12)
Production of the Solution
We are seeking the solution ![]() verifying the space condition (4) and “Petrov-Galerkin condition” (5).
verifying the space condition (4) and “Petrov-Galerkin condition” (5).
(4) ![]() with
with![]() .
.
So, the residual vector ![]() is written:
is written:
![]() (13)
(13)
and “Petrov-Galerkin condition” becomes:
(5)![]()
![]() , with (13)
, with (13)
![]() but then
but then
![]() . This is equivalent to:
. This is equivalent to:
![]() (14)
(14)
So, (14) implies![]() , and the solution
, and the solution ![]() can be written:
can be written:
![]() (15)
(15)
and the problem becomes:
![]()
A method based on this approach is called a full orthogonalization method (FOM). It is given by
Y.
Saad
in 1981.
This is the corresponding algorithm using the Arnoldi’s process![]() .
.
![]()
The algorithm ![]() depends on parameter
depends on parameter![]() , which is the dimension of the Krylov’s subspace. In practice, it is desirable to select
, which is the dimension of the Krylov’s subspace. In practice, it is desirable to select ![]() in a dynamic way. This is possible if the norm of the residue
in a dynamic way. This is possible if the norm of the residue ![]() of the solution
of the solution ![]() is calculated with a numerically low cost. (without having to compute
is calculated with a numerically low cost. (without having to compute ![]() itself). Then the algorithm can be stopped at the appropriate step using this information. The following result gives an answer in this direction.
itself). Then the algorithm can be stopped at the appropriate step using this information. The following result gives an answer in this direction.
Proposition 2:
The residue vector ![]() of the approximate solution
of the approximate solution ![]() calculated by the algorithm
calculated by the algorithm ![]() is such that:
is such that:
![]()
and so,
![]() (16)
(16)
Proof: [2] .
At this stage, the interesting feature is the possibility to compute the norm of residue without producing the solution.
According to this proposition, at the step![]() , the residual norm
, the residual norm ![]() is then given directly by the absolute value of the last component
is then given directly by the absolute value of the last component ![]() of the vector
of the vector![]() . This provides the stopping test and
. This provides the stopping test and
allows to calculate ![]() only when the stopping criterion used for the solution is satisfied. This is the main idea of this article. It consists in calculating locally, at each iteration
only when the stopping criterion used for the solution is satisfied. This is the main idea of this article. It consists in calculating locally, at each iteration![]() , uniquely the last component
, uniquely the last component ![]() of the
of the
vector![]() : solution of the system (14)
: solution of the system (14)![]() . The classical formulae of Cramer’s rule directly gives the component
. The classical formulae of Cramer’s rule directly gives the component ![]() in the form of a determinant quotient:
in the form of a determinant quotient:![]() , the computation of determi-
, the computation of determi-
nants ![]() is given by the following result:
is given by the following result:
Proposition 3:
Let ![]() be an invertible upper hessenberg matrix and
be an invertible upper hessenberg matrix and![]() , the second member of the linear system (14)
, the second member of the linear system (14)![]() . Then we have:
. Then we have:
![]() (17)
(17)
with:
![]() (18)
(18)
![]() (19)
(19)
What we need now, is to calculate![]() ;
; ![]() being an upper hessenberg matrix.
being an upper hessenberg matrix.
2. Sturm Sequence for the Upper Hessenberg Matrices (U.H)
In this paragraph, we extend the definition of Sturm sequence to the hessenberg matrices, and then we give an algorithm computing their determinants. Let’s start by reminding the following principal result:
Proposition 4:
Let ![]() be an (U.H) matrix and let
be an (U.H) matrix and let ![]() be the
be the ![]() principal submatrix of
principal submatrix of![]() , i.e.,
, i.e.,
![]()
and let ![]() be the charcteristic polynomial of
be the charcteristic polynomial of![]() , then: the polynomial
, then: the polynomial![]() ,
, ![]() are given by to the following recurrent formula :
are given by to the following recurrent formula :
![]() (20)
(20)
Proof: by recurrence.
Definition 1:
The sequence ![]() defined by (20) is called Sturm sequence of the upper hessenberg matrix.
defined by (20) is called Sturm sequence of the upper hessenberg matrix.
Remark 1:
We note that, for the programming, we can win ![]() memory words if we use a storage numbering
memory words if we use a storage numbering
function [8] for upper hessenberg matrices by storing nonzero elements uniquely.
2.1. Computing the Determinant of the Hessenberg Matrix ![]()
For calculating the determinant of an upper hessenberg matrix, Proposition (2) gives us a simple method in![]() . This can be summed by the following result:
. This can be summed by the following result:
Corollary 1:
Let ![]() be an invertible (U.H) matrix. If we set
be an invertible (U.H) matrix. If we set![]() , then we have:
, then we have:
![]() (21)
(21)
![]() . In the Formula (21), we calculate the products
. In the Formula (21), we calculate the products![]() , without repeting multiplications. So, we obtain a very interesting algorithm
, without repeting multiplications. So, we obtain a very interesting algorithm ![]() computing
computing ![]() as follows:
as follows:
![]()
The number of operations necessary in calculating ![]() is:
is:
![]() additions:
additions: ![]()
![]() multiplications:
multiplications:![]() .
.
The total number of operations required is![]() . This is more convenient when
. This is more convenient when ![]() is big.
is big.
We will adopt the algorithm ![]() in the full orthogonalization method (FOM). Having at each step
in the full orthogonalization method (FOM). Having at each step![]() ,
,
![]() , we calculate by the Formulaes (18) and (19):
, we calculate by the Formulaes (18) and (19):![]() . This gives us the stopping test and
. This gives us the stopping test and
allows to calculate ![]() only when the stopping criterion used for the solution is satisffied, namely:
only when the stopping criterion used for the solution is satisffied, namely:
![]()
where![]() , being the required precision. The FOM algorithm
, being the required precision. The FOM algorithm ![]() takes the following form:
takes the following form:
![]()
When the stopping criterion used for the solution is satisffied, we take the value ![]() for calculating
for calculating ![]()
![]() by using the following algorithm:
by using the following algorithm:
2.2. Algorithm of Resolution of the System: ![]()
![]()
The above algorithm ![]() requires
requires ![]() flops.
flops.
Several authors solve the linear system ![]() using Givens method applied to an upper hessenberg matrix.
using Givens method applied to an upper hessenberg matrix.
3. The Givens Method for (U.H) Matrices
In this section, we give a new variant of the Givens method for the resolution of linear systems with an upper hessenberg matrices coming from Arnoldi’s algorithm. This method is based on the addition of two matrices and two tensorial products.
The Givens rotations constitute an important tool to selectively eliminate certain coefficients of a matrix. This is the case of our upper hessenberg matrix, where we eliminate the codiagonal in order to obtain an upper triangular matrix.
To justify the next results, we introduce the following notations:
![]()
![]() : the
: the ![]() row of the matrix
row of the matrix ![]() at the step
at the step![]() .
.
![]()
![]() : the matrix
: the matrix ![]() with the
with the ![]() and
and ![]() row put to zero.
row put to zero.
![]()
![]() :
: ![]() column vector of
column vector of![]() .
.
![]()
![]() : the superscript
: the superscript ![]() will denote the matrix or the transposed vector.
will denote the matrix or the transposed vector.
![]()
![]() : tensor product of two vectors
: tensor product of two vectors ![]() in
in![]() .
.
![]()
![]() :
: ![]() column vector of the rotation matrix
column vector of the rotation matrix ![]() in the plan
in the plan![]() .
.
3.1. Givens Formulation for Upper Hessenberg Matrices
The classical formulation of the Givens method for an upper hessenberg matrix ![]() is given under the following form:
is given under the following form:
![]() (22)
(22)
with ![]() is of the form:
is of the form:
![]() (23)
(23)
with ![]() and where
and where ![]() and
and ![]() are calculated at each step
are calculated at each step ![]() by the following formulas:
by the following formulas:
![]() (24)
(24)
The relations (22) give us an upper triangular matrix,![]() :
:
![]() (25)
(25)
and therefore ![]()
As the matrices ![]() are orthogonal, we have:
are orthogonal, we have:![]() , from which
, from which
![]() (26)
(26)
Theorem 1:
If ![]() is an invertible upper hessenberg matrix, then
is an invertible upper hessenberg matrix, then ![]()
![]() (27)
(27)
where ![]() is the
is the ![]() row vector of the matrx
row vector of the matrx ![]() and
and ![]() is the
is the ![]() column vector of the matrix
column vector of the matrix![]() .
.
The Givens algorithm for the triangularisation of the matrix ![]() (U.H), is simplified to be written in its new form:
(U.H), is simplified to be written in its new form:
![]()
3.1.1
. Complexity of the Algorithm ![]()
To eliminate the (n − 1) elements situated under the diagonal, we need (n − 1) rotations![]() . Each rotation requires 5 operations and an extraction of a square root
. Each rotation requires 5 operations and an extraction of a square root![]() .
.
For a fixed k
® Computation of tensor product:
![]() :
:
![]() :
:
® Computation of matricial addition:
![]() :
:
and![]() , we have:
, we have:
![]()
Conclusion: The complexity of Givens’ algorithm ![]() for an upper hessenberg matrix requires
for an upper hessenberg matrix requires ![]() flops and
flops and![]() .
.
In consequense, we find the calculating formula of the determinant of the matrix ![]() given by:
given by:
Corollary 2 :
Let ![]() be an (U.H) matrix. By applying classical Givens’ formulation, given by the relation (22) and the Formula (26), we obtain:
be an (U.H) matrix. By applying classical Givens’ formulation, given by the relation (22) and the Formula (26), we obtain:
![]() (28)
(28)
We can decompose ![]() matrix (U.H) of rank
matrix (U.H) of rank![]() , into an addition of a triangular matrix and
, into an addition of a triangular matrix and ![]() matrices of rang 1 given by:
matrices of rang 1 given by:
![]() (29)
(29)
3.1.2
. Numerical Example
Let ![]() be an invertible matrix (U.H), and
be an invertible matrix (U.H), and![]() .
.
We want to resolve![]() .
.
![]()
We apply the algorithm ![]() to the augmented matrix
to the augmented matrix ![]() by the second member
by the second member![]() .
.
step k = 1
![]() Compute the rotation in plane
Compute the rotation in plane![]() :
: ![]()
Column 1:![]() ; column 2:
; column 2: ![]()
![]()
step k = 2
![]() Compute the rotation in plane
Compute the rotation in plane![]() :
: ![]()
Column 2:![]() ; column 3:
; column 3: ![]()
![]()
step k = 3
![]() Compute the rotation in plane
Compute the rotation in plane![]() :
: ![]()
Column 3:![]() ; column 4:
; column 4: ![]()
![]()
we obtain a triangular system ![]() whose solution is
whose solution is![]() :
:
![]()
and we have![]() .
.
4. Numerical Tests
In this section, we present four numerical tests for the resolution of linear systems (1): ![]() for the pro- posed new version of full orthogonalization method (FOM). These tests are done using a portable DELL (Latitude D505 intel (R) Pentium (R) M, processor 1.70 GHz, 594 MHz) and a program written in
for the pro- posed new version of full orthogonalization method (FOM). These tests are done using a portable DELL (Latitude D505 intel (R) Pentium (R) M, processor 1.70 GHz, 594 MHz) and a program written in![]() , with double precision.
, with double precision.
Test 1: ![]() is band (SPD) matrix
is band (SPD) matrix![]() ,
, ![]() , [9] and
, [9] and ![]() is the exact solution.
is the exact solution.
![]()
From test 1, we deduce the following numerical results in Table 1.
Test 2: ![]() is a full matrix,
is a full matrix, ![]() is the exact solution, and
is the exact solution, and ![]() is the inverse matrix.
is the inverse matrix.
![]()
where: ![]() which imply:
which imply:![]() .
.
![]() (30)
(30)
From test 2, we deduce the following numerical results in Table 2.
Test 3:
In the third test, we focus our attention on the resolution of the partial differential equations with Neuman condition:
![]() (31)
(31)
with: ![]()
![]()
Table 1. Test
1’
s numerical results.
![]()
Table 2. Test
2’
s numerical results.
If we consider ![]() as a solution, we obtain the function:
as a solution, we obtain the function:
![]() (32)
(32)
as a second member.
After doing a regular maillage and numbering the nodes, the calculation of the stiffness matrix leads to a (SPD) “well-conditioned” matrix. For the resolution we use the new version of full orthogonalization method (FOM).
Table 3 contains the numerical results of Test 3:
Test 4: ![]() is band, (SPD) matrix
is band, (SPD) matrix![]() ,
, ![]() , [9] .
, [9] .
![]()
![]() (33)
(33)
On the one hand, the numerical results for the matrices ![]() are considerably polluted with rounding errors because the matrices
are considerably polluted with rounding errors because the matrices ![]() are very “ill-conditioned” But on the other hand, we are constructing matrices
are very “ill-conditioned” But on the other hand, we are constructing matrices ![]() very “well-conditioned” from matrices
very “well-conditioned” from matrices ![]() with translations:
with translations:
![]()
where![]() .
.
From Test 4, we deduce the following numerical results in Table 4.
![]()
Table 3. Test
3’
s numerical results.
![]()
Table 4. Test
4’
s numerical results.
5. Conclusions
Test 1 and 2 show the results of applying the proposed new version of full orthogonalization method (FOM): the dimension ![]() of Krylov’s space
of Krylov’s space ![]() is acceptable compared to
is acceptable compared to ![]() because the matrices
because the matrices ![]() are moderately “ill-conditioned”.
are moderately “ill-conditioned”.
For the third test, the stiffness matrix coming from the discretization of the partial differential Equations (31) leads to a (SPD) well-conditioned matrix. We note that dimension ![]() of Krylov’s space
of Krylov’s space ![]() is weak com- pared to
is weak com- pared to![]() , which can give a positive judgment about the new version of (FOM) method.
, which can give a positive judgment about the new version of (FOM) method.
In the final test, the constructed matrices ![]() are very “well-conditioned”, and the dimension
are very “well-conditioned”, and the dimension ![]() is as small as required.
is as small as required.
Acknowledgements
The author is grateful to the referees for their valuable comments and suggestions which have helped to improve the presentation of this work.