Predispatch of Hydroelectric Power Systems with Modifications in Network Topologies ()
1. Introduction
In an electric power system, operating conditions are constantly evolving; accordingly, maintenance services must be performed to avoid short-circuits and overloads. Scheduled shutdowns are recommended when system maintenance is necessary. Therefore, the goal is to ensure the supply of electrical energy with few interruptions for the shortest time possible while maintaining the quality levels established in legislation governing the electricity sector.
The occurrence of scheduled or emergency interruptions in a power transmission network requires the isolation and restoration manipulations on the network. The operations that define a manipulation must comply with previously-established electrical requirements and criteria, regulated by government agencies or by the power distribution utility.
Considering the complexity of electrical power grids, the increased demand for energy and the constant quest for lower costs, the application of methods to minimize generation costs and losses in the predispatch transmission of the system has become necessary.
In hydroelectric predispatch, power plants have a goal to accomplish on a given day, which is established by long-term planning. On the other hand, with the variation in demand due to the time period, the execution of programmed manipulations on the transmission lines or generation buses is necessary to keep the system stable, thus leading to changes in the configuration of the network throughout the day.
In this study, the predispatch is modeled over a twenty-four-hour period, representing the dispatch in a single day, and the manipulations will be a data input, i.e., they will already be programmed; therefore the manipulations considered herein will be preventive. It is important to highlight that there are other types of manipulations, such as generator shutdowns, tap changing and FACTS (Flexible Alternating Current Transmission System) adjustment; however, these will not be considered in this study.
In this paper, the predispatch model for a system hydroelectric is initially approached where manipulations are not considered. A solution to this problem using primal-dual interior point method is presented. Then the problem with manipulations is inserted, explaining the differences between bar manipulation and line manipulation, as well as incidence and reactance matrices changes according with the new network topology. A heuristic for the construction of a spanning tree is discussed, since it is necessary depending on the manipulation to be performed. This paper finalizes with computational results in test and real life systems and the conclusions.
Furthermore, by using the speed and robustness of the interior-point methods [1] -[3] , the goal is to obtain more efficient implementations for the predispatch through the exploitation of the matrix structure of the resulting system.
2. The Predispatch Problem
Predispatch is a short-term operational problem; in this case, short-term refers to one week, or even one day, The intention is to fulfill demands and satisfy the energy targets that have been defined in long-term planning. Flow restrictions can be divided into blocks that repeat themselves over a certain time interval, representing the power system in these intervals. We also have an independent formulation of the Kirchhoff laws, where power flows are represented by directly considering transmission limits as restrictions and transmission losses as performance criteria [4] .
DC network power flow models are in widespread and even increasing use, particularly in congestion-constrained market applications, since they have considerable analytical and computational appeal. When their power flows are reasonably correct, they can often offer compelling advantages [5] .
A predispatch system with 
buses, 
lines and 
generators, where manipulations are not considered, can be modeled as follows [6] :
(1.1)
where:
• 
represents the active power flow variables;
• 
represents the active power generation variables;
• 
represents the diagonal matrix of the generation loss quadratic term;
• 
represents the diagonal resistance matrix;
• 
represents the active load demand;
• 
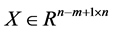represents the network loop reactance matrix;
• 
represents the matriz of dimension 
with each column containing a single nonzero entry equals to one for each generator;
• 
represents the network incidence matrix;
• 
represents the linear term of generation loss coefficient vector;
• 
and 
are bounds for the active power flow and generation variables;
• 
are weight constants;
• 
represents the generating unit targets.
In this model, the two objective function components are quadratic with separable variables. The first component represents the value of the transmission losses. The second component characterizes the generation cost of power plants [7] .
Problem (1.1) may be simplified by using changes in the variables [8] and adding slack variables, thus we have the primal problem in its standard form:
(1.2)
whose respective dual can be written as:
(1.3)
Matrix
, formed by the juxtaposed rows of the incidence and reactance matrix, is no longer constant throughout the time intervals
, which may be partitioned as:
In more detail:
where,
and,
.
with this partitioning, the columns of the incidence matrix A are divided so that T contains the edges of a spanning tree and N is formed by the remaining edges, which belong to the co-tree [9] , and the reactance matrix 
in a similar manner. Matrices 
and 
vary according to the time intervals (
and
), reflecting the modifications to the networks and buses by the manipulations carried out throughout the study window. The reason why these matrices vary according to time intervals is that the network is no longer constant throughout these t intervals; every time there is a manipulation, the matrix 
formed by the juxtaposed rows of the incidence and reactance matrix and the matrix 
of order 
should vary in accordance with the changes imposed on the network.
The primal-dual interior-point methods consist of the application of Newton’s method to the optimality conditions; therefore, the following linear system is obtained:
(1.4)
when several variable substitutions are made, we get:
(1.5)
By eliminating the 
from the first equation of the previous system and replacing it in the second equation, we get:
(1.6)
The direct solution of the linear system (1.6) requires a large computational effort because the blocks
have the dimension of transmission lines and the dya dimension is given by the of number of generators. A more efficient solution, inspired by [6] , will be developed for the model with topology network modification.
3. Manipulations
The manipulations may occur due to momentary unscheduled interruptions, or to meet the needs of network maintenance and transfers of loads, feeders and substations. In Brazil, the System Operation Center (COS) is responsible for executing, authorizing and overseeing the manipulations and scheduled or emergency services of the electricity transmission system. It monitors and effectively operates in restoring the electricity system in the event of simple and generalized contingencies. Such activities, carried out in real time, cover the knowledge of the situation and orientation on the execution of any manipulations that may be required, aimed at ensuring the integrity of people and facilities, system reliability and reliability and quality of supply.
Over most time intervals, manipulations are not executed in the Brazilian electricity system, rarely causing the transmission network to change from one interval to another, with four to six manipulations typically being executed per day. The changes considered herein will be called preventive manipulations, i.e., those changes that occur on the network so that maintenance can be carried out, thus avoiding power interruption.
The goal is to meet all the loads, without straining lines, feeders and power generation plants.
Three types of manipulations will be considered in this study:
• line manipulations;
• bus manipulations.
3.1. Line Manipulations
Line manipulations represent the shutdown or return to operation of certain transmission lines. When a line manipulation is executed, for instance, a branch is removed from the system, the network topology is modified. Algebraically, a column from the incidence matrix, concerning the branch manipulated, and a row from the reactance matrix are removed [10] .
3.2. Predispatch Model with Line Manipulation
The predispatch problem complies with a model involving repetitions in t time intervals, which characterize the study window. The predispatch problem with manipulations can be formulated in the standard form as:
(1.7)
This problem is similar to the case without manipulations (1.1). However, matrices 
and 
vary according to time intervals (
and
), reflecting the modifications to the networks and buses by the manipulations executed throughout the study window.
The following sections detail the aspects exploited, taking into account the different types of manipulations.
3.3. Study of Matrix Structure for the Problem with Line Manipulations
We presuppose that the preprogrammed manipulations 
occur along the time intervals
, where each time interval corresponds to a period of 1 or 1/2 hour.
Matrix
, formed by the juxtaposed rows of the incidence and reactance matrix, is no longer constant throughout the time intervals
. Each time a manipulation is executed, a row and a column from matrix 
are removed (inserted). In case there is more than one manipulation in the same time interval, a larger number of rows and columns from matrix B are removed (inserted).
When we consider a system with manipulations at different time intervals, we will use the following notation:
where,
.
As the dimension of matrix B can be modified at every manipulation, the system must be adjusted to these alterations; that is, for the execution of the product and summation with B, the dimensions and structures of the other matrices involved in the system (arising from the characteristics of B) are modified.
As we have already said, matrix 
can be decomposed as:
where
and
with this partitioning, the columns of the incidence matrix 
are divided so that T contains the edges of a spanning tree and N is formed by the remaining edges, which belong to the co-tree [9] . The reactance matrix X is partitioned in a similar manner.
In Figure 1, we have the nodes and edges of an electric system, where the rows in bold represent a spanning tree and the other lines are its additional edges.
Figure 2 is an electric system graph, where the dotted lines represent the branches of the system to be disconnected, whose incidence matrix is shown in Figure 3.
3.4. Solving the Predispatch Problem with Line Manipulations
Next we will study the consequences of the line manipulations in the matrix structure. We have observed that, in Equation (1.5), which does not consider manipulations, the matrix
(1.8)
is square and has the dimension
, where its first 
lines constitute the diagonal matrix
, while the remainder of its elements are null.
We can observe that the matrices that are directly influenced by the change in dimension of 
are
, 
and
. Thus, when performing the manipulations in the system, Equation (1.8) will be the following:
.
Figure 1. Spanninh tree edges in bold and additional edges.
Figure 2. Branches to be disconnected in the system.
Figure 3. Columns to be disconnected from the incidence matrix.
The matrix 
is calculated according to Equation (1.9),
(1.9)
The direct resolution of system (1.9) requires great computational effort, because the matrix 
has the dimension of the number of rows, while 
has the dimension of the number generators. An efficient solution can be obtained with the following step sequence [8] :
Step 1) Consider a matrix
, constituted by matrix 
and canonical vector
, thus 
(note that this matrix is square and non-singular).
Step 2) To matrix 
a row and a column are added, to adjust its dimension to the multiplication among the matrices.
Step 3) From matrix 
the j-th line and j-th column are removed, with j ranging from
, where its intersections cannot be null. Accordingly, we are removing a generation bus from the matrix, its dimension is not changed, and there is only the replacement by zero of the j-th row with zero and column removed.
With this these modifications, the matrices are readjusted, therefore, 
of 
of 
de
, the matrix 
is named 
and rewritten as
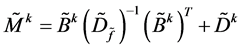, which has the dimension
. Vector 
Step 4) We define:
(1.10)
This system is solved in two steps [11] :
1) We will first solve the following linear systems
It is important to note that we are assuming that in the time intervals 
there are the planned manipulations i;
i.e. the matrices 
and 
vary throughout the interval as a function of the number of manipulations.
The vector 
can be found with ease using, for example, the factorization LU of
, which does not vary along the iterations. In the algebraic form, we write:
.
2) The Sherman-Morrison-Woodbury formula [12] is used for the calculation of the inverse of matrix
:
where 
and 
are matrices of dimension 
and 
has the dimension
. Adapting to our problem, we have 
e
.
Observe that:
• If a diagonal matrix of dimension
, whose elements are those that belong to the matrix
;
• 
is formed by columns from the identity matrix;
• 
.
Therefore, 
is written as:
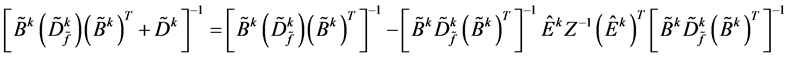
where,
.
Note that 
is a symmetric positive-definite matrix, with dimension equal to the number of generators. Therefore, the calculation of 
is not costly, as the matrix allows the application of Cholesky decomposition and has relatively small dimension.
Multiplying the Sherman-Morrison-Woodbury equation, already applied in this problem by
, we have:
.
Note that the matrices 
can be factored before starting the iterative process, in a similar way to what can be accomplished with matrix
, in the case of the problem without manipulations.
3.5. Bus Manipulations
A bus manipulation occurs when generators or loads are disconnected from the system. The loads have variations that are not always predictable over time, which is a factor that can hinder system modeling.
Unlike line manipulations, in bus manipulations we cannot choose branches that belong, or not, to the spanning tree, because, obviously, when disconnecting a bus, lines from the spanning tree and the additional edges must be disconnected. To prevent damage to the system, we chose to execute manipulations only on buses with a degree of less than two (only one edge of the tree touching it). Again, it is easy to change the heuristic in [6] to get trees with these characteristics.
We assume that n-edges touch on the bus to be operated, then n-rows and columns from 
and one more line from the incidence matrix 
should be removed.
3.6. Solving the Predispatch Problem with Bus Manipulations
The manipulations involving generation buses and loads are similar to line manipulations. But in this case, the study of the matrix structure of the problem associated with these manipulations must also be executed in the spanning tree. When there are bus manipulations at different time intervals, there is a modified network topology. Therefore:
where
.
In this study, we decided to consider only bus manipulations whose modes associated in the tree have a degree of less than two; that is, the manipulations are carried out in the leaf of the tree. This prevents the system from being disconnected, which occurs mostly in small problems. Thus, in Figure 1, the only buses that can be disconnected are 
and
. Assuming that bus 
has been chosen, the changes in the incidence matrix are shown in Figure 4. The columns and row featured must be removed from the matrix.
In the incidence matrix, the columns relating to branches that are connected to the bus will be disconnected. Note that by removing these columns, the incidence matrix is replaced by a null line; therefore, this line is also removed from the matrix.
The changes in the reactance matrix are illustrated in Figure 5.
Note that we simply have to search for the nonzero element in the column of the branches of the additional edges and remove the reactance element associated with it, similar to the case with line manipulations.
This approach to the problem involves no loss of generality. In fact, if necessary, we can manipulate a bus that corresponds to a node of the tree of degree 2.
The next step is to execute line and bus manipulations in the same time interval.
4. Heuristic for the Construction of the Spanning Tree
The purpose of this section is to show the heuristics used for the construction of the spanning trees used in the
Figure 4. Rows and columns to be removed.
Figure 5. Reactance matrix of the system.
experiments performed. In this study, we have opted for the construction of a spanning tree with additional edges. Thus, it is possible to have a reactance matrix whose structure can be effectively exploited.
The reactance matrix is denoted by
, where the sub-matrix 
is diagonal and represents the edges of the co-tree. It is known that the sparseness of the reactance matrix depends on the circuits adopted in its construction. The purpose of the following heuristic is to build a sparse reactance matrix:
• We choose the bus with the higher degree as the root, and all of its neighbors as children;
• The remaining neighbor buses from the greater degree of leaves are then added to the tree;
• The procedure is repeated until all buses are part of the tree.
Thus, we have attempted to build a tree with a small depth. The circuit obtained adding a line that does not belong to the tree and form the reactance matrix. In a shallow tree, these ties tend to contain few buses, resulting in a sparse matrix. Note that each additional edge also belongs to a single circuit; that is, XN is diagonal. Finally, considering that XN is diagonal, the reactance matrix has linearly independent rows and, since there are 
matrix out of the tree, we obtained the number of equations needed to form X [13] .
5. Numerical Experiments
On the implementation of the interior-point methods for the solution of the predispatch problem with manipulations, the matrix structure of the system is modified. In this study, the manipulations are a data input. Thus, the changes that have occurred in the matrices are known before and can be studied before the beginning of the iterative process. Without loss of generality, it is possible to use a heuristic for the construction of the spanning tree, in order to ensure that the branches to be manipulated will always belong to the co-tree [14] .
For both line and bus manipulations, the matrix 
is stored for subsequent calculations of the resolution of linear systems of the interior-point method. On the question of functionality, only the branches that are active in the system are stored, i.e., the columns of the matrix 
which are connected in a specific period of time.
5.1. Test Systems
The networks in which the tests were executed include the IEEE30 and IEEE118 systems representing the American Midwest, and the Brazilian system composed of 1993 and 3511 buses.
The Brazilian system with 3511 buses and 4237 branches corresponds to the operational programming of Brazilian system from 24/Jun/2006.
In the computational experiments executed herein, we used the primal-dual interior-point method and carried out tests with the number of manipulations ranging from zero to six in one day, which is a common occurrence in the Brazilian power system.
The implementation was developed on a 2.5 GHz Intel Core i5 processor, 4 GB 1333 MHz DDR3 memoryMacintosh HD in Matlab 7.0 with accuracy of 
in order to consider the optimal conditions of the problem satisfied.
The tests carried out used the starting point shown in Equation (1.11):
(1.11)
5.2. Computational Results for Line Manipulations
The number of iterations necessary for convergence may vary significantly depending on the branch that is being manipulated. If a branch with a high flow is disconnected, the method will have to find a new way to meet the demand, reflecting on the number of iterations and, consequently, on the computational time. However, other reasons may be responsible for this increase, because depending on the branch that is being manipulated and its resulting network, the adequacy of the system may not be efficient.
For the case with line manipulations, we observe only a small increase in computational time, as shown in Tables 1-6, which is affected not only by the number of manipulations, but also by the branches manipulated.
5.3. Computational Results for Bus Manipulations
Bus manipulations do not cause major modifications in computational results because, when a bus is removed, the system is reduced to a simpler subsystem. The results of Table 7 and Table 8 show that these modifications
Table 1 . IEEE30 system.
Table 2. IEEE118 system.
Table 3. SSECO system with 1654 buses.
Table 4. SSECO system with 1732 buses.
Table 5. BRAZIL system with 1993 buses.
Table 6. BRAZIL system with 3511 buses.
do not result in larger computational costs. In the next section, we will be address the case in which bus and line manipulations are executed simultaneously, then a more interesting analysis in relation to the behavior of the system will be possible.
When compared to the problem that does not consider manipulations, the computational cost per iteration is essentially the same. In addition, there was a small increase in the number of iterations in the problem with manipulations compared to the same problem without considering them.
Table 7. IEEE30 system with bus manipulations.
Table 8. IEEE118 system with bus manipulations.
The efficiency of the methodology used in this study can be proven not only by convergence, but also by nonconvergence in some tests carried out with infeasible systems. Accordingly, we could prove that the implementation actually optimizes the problems addressed.
Accordingly, the model developed approaches the real problem much closer with an insignificant additional computational effort and without presenting any numerical stability problems.
6. Conclusions
In this work, interior-point methods are used to solve a predispatch problem in a hydroelectric system. The contribution of this research is to solve these problems with line and bus manipulations executed simultaneously. When these manipulations occur, the network topology is modified. The characteristics of this problem and its importance for the Brazilian electricity system have motivated the development of this research.
The methodology used in the development of this study is the primal-dual interior-point method, as it presents satisfactory results for problems of optimal power flows.
In order to improve efficiency in the solution of the predispatch problem studied herein, we use a heuristic for the construction of a shallow spanning tree, so the reactance matrix used is sparser.
From the computational point of view, the effort to solve a problem with or without such modifications on the network topology is similar. Even with the modifications in the matrices of the problem, the number of linear systems that need to be solved remains the same, compared to the problem without manipulations. Furthermore, the number of iterations required for convergence of the interior-point method depends on the importance that the manipulated branches and buses have on the system.
The results obtained showed the adequacy of the methodology, both in the numeral aspects and in the times of convergence: the times required to attain the solution were kept below five minutes for the larger problems for implementation in Matlab. However, these times can be dramatically reduced to a few seconds in a high-performance language.
Acknowledgements
This research was partially sponsered by the Foundation for the Support of Research of the State of São Paulo, (FAPESP) and the Brazilian Council for the Development of Science and Technology (CNPq).