1. Introduction
The inherent difficulty in the analysis of a territory as a single unit has been discussed in the classic literature of territorial design (TDP, Territorial Design Problem) [1] . This analysis involves the reduction of the territorial analysis to groups or zones under geographical aggregation using hierarchical grouping or partitioning methods fitting the problem.
For aggregation, this work uses as elements to be grouped the geographic territorial unit known as Basic Geo- Statistical Area (Ageb), defined as the minimum geographic division used for census and statistical purposes. The groups are comprised by a set of Agebs, considering within the grouping the properties of partitioning and the feature of compactness.
Solving geographical aggregation is a necessary task in territorial design problems and has been framed as a combinatorial problem of geographical partitioning or as geographical clustering [2] [3] . The aggregation being solved so far groups Agebs where the implicit objective function evaluates the minimum cost of the distance between them. This problem is discrete and mixed-integer; it has been formulated as a model of combinatorial optimization under the compactness criterion as an objective function where the associated partitioning algorithm is based on the classical partitioning algorithms [4] .
The combinatorial nature of Agebs partitioning involves the use of approximate methods [5] , therefore in solving them, heuristic methods of confirmed efficiency when applied to difficult combinatorial problems have been used: Variable Neighborhood Search (VNS) and Simulated Annealing (SA) [2] [6] .
With the goal of evaluating the quality of solutions from both heuristics and determining which one best approximates the cost function for this problem; a statistical factorial surface response model has been used. Once the efficiency of VNS or SA has been guaranteed, the territory is partitioned in 8 groups to determine the distribution center for the location-allocation problem with dense demand. This Location-Allocation Problem (LAP) for a TDP with dense demand has the objective of finding the geographical coordinates (longitude, latitude) for the location of a Distribution Center (DC) that provides a service to a group of communities contained in each Ageb, which is represented by a centroid. The location of the DC must be the one which minimizes the travel expenses by finding the geographical center coordinates of all centroids. These community populations repre- sent potential clients for the DC and their demand is modeled by a continuous two-variable function based on the population density of each group [7] .
An application of this approach is the location of medical health centers for each community at the centroid of each Ageb and the location of a general hospital at the geographical center of the centroids, which operates as a DC in such a way that a patient transfer requires minimal time. In geographical terms the terrestrial globe, after applying a suitable geographical projection, is considered as a subset of the cartesian plane. In the proposed methodology the solutions are taken as 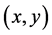 points in
points in  using geographical coordinates, where
using geographical coordinates, where 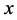 is the longitude coordinate and
is the longitude coordinate and 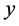 the latitude coordinate. Due to the numeric nature of the obtained solutions, the problem comprises a continuous case of the LAP. In addition to the mathematical formulation of the problem a Geographical Information System (GIS) is used with the purpose of creating maps via spatial data files and to perform information queries on the geographical zones [8] .
the latitude coordinate. Due to the numeric nature of the obtained solutions, the problem comprises a continuous case of the LAP. In addition to the mathematical formulation of the problem a Geographical Information System (GIS) is used with the purpose of creating maps via spatial data files and to perform information queries on the geographical zones [8] .
The structure of this paper is organized as follows: Introduction as Section 1; in Section 2 important aspects of territorial design are covered; the experiment designs methodology is described in Section 3. Section 4 presents a comparison between the response times of VNS and SA. In Section 5, we present our model and methodology for the Location-Allocation Problem. Finally, section 6 deals with the conclusion and future remarks.
2. Territorial Partitioning
In general, the problem of territorial design is defined as the collection of basic geographical units into large groups known as territories. An acceptable grouping is the one which fulfills certain predetermined criteria for a specific territorial design problem. These criteria can be economical, demographical, location-allocation of services, among others [1] . This work requires a territorial grouping, which involves the partitioning of the territory under study. The partitioning of the territory has been the result of implementing an algorithm where the creation of groups is performed based on the property of geometric compactness of territorial design and the minimization of distances between centroids [2] .
2.1. Formulation of the Territorial Partitioning Problem
This section establishes the model for the territorial partitioning problem as a Combinatorial Optimization Problem (COP) as follows: Given a territory 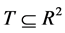 formed by Agebs denoted by
formed by Agebs denoted by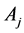 , i.e.
, i.e.
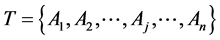 such that
such that 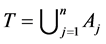 and
and  and let
and let 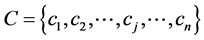 be the set of centroids of each Ageb in
be the set of centroids of each Ageb in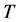 , where
, where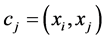 . We want to form a set
. We want to form a set ,
, 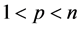 ,
,  such that
such that 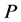 is a partition of
is a partition of ![]() and each
and each ![]() is a collection of Agebs. Under the
is a collection of Agebs. Under the
criterion of geographical compactness the objective function to be minimized consist of the Euclidean distance from one of the ![]() centroids
centroids ![]() to every other centroid
to every other centroid ![]() of the same group
of the same group ![]() and the solution space
and the solution space ![]() is the set of all partitions of
is the set of all partitions of ![]() with cardinality p:
with cardinality p:
![]() (1)
(1)
Equation (1) corresponds to the objective function of the partitioning problem. Note that in the case of a search by exhaustive enumeration in ![]() the number of alternative solutions that must be examined to find the solution is given by
the number of alternative solutions that must be examined to find the solution is given by
![]() (2)
(2)
where ![]() is the number of Agebs and
is the number of Agebs and ![]() is the desired number of groups.
is the desired number of groups.
While Equation (2) suggests that the complexity order is ![]() for
for ![]() and consequently polynomial in
and consequently polynomial in ![]() for a given value of
for a given value of![]() , the number of combinations is quite large [9] .
, the number of combinations is quite large [9] .
![]() (3)
(3)
For variable values of ![]() the problem are still NP-complete since the time required to solve by exhaustive search grows exponentially in
the problem are still NP-complete since the time required to solve by exhaustive search grows exponentially in ![]() this justifies the use of a metaheuristic) [5] .
this justifies the use of a metaheuristic) [5] .
To manage the computational cost, VNS and SA have been implemented. This section examines VNS in detail due to the fact that in the exercise of the statistical experiment, it was proven that VNS responds with better solutions for the territorial partitioning problem exposed in this work (this reason justifies the use of VNS as approximation method).
2.2. Basic Variable Neighborhood Search
The Variable Neighborhood Search (VNS) meta-heuristic has been incorporated to the territorial partitioning problem to obtain approximate solutions. We have abstracted the essential aspects of VNS and Variable Neighborhood Search Descendent (VNSD) to simplify them into a single flexible and easy algorithm to be used in several implementations for partitioning problems as is shown in the following procedure [10] [11] :
Procedure 1. VNS.
Require Number of Structures NS, Local Search LS and Input Instance.
1) ![]() Neighborhood Structures
Neighborhood Structures![]() ,
,![]() ;
;
2) Generation (Initial Solution);
3) For ![]() to NS do;
to NS do;
4) Current Solution ← Local Search ![]() (Initial solution);
(Initial solution);
5) Initial solution ← Current Solution;
6) End for;
7) Best Solution ← Initial solution;
8) Return Best Solution.
The parameters in this procedure include Neighborhood Structures (NS) and Local Search (LS), which are considered to be evaluated by the statistical experiment. It is convenient to review the way that the neighborhoods are generated in VNS from an initial solution. This implementation can be seen in [2] .
3. Experiment Designs to Determine the Parameters in the Metaheuristics
In this work, we have applied factorial designs and response surfaces to evaluate the performance of Variable Neighborhood Search and Simulated Annealing meta-heuristics with the methodology Response Surface.
3.1. Response Surfaces
The Response Surface Methodology (RSM) is a collection of techniques that allow inspecting a response that can be represented by a surface, when the experiments explore the effect of the variation of quantitative factors in the values of a dependent variable or response variable [12] . This methodology tries to find the optimal values for the independent variables to maximize, to minimize or just to meet some constraints in the response variable. The trend in the development of RSM has been the construction of compact designs of experiments, with a minimum of experimental designs. Thus the researcher focuses in the properties of the estimators of all the parameters of the response function, which depend on the type of design used.
To estimate a response surface, the linear models of order less than or equal to three have been employed frequently because of their simplicity and easy interpretation. However, [13] show that the fractional polynomials can make a better approximation in some experiments. The bases of the RSM are obtained from the theory of the general linear model. It is assumed that the response variable depends on the independent variables through a function ![]() that can be complex or unknown. The function is approximated in the region of interest by a polynomial of low order, generally less than or equal to three, or pseudo-quadratic. To evaluate the efficiency of the estimators of a response surface several procedures have been proposed based on the bias. This is the case of the mean square error (MSE) that also has been taken as a base to obtain others like that proposed by [14] . There are several classes of designs developed for the approximation of a surface of second order that require less combinations of treatments than the factorial designs, with different characteristics and properties. Among these, the central composite designs proposed by [12] do not grow as fast as the factorial designs or the Box-Behnken designs.
that can be complex or unknown. The function is approximated in the region of interest by a polynomial of low order, generally less than or equal to three, or pseudo-quadratic. To evaluate the efficiency of the estimators of a response surface several procedures have been proposed based on the bias. This is the case of the mean square error (MSE) that also has been taken as a base to obtain others like that proposed by [14] . There are several classes of designs developed for the approximation of a surface of second order that require less combinations of treatments than the factorial designs, with different characteristics and properties. Among these, the central composite designs proposed by [12] do not grow as fast as the factorial designs or the Box-Behnken designs.
3.2. Central Composite Design
We use central composite designs to study the Variable Neighborhood Search metaheuristic. The factors are codified since it is easier to work with the levels of codified factors in a uniform framework to analyze the effects of the factors. The levels of the codified factors in a ![]() factorial design are
factorial design are
![]()
where ![]() is the
is the ![]() level of the factor
level of the factor![]() ,
, ![]() is the average level of factor
is the average level of factor ![]() and
and ![]() [15] .
[15] .
The central composite designs are designs of ![]() factorial treatments with
factorial treatments with ![]() additional combinations called axial points and
additional combinations called axial points and ![]() center points. The coordinates of the axial points of the axes of the codified factor are
center points. The coordinates of the axial points of the axes of the codified factor are ![]() and the center points have the form
and the center points have the form![]() . Depending on the election of
. Depending on the election of ![]() in the axial points, the central composite design has different properties such as orthogonality, rotatability and uniformity. We will consider only one desirable property in these designs that requires the variance of the estimated values to be a constant in equidistant points from the center of the design.
in the axial points, the central composite design has different properties such as orthogonality, rotatability and uniformity. We will consider only one desirable property in these designs that requires the variance of the estimated values to be a constant in equidistant points from the center of the design.
This property is called rotatability, and is achieved making![]() . In this way, the value of
. In this way, the value of ![]() or design
or design
with two factors is ![]() and for three factors
and for three factors![]() . The formula for
. The formula for ![]() changes if replicates of the design are done or if a fractional factorial design is used [16] .
changes if replicates of the design are done or if a fractional factorial design is used [16] .
3.3. Determination of VNS and SA Parameters for the Territorial Partitioning Problem
In this section, the statistical procedure that has been followed to get adequate parameters for the heuristics to compare is exposed. For VNS the application of a central composite design is proposed and for SA a Box Behnken. Finally, the needed tests are done to model the parameters and finding adjusted times in order to be able to compare the two heuristics in an unbiased way when the time (T, seconds) has been chosen as a colleting parameter.
VNS Parameters for the Territorial Partitioning Problem under a Central Composite Design
The VNS implementation in territorial partitioning pursues an analysis of the behavior of the algorithm. In this point certain results have already been reported where VNS parameters NS and LS have been modulated for ins- tances of 24 groups [2] . For purposes of this paper, 8 groups have been considered as representative instance under study. The goodness of the factorial statistical methodology applied in the calibration of the VNS para- meters ensures their usefulness in this work.
We have started with the study over a set of tests to prove the general functionality: the response time must considerably reduce the computational cost and the quality of the solutions must be very close to the optimal. Due to the fact that we are interested in adjusting the VNS parameters to set the time as the comparison factor with SA, in this first experiment the cost function is just the time (T, seconds).
Previous studies have been revised to build diverse experiments with the goal of finding strategic values for the proposal of an experimental design that provides the balance of competitive parameters for VNS [2] .
A composite central design was used with a high level of 1718 and 1365 as the low level for neighborhood structures (NS). In Local Search (LS) 1031 has been determined as the low level and 1370 as the high level.
The associated experiment can be seen in the next Table 1 and Figure 1 attached indicates that the data behaves normally, that the second order model is adequate and that there’s no effect between runs in the experi- ment. The regression model of second order exits statistical evidence for the reliability of the experiment:
3.4. Simulated Annealing Parameters Determination for the Territorial Partitioning Problem with Box Behnken
The Box Behnken (BB) design is an independent quadratic design that doesn’t possess a factorial or a fractional factorial design. These designs are revolving (or almost revolving) but they possess limited capacity of orthogonal blocking compared with the Central Composite Design (CCD).
The Box Behnken Design for 3 factors involves 3 blocks, in each one of them 2 factors are varied through the 4 possible high and low combinations. Is furthermore necessary to include central points, where all of the factors are in their central values. In consequence, these designs don’t contain points in the vertex of the experimental region. The number of experiments required ![]() is defined by the expression
is defined by the expression
![]()
where ![]() is the number of factors and
is the number of factors and ![]() is the number of central points [16] .
is the number of central points [16] .
Simulated Annealing
Simulated Annealing (SA) is a neighborhood search algorithm with probabilistic criteria to accept solutions based on thermodynamics, is a neighborhood search method characterized by a neighboring solutions accep- tance criterion that adapts along its execution. In general, SA is a metaheuristic which combines the principles of the basic local search and the probabilistic Monte Carlo approach [6] .
The temperature ![]() is important in SA and determines in what measure worse neighboring solutions than the current can be accepted. The variable
is important in SA and determines in what measure worse neighboring solutions than the current can be accepted. The variable ![]() is initialized with a high value, denominated initial temperature
is initialized with a high value, denominated initial temperature
![]() and is reduced in every iteration by means of a cooling mechanism (alpha), until a final temperature
and is reduced in every iteration by means of a cooling mechanism (alpha), until a final temperature ![]() is reached. In each iteration a concrete number of neighbors,
is reached. In each iteration a concrete number of neighbors, ![]() is generated that can be fixed for all of the execution or depend on the concrete iteration [6] . In this work
is generated that can be fixed for all of the execution or depend on the concrete iteration [6] . In this work ![]() has been denoted by
has been denoted by![]() .
.
We are betting on determining values in the SA parameters so they can be compared in a fair way with VNS, being the time ![]() of execution the common parameter for the 2 heuristics under study. To get close to convenient parameters, the first part of the tests was experimental and random. Considering the times obtained in the Table 1 for VNS, diverse instances were created for SA relying on their respective BB (to trust in the suitability of the model). The next design was achieved and its model and instances can be seen in the Table 2 and the Figure 2 shows that the data behaves normally and that there’s no effect between runs in the experi- ment:
of execution the common parameter for the 2 heuristics under study. To get close to convenient parameters, the first part of the tests was experimental and random. Considering the times obtained in the Table 1 for VNS, diverse instances were created for SA relying on their respective BB (to trust in the suitability of the model). The next design was achieved and its model and instances can be seen in the Table 2 and the Figure 2 shows that the data behaves normally and that there’s no effect between runs in the experi- ment:
4. Modeling of the Response Times for VNS and SA in Instances of 8 Groups
Reviewing Section 3 and after having carried out the corresponding runs for SA and VNS, it is necessary to model the associated parameters to calibrate them in such a way that is possible to optimize the response time, which will be in function of the values of the parameters.
4.1. Modeling of the Response Times for VNS
Gathering the results obtained for VNS (see Table 1 and Figure 1), contour graphs have been used that reflect in another way the response surface. Different variations of the parameters were done and we chose a represent- ative contour graph to optimize distinct units of times ![]() estimated in seconds: 275, 285, 290, 300, 310, 320, 330 and 340. Among different tests with the contour plot [2] , we chose the best result: the time should be be- tween 280 and 340 seconds while the values for Local Search (LS) are between 1050 and 1350 iterations, and Neighborhood Structures (NS) bounded by 1400 and 1750 iterations. With this values it has been possible reach the compromise now is to get the exact parameters to run VNS in the established times, then, under the model of second order, graphs were obtained that reflect the measure of the parameters to obtain the Cost Function (CF), that in this case is the time. The optimization graphs are presented for the cases of 275 seconds (see Figure 3, where
estimated in seconds: 275, 285, 290, 300, 310, 320, 330 and 340. Among different tests with the contour plot [2] , we chose the best result: the time should be be- tween 280 and 340 seconds while the values for Local Search (LS) are between 1050 and 1350 iterations, and Neighborhood Structures (NS) bounded by 1400 and 1750 iterations. With this values it has been possible reach the compromise now is to get the exact parameters to run VNS in the established times, then, under the model of second order, graphs were obtained that reflect the measure of the parameters to obtain the Cost Function (CF), that in this case is the time. The optimization graphs are presented for the cases of 275 seconds (see Figure 3, where![]() ,
, ![]() and
and![]() ).
).
4.2. Modeling of the Response Times for SA in Instances of 8 Groups
From the results achieved for SA (see Table 2), diverse contour graphs were done. A contour graph was picked, that as well as VNS, shows distinct units of times ![]() estimated in seconds: 275, 285, 290, 300, 310, 320, 330 and 340 and the parameters of
estimated in seconds: 275, 285, 290, 300, 310, 320, 330 and 340 and the parameters of ![]() and
and ![]() are fixed at 0.98 and 3000 units respectively.
are fixed at 0.98 and 3000 units respectively. ![]() is between 0.90 and 0.110 while
is between 0.90 and 0.110 while ![]() oscillates in 8200 and 9800 units (iterations). Relying on all of the results obtained until now and with the model of second order, is possible to create a model to find a balance of the SA parameters and to reach a cost for the selected times. In the graphic of optimization showed in Figure 4, the calibration of the parameters can be seen to obtain a cost function of 285 seconds. The notation in this Figure 4 is
oscillates in 8200 and 9800 units (iterations). Relying on all of the results obtained until now and with the model of second order, is possible to create a model to find a balance of the SA parameters and to reach a cost for the selected times. In the graphic of optimization showed in Figure 4, the calibration of the parameters can be seen to obtain a cost function of 285 seconds. The notation in this Figure 4 is![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
![]()
Figure 3. Optimizer for VNS (T275 seconds).
![]()
Figure 4. Optimizer for SA (T285 seconds).
4.3. Response Times Comparison
The challenge at this point is to check that VNS and SA execute within the time we have found where both heuristics must run in the same time when the parameters have indicated the time in which they must execute for determined values. The next step consist in doing the associated tests and verifying that with calibration of the parameters for SA and VNS they achieve a cost function in a determined time, in this way we can observe which heuristic offers better quality in the solutions.
In Table 3, the values of the Objective Function (OF) and the cpu time (![]() ) have been recorded for the parameters of VNS suggested by the statistical model that has been developed. It is clear to note that the real computing times (
) have been recorded for the parameters of VNS suggested by the statistical model that has been developed. It is clear to note that the real computing times (![]() ) are almost “exact” with the ones estimated by the model.
) are almost “exact” with the ones estimated by the model.
In a similar form, in Table 4 the values of the objective function and the ![]() time have been ordered for the parameters of SA given by the statistical model that has been developed. The real computing times are much approximated with the ones estimated by the model.
time have been ordered for the parameters of SA given by the statistical model that has been developed. The real computing times are much approximated with the ones estimated by the model.
Finally, the results of the times and objective function for SA and VNS were gathered. In Table 5, it can be observed that VNS reaches better values of the cost function in instances of 8 groups.
Having obtained these results, our interest now is to solve the aspect of the dense demand.
The best cost of the OF for VNS has been chosen and to initiate the study with parameters of neighborhood structure ![]() and local search
and local search![]() .
.
![]()
Table 3. Times for the VNS experiment.
![]()
Table 4. Times for the SA experiment.
![]()
Table 5. Times and OF for SA and VNS.
5. Model and Methodology for Location Allocation Problem
This section describes the mathematical model and the basic methodology to solve the location-allocation problem for a territorial design problem with dense demand.
The Location-Allocation Problem will be denoted as LAP. The LAP is an optimization problem, classic in the location theory that is often used in territorial design problems TDP. With the Agebs well defined when solving it, the location of the facilities is determined and the clients are allocated to each facility. The territorial design problem can be studied by means of the P-Median Problem that we'll denote as PMP. The location-allocation problem belongs to the problems class NP-complete [5] . The problem solved in this work gives answer to the problem of locating facilities and allocating clients in dense demand scenarios in TDP. The computing complexity of PMP makes necessary the appliance of a metaheuristic as approximation procedure to the optimal solution.
The development of the proposal of the p-median problem had place in the 60’s and the direct case can be attributed to Hakimi and to Weber, the continuous case [9] [17] . The p-median consists of a given set of ![]() vertices and a distances (or costs) matrix between the vertices,
vertices and a distances (or costs) matrix between the vertices, ![]() vertices must be chosen with the purpose to minimize the sum of the distances of all the points to the closest chosen selected point. In 1970, the first integer programming formulation for the p-median problem is presented, cited in [17] . In general, the P-Median Problem can be mathematically expressed as a discrete optimization problem. First we denote the distances matrix as
vertices must be chosen with the purpose to minimize the sum of the distances of all the points to the closest chosen selected point. In 1970, the first integer programming formulation for the p-median problem is presented, cited in [17] . In general, the P-Median Problem can be mathematically expressed as a discrete optimization problem. First we denote the distances matrix as ![]() that expresses the distance between the potential location points
that expresses the distance between the potential location points ![]() and the demand points
and the demand points![]() . Two binary variables are introduced, the first one
. Two binary variables are introduced, the first one ![]() corresponds to the location of the demand point
corresponds to the location of the demand point ![]() to the facility
to the facility ![]() or not and the second
or not and the second ![]() indicates that a facility is established in the point
indicates that a facility is established in the point ![]() or not, and can be proposed as a binary integer problem in the following way:
or not, and can be proposed as a binary integer problem in the following way:
Let
![]()
and
![]()
![]() (4)
(4)
Subject to
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
where ![]() is the distance between the centroid
is the distance between the centroid ![]() and the Ageb
and the Ageb ![]() and
and ![]() is the number of potential vertices where a median can be located, generally
is the number of potential vertices where a median can be located, generally ![]() is the fixed number of required medians. Equation (4) is the objective function that minimizes the system’s distance, the restriction 5 establishes that each demand point can only be allocated to one facility. The restriction 6 establishes the allocation of demand points to each of the facilities or medians and finally the restriction 7 guarantees that among the
is the fixed number of required medians. Equation (4) is the objective function that minimizes the system’s distance, the restriction 5 establishes that each demand point can only be allocated to one facility. The restriction 6 establishes the allocation of demand points to each of the facilities or medians and finally the restriction 7 guarantees that among the ![]() potential location points exactly
potential location points exactly ![]() are chosen.
are chosen.
Given a set of customers spread over a territory![]() ,
, ![]() a partition of
a partition of ![]() in
in ![]() groups, each
groups, each ![]() ,
, ![]() and
and ![]() a partition of each element of
a partition of each element of ![]() in
in
Agebs. Each ![]() has a representative called centroid Ageb denoted by
has a representative called centroid Ageb denoted by ![]() obtained by the formulas (11) from which each community is served. Each point
obtained by the formulas (11) from which each community is served. Each point![]() , has a density of demand given by
, has a density of demand given by![]() . Let
. Let ![]() be the Euclidean distance from any point
be the Euclidean distance from any point ![]() to the centroid. The cost of transportation from a point
to the centroid. The cost of transportation from a point ![]() to the centroid
to the centroid ![]() is defined as
is defined as![]() .
.
The solution consists in finding the coordinates from a point ![]() such that the cost of the transporta-
such that the cost of the transporta-
tion is minimized from each community to a central facility. The conditions to be satisfied by forming joint par-
titions of ![]() and of
and of ![]() are that they are disjoint, namely
are that they are disjoint, namely ![]() and
and![]() ,
, ![]() and
and![]() .
.
The mathematical model that represents the mentioned conditions is the following:
![]() (8)
(8)
Subject to
![]() (9)
(9)
![]() (10)
(10)
The objective function TC represented in Equation (8) is the total cost of transportation, and Equations (9) and (10), are the constraints of the partitioning of the territory ![]() and the
and the![]() . But in practice we define the instances under the general PMP definition as POC and also its instance as follows:
. But in practice we define the instances under the general PMP definition as POC and also its instance as follows:
Given a set ![]() of potential facilities and a set
of potential facilities and a set ![]() of
of ![]() users, a matrix
users, a matrix
![]()
where ![]() represents the euclidean distance between users
represents the euclidean distance between users ![]() and the facilities
and the facilities![]() ,
, ![]() , a predefined
, a predefined![]() , then an instance of PMP is denoted by
, then an instance of PMP is denoted by![]() .
.
A feasible solution for ![]() is a subset
is a subset![]() ,
, ![]() , which cost function is defined by
, which cost function is defined by
![]() .
.
The objective of PMP is to find a feasible solution ![]() such that
such that
![]()
where ![]() is the set of all the feasible solutions.
is the set of all the feasible solutions.
The PMP consists in determining simultaneously the positions of ![]() in which the
in which the ![]() services must be located, in such a way that the total transport cost necessary to satisfy the demands of the users is minimized, supposing that said cost is proportional to the amount of demand and the traveled distance. For that, each user will be attended by the closest plant or service.
services must be located, in such a way that the total transport cost necessary to satisfy the demands of the users is minimized, supposing that said cost is proportional to the amount of demand and the traveled distance. For that, each user will be attended by the closest plant or service.
The sequence of necessary steps to obtain the coordinates of the central facility in a cluster is as follows:
Define the parameters for the partitioning of the territory![]() .
.
Generate the partitioning with the VNS metaheuristic.
With the file obtained from step 2, generate a map within a map using a GIS.
Associate a density of demand function ![]() to the chosen cluster
to the chosen cluster![]() ,
,![]() .
.
Calculate the centroids of each AGEB, using calculus Formulas (11).
Apply the Equation (8) to the chosen cluster.
![]() (11)
(11)
Equations (11) are the classical calculus formulas used to calculate the centroid of a metallic plate with density ![]() [18] . In this paper, we consider the Agebs as if they were metallic plates with population density given by
[18] . In this paper, we consider the Agebs as if they were metallic plates with population density given by![]() .
.
5.1. Response Surfaces
In this subsection, the proposed methodology has been implemented for the Metropolitan Zone Toluca Valley (MZTV).
Having partitioned the territory in 8 groups, we select one of the clusters to apply the experiment and this consists of obtaining the centroid for each Ageb, and then calculating the center of the centroids. Finally, the results of the implementation are shown.
Implementation of the Methodology to the Metropolitan Zone Toluca Valley
For the implementation, is necessary to have the data that describes the MZTV as a geographical area, as well as to have a geographical partition that represents the particular problem. The partition of the MZTV consists of the formation of five clusters of Agebs, according to the criteria of compactness of the clusters. The method in this section has been characterized as TDP. Furthermore, it is a COP classified as NP-complete and is therefore advisable to apply a metaheuristic, as we mentioned in Section 2. Basically, the sequential strategy to resolve the case study in this paper is to follow six steps.
1) The partition parameters are defined. The input to the VNS program is a file that contains the geographical data of the MZTV. The number of clusters to be formed, the number of VNS iterations, and the number of iterations of the local search are introduced.
2) The VNS program is run to obtain a file that contains the Agebs of each of the clusters that make up the MZTV, as well as the run time and the cost associated with the partition.
3) With the exit file of step 2, a map is generated. The map contains the partition corresponding to the running of the VNS program for the MZVT.
4) A cluster of the partition is selected. For our case study, we select one cluster. The Ageb codes are in the first column of Table 6. We associate a density of demand function to this cluster. This function is taken one at a time from the set of six linear functions, and two non-linear ones from Table 7, denoted by LD1, LD2, LD3, LD4, LD5, LD6 y NLD1, NLD2 respectively, and proposed by Murat [19] .
5) The file, with the codes of the Agebs of the MZTV is introduced into a GIS to obtain a map.
6) Finally, the coordinates for the center of the centroids are obtained by applying the model.
Table 6 shows the results that were obtained from the sequential program designed for VNS on the geographical data of the MZTV for each density of demand function associated with the Agebs. To obtain the geographical coordinates of the center of the centroids, a non-linear programming problem was resolved using the optimization tool Solver Excel.
Table 8 shows the results of eight different density functions, arranged in rows and columns in the following way: the first column corresponds to the objective function![]() , that is defined as the product of the function of density of demand, multiplied by the distance from the point
, that is defined as the product of the function of density of demand, multiplied by the distance from the point ![]() to each centroid
to each centroid![]() , in the second and third columns are the decimal coordinates of the center of the centroids. The objective functions used in this work are convex functions.
, in the second and third columns are the decimal coordinates of the center of the centroids. The objective functions used in this work are convex functions.
Figure 5 is the selected group under study (blue circle).
The results in columns 3 and 4 in Table 8 show the coordinates of eight possible points to locate the center of centroids. These points are associated to different functions of demand density for the MZTV instance. Figure 6 presents the location of nine points, where eight of them belong to the coordinates in Table 8. Since the distance between those eight points is negligible, we may choose any point as the center of centroids. It can be observed that the differences in the forms of the demand density functions have a minimal effect in the location of the center of centroids. The red point in Figure 6 with coordinates![]() , red
, red
![]()
Table 6. Key Agebs and coordinates of centroids.
![]()
Table 7. Set of density of demand functions.
![]()
Figure 6. Location of nine points, where eight of them belong to the coordinates in Table 8.
![]()
Table 8. Times and OF for SA and VNS.
point, is calculated as the point with minimal distance to the other eight points and we may name it as the center of centers.
This point is a good choice for the location of the center of centroids of the instance, fulfilling a good compromise with the eight functions proposed for the demand density. Without losing generality we may say that the location of the center may be any point into the circle defined by
![]()
where![]() .
.
6. Conclusion
The proposal in this work is a structure to solve location-allocation models based on Geographic Information Systems. The application is shown in the case study of the MZTV map. The methodology was tested in demand regions with irregular forms in comparison with previous works where regions are rectangular or convex polygons. Since the territory design problem is a hard combinatorial optimization problem, the use of metaheuristics allows obtaining a solution in areas or large size and partitions of high cardinality. According to the analysis of the results obtained, the integration of territorial design aspects with density functions in location-allocation models creates a wider range of possible applications to real problems, for example in supply chain design among others. Therefore, an important contribution of this work is the successful combination of three relevant aspects in real problems: territorial design, location-allocation decisions, and demand density functions. The assembly of several tools like metaheuristics, information systems and mathematical models provides a robust device for application in visual environments, like maps, for the analysis of geo-statistical information.