The Collinear Libration Points in the Elliptic R3BP with a Triaxial Primary and an Oblate Secondary ()
1. Introduction
The famous restricted three-body problem (R3PB) has been receiving considerable attention of scientists and astronomers because of its application in the dynamics of the solar and stellar systems, lunar theory and planetary sciences [1] -[4] . It concerns the motion of an infinitesimal mass under the gravitational influence of two finite masses, called the primaries, which move in circular orbits about their common center of mass on account of their mutual attraction. The solution to this type of problem which has been developed over the centuries from Lagrange [5] -[10] and others, form the basis of the study of the dynamics of celestial bodies, from the computation of the ephemerides to the recent advances in flight dynamics. The original formulation of the circular restricted three-body problem (CR3BP) was based on the approximate circular motion of the planets around the sun and the small masses of the satellites of planets and asteroids compared to the planets’ masses. The orbits of most celestial bodies are however elliptic rather than circular, as such, the ER3BP analyses the dynamical systems more accurately. It possesses five coplanar equilibrium points: three collinear and two triangular, where the gravitational and centrifugal forces just balance each other. The collinear points are generally unstable, while the triangular points are conditionally stable. Their stability occurs in spite of the fact that the potential energy has a maximum rather than a minimum at the latter points.
The ER3BP generalizes the original CR3BP, and improves its applicability, while some outstanding and useful properties of the circular model still hold true or can be adapted to the elliptic case. In particular, possible positions of equilibrium occur when the three bodies form equilateral triangles. An application of this model can be seen in the motion of the Trojan asteroids around the triangular point
. The asteroids in this case are only influenced by the gravitational forces of the Sun and Jupiter, and the orbit of Jupiter around the Sun is assumed to be a fixed ellipse. The influence of the eccentricity of the orbits of the primary bodies on the existence of the equilibrium points and their stability has been the subject of a number of communications [11] -[26] . The families of symmetric-periodic orbits in the three-dimensional elliptic problem with a variation of the mass ratio μ and the eccentricity e were studied by Sarris (1989). In the last year, Singh and Umar [25] investigated the effects of the luminosity and oblateness of both primary bodies on the collinear libration points of the binary systems Achird, Luyten 726-8, Kruger 60, Alpha Centauri AB and Xi Bootis moving in elliptic orbits around their common centre of mass. Recently, Singh and Umar [27] have examined the collinear points of the ER3BP with a triaxial bigger primary.
The bodies in the R3BP are strictly spherical in shape, but in nature, celestial bodies are not perfect spheres. They are either oblate or triaxial. The Earth, Jupiter, Saturn, Regulus, Neutron stars and black dwarfs are oblate spheroids [28] -[33] . The Moon, Pluto and its moon Charon are triaxial. The lack of sphericity, triaxiality or oblateness of the celestial bodies causes large perturbations from a two-body orbit. This inspired several researchers [34] -[38] to include non sphericity of the bodies in their studies of the R3BP.
Our aim is to study the effect of the triaxiality of the bigger primary and oblateness of the smaller one on the positions and stability of the collinear libration points. This system can be applied to the Earth-Moon system and to double pulsars. This paper is organized as follows: in Section 2, the governing equations of motion are presented; Section 3 describes the positions of the collinear points, while their linear stability is analyzed in Section 4; finally Section 5 concludes the paper.
2. Equations of Motion
The equations of motion of a dust grain particle in the ER3BP with a triaxial primary and an oblate secondary in dimensionless-pulsating coordinate system (ξ, η, ζ) are given by
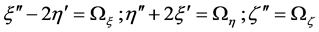(1)
with the force function
(2)
and
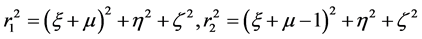(3)
and the mean motion
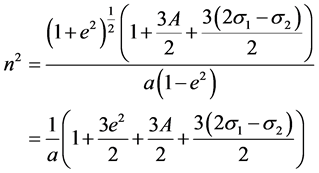(4)
where the prime represents differentiation w.r.t. the eccentric anomaly e and ri (i = 1, 2) are the distances between the third body and the primaries; n, a, e, A and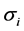 
are the mean motion, semi-major axis; eccentricities of the orbits; oblateness and triaxiality factors respectively.
3. Positions of Collinear Points
The collinear points are the solutions of equations Ωξ = Ωη = Ωζ = 0 and η = ζ = 0; i.e.
(5)
From Equation (3), with η = ζ = 0 and the first of Equation (5), we have
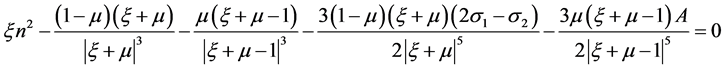(6)
To locate the collinear points on the ξ-axis, we divide the orbital plane into three parts; ξ < ξ1, ξ1 < ξ < ξ2 and ξ2 < ξ with respect to the primaries.
3.1. Position of L1 (ξ wang#Bracket## ξ1)
Let
.
Since the distance between the primaries is unity, i.e.
(7)
Now, substituting Equation (7) in Equation (6) and clearing the fractions, we obtain
(8)
Solving, we get
(9)
3.2. Position of L2 (ξ1 wang#Bracket## ξ < ξ2)
Now,
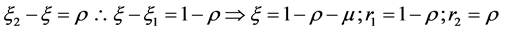(10)
Equation (10) in (6) yields,
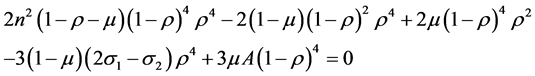(11)
Solving, we get
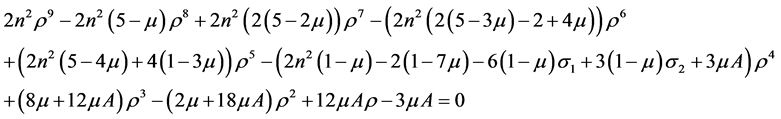(12)
3.3. Position of L3 (ξ2 < ξ)
Since
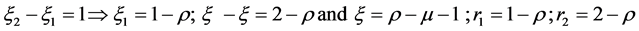(13)
Substituting Equation (13) in (6) and solving, we obtain
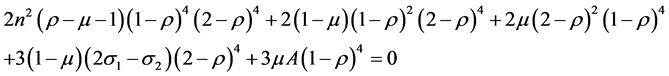(14)
Equations (9), (12) and (14) are seventh degree equations and according to Descartes’ rule of sign, there exist only one real root each corresponding to the three collinear points
. Using Equation (11), we show the effect of triaxiality on the position of L2 for constant oblateness A = 0.001; a = 1.2, e = 0.25, μ = 0.35.
It is seen from Table 1 that, the position of L2 as triaxiality decreases is a shift away from the origin (λ3). This is shown in Figure 1 and Figure 2, for σ1, σ2, λ1, λ2, λ3 and σ1, σ2, λ3 respectively. An interesting result of the numerical computation is the existence of three real roots when σ1 = σ2 = 0.04 (i.e. oblateness of the primary) and σ1 = 0.04; σ2 = 0.03.
4. Stability of Collinear Points
In order to study the stability of the collinear points, we consider the characteristic equation of the system [23] given by
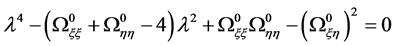(15)
The second partial derivatives are:
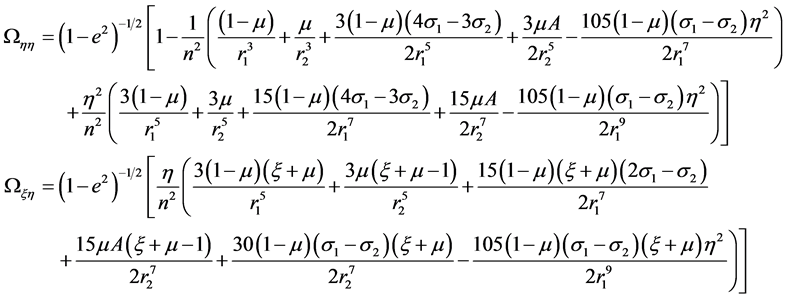
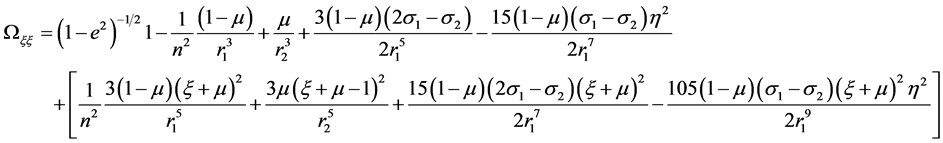(16)
Considering the last interval, ξ2 < ξ.
The collinear points exist on the ξ-axis, i.e. η = ζ = 0, which means
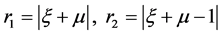(17)
Equation (17) in the first of (16) gives
Table 1. Effect of triaxiality on the position of the inner collinear point L2.
Figure 1. Effect of triaxiality on the position of the inner collinear point L2.
Figure 2. Effect of triaxiality on the position of the inner collinear point L2.
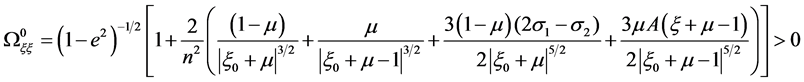
From the second and third of Equation (16) with η = 0, we get
and
. The first of Equation (5) with η = 0, can be written as
(18)
Using Equation (18),
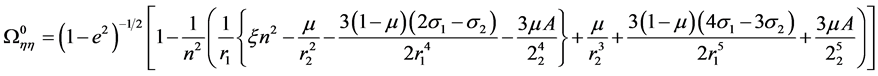(19)
but, 
, which on substitution in Equation (19), yields
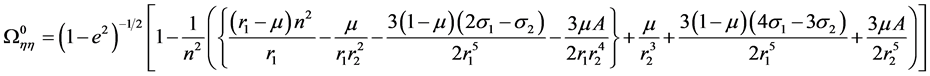
Neglecting higher order terms in e2, a, A and σi (i = 1, 2), we get
Since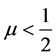 
and
, r1 > 1, r2 < 1,
Also, the last of Equation (16) by virtue of η = 0 gives
.
Similarly, for the collinear points lying in (ξ1 < ξ < ξ2) and (ξ < ξ1),
Since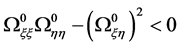 
the discriminant of Equation (15) is positive and its roots can expressed as 
and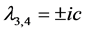
, where b and c are real numbers, thus, the solution is unstable. We may therefore conclude that the stability of the collinear points does not change despite of perturbations on account of triaxiality and oblateness introduced.
6. Conclusion
The positions of the collinear equilibrium points when the primary is a triaxial rigid body and the secondary is an oblate spheroid have been obtained (Equations (9), (12), (14) and Figure 1 and Figure 2). They are seen to be affected by the shape of the participating bodies and their orbital geometries. These results agree with [27] in the absence of oblateness and with [37] in the circular case. The collinear points also remain unstable due to the presence of real roots and despite the introduction of the triaxiality and oblateness parameters.