1. Introduction
Many scientists wish to find appropriate solutions to some mathematical problems that cannot be solved by traditional methods. These problems lie in the fact that traditional methods cannot solve the problems of uncertainty in economy, engineering, medicine and the problems of decision-making and others. One of these solutions is fuzzy sets—the title of Zadeh’s first article about his new mathematical theory, which was published in a scientific journal in 1965. Since Zadeh published his new classic paper almost fifty years ago, fuzzy set theory has received more and more attention from researchers in wide range of scientific areas, especially in the past few years. The difference between a binary set and a fuzzy set is that in a “normal” set every element is either a member or a non-member of the set. Here, we see that it either has to be A or not A. In a fuzzy set, an element can be a member of a set to some degree and at the same time a non-member to some degree of the same set. In classical set theory, the membership of elements in a set is assessed in binary terms according to a bivalent condition an element either belongs or does not belong to the set. By contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set; this is described with the aid of a membership function valued in the closed unit interval [0,1]. Fuzzy sets generalise classical sets, since the indicator functions of classical sets are special cases of the membership functions of fuzzy sets, if the latter only take values 0 or 1. Therefore, a fuzzy set A in a universe of discourse X is a function , usually this function is referred to as the membership function and denoted by
, usually this function is referred to as the membership function and denoted by . Some mathematicians use the notation
. Some mathematicians use the notation  to denote the membership function instead of
to denote the membership function instead of . A fuzzy set A is written symbolically in various
. A fuzzy set A is written symbolically in various

Molodtsov [1] initiated the concept of soft set theory as a mathematical tool for dealing with uncertainties. After Molodtsov’s work, some operations and application of soft sets were studied by Chen et al. [2] , Maji et al. [3] and Maji et al. [4] . Also Maji et al. [5] have introduced the concept of fuzzy soft set, a more general concept, which is a combination of fuzzy set and soft set and studied its properties and also Roy and Maji [6] used this theory to solve some decision making problems. Alkhazaleh et al. [7] introduced the concept of soft multisets as a generalization of soft set. They also defined the concepts of fuzzy parameterized interval-valued fuzzy soft set [8] and possibility fuzzy soft set [9] and gave their applications in decision making and medical diagnosis. Alkhazaleh and Salleh [10] introduced the concept of a soft expert set, where the user can know the opinion of all experts in one model without any operations. Even after any operation the user can know the opinion of all experts. So in this paper, we introduce the concept of a fuzzy soft expert set, which will be more effective and useful which is a combination of fuzzy set and soft expert set. We also define its basic operations, namely complement, union, intersection, AND and OR and study their properties. We give an application of this concept in decision making problem. Finally, we study a mapping on fuzzy soft expert classes and its properties.
2. Preliminaries
In this section, we recall some basic notions related to this work. Molodtsov defined soft set in the following way. Let U be a universe and E be a set of parameters. Let  denote the power set of U and
denote the power set of U and .
.
Definition 1 [1] A pair 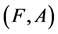 is called a soft set over U where F is a mapping
is called a soft set over U where F is a mapping 
In other words, a soft set over U is a parameterized family of subsets of the universe U For 
 may be considered as the set of
may be considered as the set of  -approximate elements of the soft set
-approximate elements of the soft set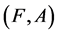 .
.
Definition 2 [5] Let U be an initial universal set and let  be a set of parameters. Let
be a set of parameters. Let  denote the power set of all fuzzy subsets of
denote the power set of all fuzzy subsets of . Let
. Let  A pair
A pair 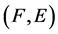 is called a fuzzy soft set over U where F is a mapping given by
is called a fuzzy soft set over U where F is a mapping given by

Let U be a universe, E a set of parameters, X a set of experts (agents), and O a set of opinions. Let Z = E × X × O and .
.
Definition 3 [10] A pair 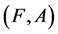 is called a soft expert set over
is called a soft expert set over  where
where  is a mapping given by
is a mapping given by

where  denotes the power set of
denotes the power set of 
Definition 4 [10] For two soft expert sets  and
and  over U,
over U,  is called a soft expert subset of
is called a soft expert subset of  if 1.
if 1. 
2. 
This relationship is denoted by . In this case
. In this case  is called a soft expert superset of
is called a soft expert superset of .
.
Definition 5 [10] Two soft expert sets  and
and  over U are said to be equal if
over U are said to be equal if 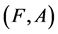 is a soft expert subset of
is a soft expert subset of  and
and  is a soft expert subset of
is a soft expert subset of 
Definition 6 [10] Let  be a set of parameters and X a set of experts. The NOT set of
be a set of parameters and X a set of experts. The NOT set of , denoted by
, denoted by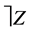 , is defined by
, is defined by 
Definition 7 [10] An agree-soft expert set  over U is a soft expert subset of
over U is a soft expert subset of 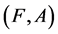 defined as follows:
defined as follows:

Definition 8 [10] A disagree-soft expert set  over
over  is a soft expert subset of
is a soft expert subset of  defined as follows:
defined as follows:

Definition 9 [10] The complement of a soft expert set  is denoted by
is denoted by  and is defined by
and is defined by  where
where  is a mapping given by
is a mapping given by

Definition 10 [10] The union of two soft expert sets  and
and  over U, denoted by
over U, denoted by  , is the soft expert set
, is the soft expert set  where
where  and
and 

Definition 11 [10] The intersection of two soft expert sets 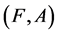 and
and  over U, denoted by
over U, denoted by  , is the soft expert set
, is the soft expert set  where
where 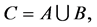 and
and 

Definition 12 [10] If  and
and  are two soft expert sets over U then “
are two soft expert sets over U then “ AND
AND ” denoted by
” denoted by , is defined by
, is defined by
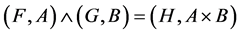
where .
.
Definition 13 [10] If  and
and  are two soft expert sets over
are two soft expert sets over  then “
then “ OR
OR ” denoted by
” denoted by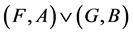 , is defined by
, is defined by

where .
.
3. Fuzzy Soft Expert Set
In this section, we introduce the definition of a fuzzy soft expert set and give basic properties of this concept.
Let U be a universe,  a set of parameters,
a set of parameters,  a set of experts (agents), and
a set of experts (agents), and 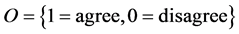 a set of opinions. Let
a set of opinions. Let  and
and .
.
Definition 14 A pair 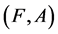 is called a fuzzy soft expert set over
is called a fuzzy soft expert set over  where
where 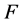 is a mapping given by
is a mapping given by

where  denotes the set of all fuzzy subsets of
denotes the set of all fuzzy subsets of 
Example 1 Suppose that a company produces new types of products and wants to take the opinion of some experts about these products. Let 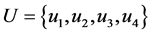 be a set of products,
be a set of products,  is a set of decision parameters where
is a set of decision parameters where  denotes the parameters “easy to use”, “quality” and “cheap”. Let
denotes the parameters “easy to use”, “quality” and “cheap”. Let 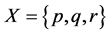 be a set of experts. Suppose that
be a set of experts. Suppose that


















Then we can view the fuzzy soft expert set (F,Z) as consisting of the following collection of approximations:

Definition 15 For two fuzzy soft expert sets  and
and  over
over ,
,  is called a fuzzy soft expert subset of
is called a fuzzy soft expert subset of  if 1.
if 1. 
2. 
 is fuzzy subset of
is fuzzy subset of 
This relationship is denoted by . In this case
. In this case 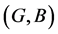 is called a fuzzy soft expert superset of
is called a fuzzy soft expert superset of .
.
Definition 16 Two fuzzy soft expert sets 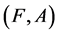 and
and  over U are said to be equal if
over U are said to be equal if  is a fuzzy soft expert subset of
is a fuzzy soft expert subset of  and
and  is a fuzzy soft expert subset of
is a fuzzy soft expert subset of 
Example 2 Consider Example 1. Suppose that the company takes the opinion of the experts once again after a month of using the products. Let

and

Clearly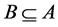 . Let
. Let  and
and  be defined as follows:
be defined as follows:


Therefore .
.
Definition 17 An agree-fuzzy soft expert set  over U is a fuzzy soft expert subset of
over U is a fuzzy soft expert subset of  defined as follows:
defined as follows:

Definition 18 A disagree-fuzzy soft expert set  over U is a fuzzy soft expert subset of
over U is a fuzzy soft expert subset of 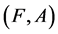 defined as follows:
defined as follows:

Example 3 Consider Example 1. Then the agree-fuzzy soft expert set  over
over 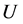 is
is

and the disagree-fuzzy soft expert set 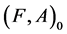 over
over  is
is

Definition 19 The complement of a fuzzy soft expert set  is denoted by
is denoted by  and is defined by
and is defined by  where
where  is a mapping given by
is a mapping given by

where c is a fuzzy complement.
Example 4 Consider Example 1. By using the basic fuzzy complement, we have

Proposition 1 If  is a fuzzy soft expert set over
is a fuzzy soft expert set over  then 1.
then 1. 
Proof From Definition 19 we have  where
where . Now,
. Now,

where 

4. Union and Intersection
In this section, we introduce the definitions of union and intersection of fuzzy soft expert sets, derive their properties, and give some examples.
Definition 20 The union of two fuzzy soft expert sets  and
and  over U, denoted by
over U, denoted by  , is the fuzzy soft expert set
, is the fuzzy soft expert set  where
where  and
and 

where s is an s-norm.
Example 5 Consider Example 1. Let

and

Suppose 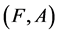 and
and  are two fuzzy soft expert sets over
are two fuzzy soft expert sets over 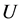 such that
such that


By using basic fuzzy union (maximum) we have  where
where

Proposition 2 If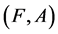 ,
,  and
and  are three fuzzy soft expert sets over
are three fuzzy soft expert sets over , then 1.
, then 1. 
2. 
Proof a. We want to prove that 
By using definition 20 we have

We consider the case when  as the other cases are trivial, then we have
as the other cases are trivial, then we have
 .
.
We also consider her the case when  as the other cases are trivial, then we have
as the other cases are trivial, then we have
 .
.
b. The proof is straightforward.
Definition 21 The intersection of two fuzzy soft expert sets  and
and 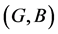 over
over , denoted by
, denoted by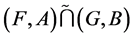 , is the fuzzy soft expert set
, is the fuzzy soft expert set  where
where  and
and 

where t is a t-norm.
Example 6 Consider Example 5. By using basic fuzzy intersection (minimum) we have  where
where

Proposition 3 If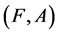 ,
,  and
and  are three fuzzy soft expert sets over
are three fuzzy soft expert sets over , then 1.
, then 1. 
2. 
Proof a. We want to prove that 
By using definition 21 we have

We consider the case when  as the other cases are trivial, then we have
as the other cases are trivial, then we have
 .
.
We also consider her the case when  as the other cases are trivial, then we have
as the other cases are trivial, then we have
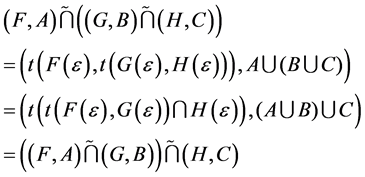 .
.
b. The proof is straightforward.
Proposition 4 If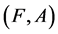 ,
,  and
and  are three fuzzy soft expert sets over
are three fuzzy soft expert sets over , then 1.
, then 1. 
2. 
Proof a. We want to prove that 
By using definitions 20 and 21 we have

We consider the case when  as the other cases are trivial, then we have
as the other cases are trivial, then we have
 .
.
We also consider her the case when  as the other cases are trivial, then we have
as the other cases are trivial, then we have
 .
.
b. We want to prove that 
By using definitions 20 and 21 we have

We consider the case when 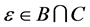 as the other cases are trivial, then we have
as the other cases are trivial, then we have
 .
.
We also consider her the case when  as the other cases are trivial, then we have
as the other cases are trivial, then we have
 .
.
5. AND and OR Operations
In this section, we introduce the definitions of AND and OR operations for fuzzy soft expert sets, derive their properties, and give some examples.
Definition 22 If 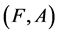 and
and  are two fuzzy soft expert sets over
are two fuzzy soft expert sets over  then “
then “ AND
AND ” denoted by
” denoted by 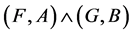 is defined by
is defined by

such that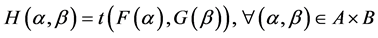 , where t is a t-norm.
, where t is a t-norm.
Example 7 Consider Example 1. Let
 and
and
 .
.
Suppose  and
and  are two fuzzy soft expert sets over
are two fuzzy soft expert sets over  such that
such that
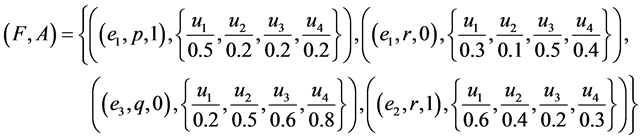

By using basic fuzzy intersection (minimum) we have  where
where
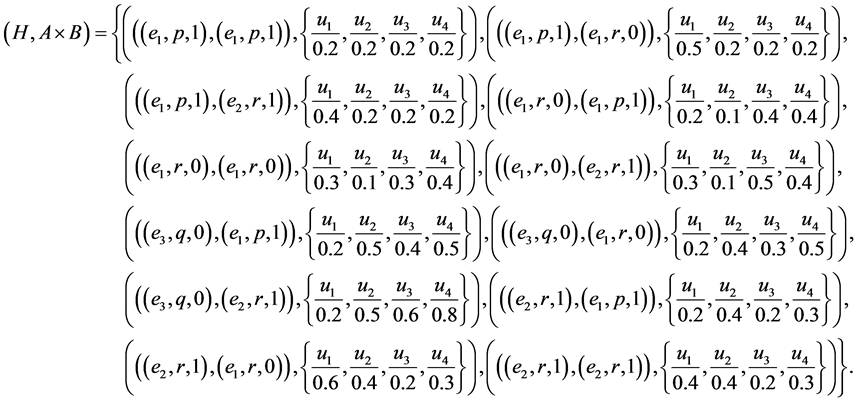
Definition 23 If  and
and  are two fuzzy soft expert sets over U then “
are two fuzzy soft expert sets over U then “ OR
OR ” denoted by
” denoted by  is defined by
is defined by

such that , where s is an s-norm.
, where s is an s-norm.
Example 8 Consider Example 7. By using basic fuzzy union (maximum) we have  where
where

Proposition 5 If  and
and 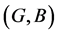 are two fuzzy soft expert sets over
are two fuzzy soft expert sets over 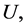 then [a.]
then [a.]
1. 
2. 
Proof a. Suppose that 
Therefore,  Now,
Now,

where 
Now, take 
Therefore,
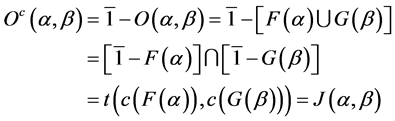 Then
Then  and
and  are the same. Hence, proved.
are the same. Hence, proved.
b. Suppose that 
Therefore,  Now,
Now,

where 
Now, take 
Therefore,
 Then
Then  and
and 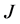 are the same. Hence, proved.
are the same. Hence, proved.
Proposition 6 If ,
,  and
and  are three fuzzy soft expert sets over
are three fuzzy soft expert sets over 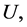 then 1.
then 1. 
2. 
3. 
4. 
Proof We give the proofs of a and b. [a.]
1. Suppose that ,
, .
.
Therefore
 ,
, .
.
 ,
, .
.
 .
.
2. Suppose that ,
,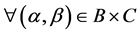 .
.
Therefore
 ,
, .
.
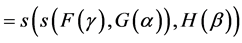 ,
, .
.
 .
.
Remark The commutativity do not hold in AND and OR operations since .
.
6. An Application of Fuzzy Soft Expert Set in Decision Making
In this section, we present an application of fuzzy soft expert set theory in a decision making problem. Assume that a company wants to fill a position. There are four candidates who form the universe  the hiring committee considers a set of parameters,
the hiring committee considers a set of parameters,  the parameters
the parameters  stand for “experience”, “computer knowledge” and “good speaking” respectively. Let
stand for “experience”, “computer knowledge” and “good speaking” respectively. Let  be a set of experts (Committee members). After a serious discussion the committee constructs the following fuzzy soft expert set
be a set of experts (Committee members). After a serious discussion the committee constructs the following fuzzy soft expert set

In Table 1 and Table 2 we present the agree-fuzzy soft expert set and disagree-fuzzy soft expert set respectively.
The following algorithm may be followed by the company to fill the position.
1. Input the fuzzy soft expert set .
.
2. Find an agree-fuzzy soft expert set and a disagree-fuzzy soft expert set.
3. Find  for agree-fuzzy soft expert set.
for agree-fuzzy soft expert set.
4. Find 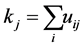 for disagree-fuzzy soft expert set.
for disagree-fuzzy soft expert set.
5. Find 
6. Find m, for which  Then
Then  is the optimal choice object. If
is the optimal choice object. If  has more than one value, then any one of them could be chosen by the company using its option.
has more than one value, then any one of them could be chosen by the company using its option.

Table 1. Agree-fuzzy soft expert set.

Table 2. Disagree-fuzzy soft expert set.
Now we use this algorithm to find the best choice for the company to fill the position. From Table 1 and Table 2, we have the following in Table 3:
Then  so the committee will choose candidate 4 for the job.
so the committee will choose candidate 4 for the job.
7. Mapping on Fuzzy Soft Expert Classes
In this section, we introduce the notion of mapping on fuzzy soft expert classes. fuzzy soft expert classes are collections of fuzzy soft expert sets. We also define and study the properties of fuzzy soft expert images and fuzzy soft expert inverse images of fuzzy soft expert sets, and support them with example and theorems.
Definition 24 Let  be a universe,
be a universe,  a set of parameters,
a set of parameters, 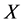 a set of experts (agents), and
a set of experts (agents), and 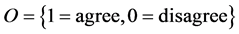 a set of opinions. Let
a set of opinions. Let . Then the collection of all fuzzy soft expert sets over U with a parameters from
. Then the collection of all fuzzy soft expert sets over U with a parameters from  is called a fuzzy soft expert class and is denoted as
is called a fuzzy soft expert class and is denoted as .
.
Definition 25 Let 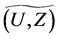 and
and  be fuzzy soft expert classes. Let
be fuzzy soft expert classes. Let  and
and  be mappings. Then a mapping
be mappings. Then a mapping  is defined as follows:
is defined as follows:
For a fuzzy soft expert set 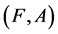 in
in ,
,  is a fuzzy soft expert in
is a fuzzy soft expert in  obtained as follows:
obtained as follows:

For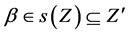 ,
,  and
and .
.  is called a fuzzy soft expert image of the fuzzy soft expert set
is called a fuzzy soft expert image of the fuzzy soft expert set .
.
Definition 26 Let  and
and  be fuzzy soft expert classes. Let
be fuzzy soft expert classes. Let  and
and  be mappings. Then a mapping
be mappings. Then a mapping  is defined as follows:
is defined as follows:
For a fuzzy soft expert set  in
in ,
,  is a fuzzy soft expert set in
is a fuzzy soft expert set in  obtained as follows:
obtained as follows:

For  and
and .
.  is called a fuzzy soft expert inverse image of the fuzzy soft expert set
is called a fuzzy soft expert inverse image of the fuzzy soft expert set .
.
Example 9 Let ,
,  and let
and let
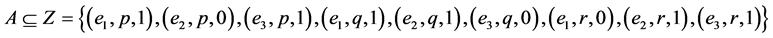
and

Suppose that 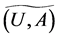 and
and  are fuzzy soft expert classes. Define
are fuzzy soft expert classes. Define  and
and  as follows:
as follows:
 ,
, 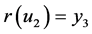 ,
, 


 .
.
Let  and
and  be two fuzzy soft expert sets over U and Y respectively such that
be two fuzzy soft expert sets over U and Y respectively such that


Then we define a mapping  as follows:
as follows:
For a soft expert set 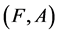 in
in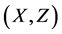 ,
,  is a soft expert set in
is a soft expert set in  where
where
 and is obtained as follows:
and is obtained as follows:
 .
.
 .
.
 .
.
Then 
 .
.
 .
.
 .
.
Then 
 .
.
 .
.
 .
.
Then 
 .
.
 .
.
 .
.
Then 
 .
.
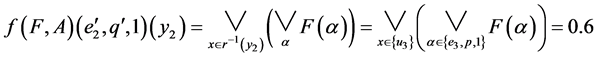 .
.
 .
.
Then 
Hence
 .
.
Next for the soft expert inverse images, the mapping  is defined as follows:
is defined as follows:
For a soft expert set  in
in ,
,  is a soft expert set in
is a soft expert set in  where
where

and is obtained as follows:
 .
.
 .
.
 .
.
Then 
 .
.
 .
.
 .
.
Then 
By similar calculations, consequently, we get

Definition 27 Let 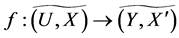 be a mapping and
be a mapping and  and
and  fuzzy soft expert sets in
fuzzy soft expert sets in
 . Then for
. Then for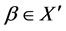 ,
, 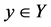 , the fuzzy soft expert union and intersection of fuzzy soft expert images
, the fuzzy soft expert union and intersection of fuzzy soft expert images
 and
and  are defined as follows:
are defined as follows:


Definition 28 Let  be a mapping and
be a mapping and  and
and  fuzzy soft expert sets in
fuzzy soft expert sets in . Then for
. Then for ,
,  , the fuzzy soft expert union and intersection of fuzzy soft expert inverse images
, the fuzzy soft expert union and intersection of fuzzy soft expert inverse images  and
and  are defined as follows:
are defined as follows:


Theorem 1 Let 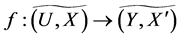 be a mapping. Then for fuzzy soft expert sets
be a mapping. Then for fuzzy soft expert sets 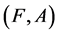 and
and  in the fuzzy soft expert class
in the fuzzy soft expert class , [a.]
, [a.]
1. .
.
2. .
.
3. .
.
4. .
.
5. If , then
, then Proof For (a), (b) and (e) the proof is trivial, so we just give the proof of (c) and (d).
Proof For (a), (b) and (e) the proof is trivial, so we just give the proof of (c) and (d).
c. For  and
and , we want to prove that
, we want to prove that

For left hand side, consider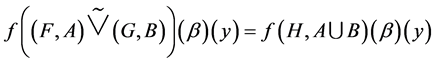 . Then
. Then
 (1.1)
(1.1)
such that  where
where  an interval-valued fuzzy union.
an interval-valued fuzzy union.
Considering only the non-trivial case, then Equation 0.1 becomes:
 (1.2)
(1.2)
For right hand side and by using Definition 27, we have
 (1.3)
(1.3)
From Equations (1.1) and (1.3), we get (c).
d. For 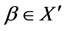 and
and , and using Definition 27, we have
, and using Definition 27, we have
 .
.
This gives (d).
Theorem 2 Let  be mapping. Then for fuzzy soft experts
be mapping. Then for fuzzy soft experts ,
, 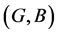 in the fuzzy soft expert class
in the fuzzy soft expert class , we have:
, we have:
1. .
.
2. .
.
3. .
.
4. .
.
5. If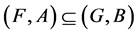 , then
, then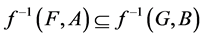 .
.
Proof We use the same method as in the previous proof.
8. Conclusion
In this paper, we have introduced the concept of fuzzy soft expert set which is more effective and useful and studied some of its properties. Also the basic operations on fuzzy soft expert set namely complement, union, intersection, AND and OR have been defined. An application of this theory has been given to solve a decisionmaking problem. We also studied a mapping on fuzzy soft expert classes and its properties.
Acknowledgements
The authors would like to acknowledge the financial support received from Universiti Kebangsaan Malaysia under the research grant AP-2013-009.
NOTES
*Corresponding author.