Two Theoretical Approaches in Solid-State Nuclear Magnetic Resonance Spectroscopy ()
1. Introduction
The time-dependent Schrodinger Equation [1] serves as a benchmark for various theories used in nuclear magnetic resonance (NMR). This time-dependent linear differential Equation (Schrodinger) is the basic framework unifying the quantum mechanical, mathematical physics, quantum chemistry, atomic and molecular physics, quantum electrodynamics, quantum computing or control theory etc., and statistical descriptions of matter [2] - [6] . This framework is the unique one permitting a consistent treatment of the spin dynamics in quantum physics in general and solid-state NMR in particular. Such spin dynamics are central in the description of the quantum measurement process leading to the NMR signal and also in designing sophisticated pulse sequences and understanding of different experiments [7] -[16] .
The main theories used so far in solid-state nuclear magnetic resonance include the average Hamiltonian theory [17] and the Floquet theory [18] -[20] , and the developing theories are the Fer expansion [21] or the FloquetMagnus expansion [22] . These theories provide solutions to the time-dependent Schrodinger Equation which is a central problem in quantum physics in general and solid-state NMR in particular. The expansion schemes of these theories including the Magnus [23] and the Fer expansions can be used as numerical integrators for solving the time dependent Schrodinger Equation. However, there arepotential future theoretical and numerical directions for the calculation of the time propagation and evolution operators use Chebychev expansion [24] -[27] and Cayley method [27] [28] that need further attention in the NMR community.
Computing the exponential of a matrix is an important task in quantum mechanics and in solid-state nuclear magnetic resonance in particular where all theories used rely on exponential Hamiltonian operator propagators. The approximation of the matrix exponential is among the oldest and most extensive research topics in numerical mathematics [27] [29] . This is due to the fact that many physical, biological, and economic processes are governed by mathematical models described by systems of linear, constant coefficient ordinary differential Equations. Although many efficient algorithms have been developed, so far, the problem is still not having being solved in general. For instance, the evaluation of , where
, where  is a (real or complex)
is a (real or complex) 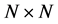 matrix, represents the major factor in the overall computational cost required by this class of algorithms and is probably one of the most problematic aspects. For instance, in the reference [29] , twenty different numerical algorithms for computing the exponential of a matrix are carefully reviewed. Approaches such as scaling and squaring with Pade approximation, Chebyshev approximation, Krylov space methods, or splitting methods, have been used to approach the exponential of a matrix problem [27] .
matrix, represents the major factor in the overall computational cost required by this class of algorithms and is probably one of the most problematic aspects. For instance, in the reference [29] , twenty different numerical algorithms for computing the exponential of a matrix are carefully reviewed. Approaches such as scaling and squaring with Pade approximation, Chebyshev approximation, Krylov space methods, or splitting methods, have been used to approach the exponential of a matrix problem [27] .
Simulation is very important in molecular quantum dynamics especially in the case of chemical exchange or relaxation, where line shapes can be overlapping. The main difficulty encountered in spectrum simulation is the rapid increase of computational requirements with an increasing number of spins. This is due to the exponential scaling of the spin vector space. Specifically, a state of an  spin system is represented by a vector with
spin system is represented by a vector with  dimensions. Therefore, it is essential to establish the most efficient numerical methods for dealing with the very large matrices that result from more challenging simulations. Simulation of spin system dynamics requires the numerical solution of the Liouville von Neumann Equation, or equivalently the numerical exponential of a Liouville matrix [30] .
dimensions. Therefore, it is essential to establish the most efficient numerical methods for dealing with the very large matrices that result from more challenging simulations. Simulation of spin system dynamics requires the numerical solution of the Liouville von Neumann Equation, or equivalently the numerical exponential of a Liouville matrix [30] .
Although the theoretical advantages of the Chebyshev method are still not entirely realized for currently feasible computations, the Chebyshev approach has the potential to be extensively used in spin quantum dynamics and emerged as an important approach for numerical simulations of many systems encounters. Our motivation here is to present the Chebyshev approximation as a potential surrogate of the popular expansions in NMR for the task of numerical simulations in spin dynamics paradigm stems from its numerical stability and high accuracy. In addition to the Chebyshev approximation, we also present the Cayley transformation [31] .
2. Two Potential Future Theoretical and Numerical Directions in Solid-State NMR
2.1. Chebychev Expansion
This new method provides a useful alternative to the exponential mapping relating the Lie algebra to the Lie group. This fact is particularly important for numerical methods where the evaluation of the exponential matrix is the most computation-intensive part of the algorithm. It is noteworthy that the combinations of two or more of the theories known in NMR will continue to provide a framework for treating time-dependent Hamiltonian in quantum physics and NMR in a more efficient way that can be easily extended to all types of modulations.
Nearly three decades ago, Tal-Ezer and Kosloff introduced the Chebyshev method as a means of solving the time-dependent Schrodinger Equation in the field of molecular dynamics [25] . Tal-Ezer shows that the complex Chebyshev polynomials achieve the best approximation to expand the evolution operator. In the Chebyshev approach, the evolution operator  is expended in a truncated series of Chebyshev polynomials. As described in the article [32] , given a function
is expended in a truncated series of Chebyshev polynomials. As described in the article [32] , given a function 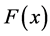 in the interval
in the interval , the Chebyshev polynomial approximations are optimal, in the sense that the maximum error in the approximation is minimal compared to almost all possible polynomial approximations. This procedure is applied by bounding the extreme energy eigenvalues
, the Chebyshev polynomial approximations are optimal, in the sense that the maximum error in the approximation is minimal compared to almost all possible polynomial approximations. This procedure is applied by bounding the extreme energy eigenvalues  and
and  of the Hamiltonian
of the Hamiltonian . Then a truncated Chebyshev expansion of
. Then a truncated Chebyshev expansion of 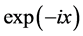 on the interval
on the interval  is considered:
is considered:
 , (1)
, (1)
where
 (2)
(2)
with well-chosen coefficients . The Chebyshev polynomials
. The Chebyshev polynomials  on the interval
on the interval , are determined via the recurrence relation
, are determined via the recurrence relation
 (3)
(3)
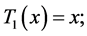 (4)
(4)
 (5)
(5)
which gives the final approximation
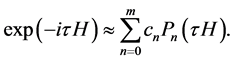 (6)
(6)
The Chebyshev method has two main advantages: first, it exploits the sparsity of the Liouvillian (Hamiltonian) by expressing the propagator in terms of a sequence of  (Liouville superoperator) matrix multiples. The matrix multiples are conveniently performed in terms of a sparse matrix algorithm with storage and compute-time requirements in proportion to the number of nonzero elements of
(Liouville superoperator) matrix multiples. The matrix multiples are conveniently performed in terms of a sparse matrix algorithm with storage and compute-time requirements in proportion to the number of nonzero elements of . Second, the Chebyshev expansion of the propagator is essentially exact. The series converges so rapidly that it is easily extended to the point where the truncation error is smaller than the usual round-off errors expected in any numerical computation. Moreover, the resulting number of terms in the series is at or near the optimally small number for an orthogonal polynomial expansion of the exponential function. The method of Chebyshev approximation is frequently used in numerical quantum dynamics to compute
. Second, the Chebyshev expansion of the propagator is essentially exact. The series converges so rapidly that it is easily extended to the point where the truncation error is smaller than the usual round-off errors expected in any numerical computation. Moreover, the resulting number of terms in the series is at or near the optimally small number for an orthogonal polynomial expansion of the exponential function. The method of Chebyshev approximation is frequently used in numerical quantum dynamics to compute 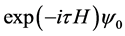 over very long times. This can be done with m matrix-vector products if the above approximation is considered with a sufficiently large truncation index m. The degree m necessary for achieving a specific accuracy depends linearly on the step size
over very long times. This can be done with m matrix-vector products if the above approximation is considered with a sufficiently large truncation index m. The degree m necessary for achieving a specific accuracy depends linearly on the step size  and the spectral radius of
and the spectral radius of , and thus an increase of the step size reduces the computational work per unit step. In a practical implementation, m can be chosen such that the accuracy is dominated by the round-off error [27] . We cannot conclude this section without bringing the attention on existing drawbacks in the Chebyshev method. The scheme is not unitary, and therefore the norm is not conserved, but the deviation from unitarity is very small due to the extreme accuracy of the approach. Another drawback is that because of the long time durations (
, and thus an increase of the step size reduces the computational work per unit step. In a practical implementation, m can be chosen such that the accuracy is dominated by the round-off error [27] . We cannot conclude this section without bringing the attention on existing drawbacks in the Chebyshev method. The scheme is not unitary, and therefore the norm is not conserved, but the deviation from unitarity is very small due to the extreme accuracy of the approach. Another drawback is that because of the long time durations ( is very large) of propagation in the Chebyshev scheme, intermediate results are not obtained. To conclude, despite the above drawbacks, the Chebyshev approach will successfully serve the quantum spin dynamics community in establishing quantum mechanical time dependent methods as a routine tool in quantum dynamics studies.
is very large) of propagation in the Chebyshev scheme, intermediate results are not obtained. To conclude, despite the above drawbacks, the Chebyshev approach will successfully serve the quantum spin dynamics community in establishing quantum mechanical time dependent methods as a routine tool in quantum dynamics studies.
2.2. Cayley Transform
The second approach we are presenting called Cayley transform, provides a useful alternative to the exponential mapping relating the Lie algebra to the Lie group. This fact is particularly important for numerical methods where the evaluation of the exponential matrix is the most computation-intensive part of the algorithm. Blanes and co-workers shown that the solution of the linear ordinary differential Equation can be written as [27]
 (7)
(7)
with  satisfying the so-called dcayinv Equation [28] [31]
satisfying the so-called dcayinv Equation [28] [31]
 (8)
(8)
 is element of the Lie algebra such that if
is element of the Lie algebra such that if  and
and  are also elements of a Lie algebra whose can be combined by the Lie bracket, which we represent by
are also elements of a Lie algebra whose can be combined by the Lie bracket, which we represent by  with the consideration of the orthogonal group, the Cayley transform is
with the consideration of the orthogonal group, the Cayley transform is
 . (9)
. (9)
Note that the choice of  is arbitrary but it ensures, a particularly simple form of various expansion coefficients. Blanes et al. obtained the following time-symmetric methods of order 4 and 6, based on the above Cayley transform,
is arbitrary but it ensures, a particularly simple form of various expansion coefficients. Blanes et al. obtained the following time-symmetric methods of order 4 and 6, based on the above Cayley transform,
Order 4:
 , (10)
, (10)
where
 . (11)
. (11)
Order 6:
 (12)
(12)
Three matrix-matrix products are required in addition to the three commutators involved in the computation of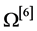 , for a total of nine matrix-matrix products per step. Complete formulation of the scheme is given in the article [33] . It can be seen that the efficiency of Cayley based methods can be built directly from Magnus based integrators. But, unlike Magnus expansions, truncated Cayley expansions do not enjoy the benefits associated with time symmetry. As soon as integrals are replaced by appropriate quadrature formulas, Iserles [31] proved that the time symmetry is gained. The Cayley approach allows employing explicit schemes for solving the differential Equation on the Lie algebra of the group and leads to semi-implicit methods where no iteration is required. The Caley methods in the numerical solution of matrix differential systems on quadratic groups have been applied to many important problems such as the Penrose regression problem (PRP) [34] where this approach has been employed in findind numerical solution of PRP, the calculation of Lyapunov exponents of Hamiltonian systems [35] , the solution of Hamiltonian isospectral problems [36] , etc.
, for a total of nine matrix-matrix products per step. Complete formulation of the scheme is given in the article [33] . It can be seen that the efficiency of Cayley based methods can be built directly from Magnus based integrators. But, unlike Magnus expansions, truncated Cayley expansions do not enjoy the benefits associated with time symmetry. As soon as integrals are replaced by appropriate quadrature formulas, Iserles [31] proved that the time symmetry is gained. The Cayley approach allows employing explicit schemes for solving the differential Equation on the Lie algebra of the group and leads to semi-implicit methods where no iteration is required. The Caley methods in the numerical solution of matrix differential systems on quadratic groups have been applied to many important problems such as the Penrose regression problem (PRP) [34] where this approach has been employed in findind numerical solution of PRP, the calculation of Lyapunov exponents of Hamiltonian systems [35] , the solution of Hamiltonian isospectral problems [36] , etc.
3. Conclusions
We hope this article will encourage the use of Magnus and Fer expansions as numerical integrators as well as the use of Floquet-Magnus expansion as an alternative approach in designing sophisticated pulse sequences and analyzing and understanding of different experiments. We also hope that this letter will contribute to motivating NMR spin dynamics experts to consider other theoretical and numerical perspectives such as Chebyshev or Cayley methods. Although much progress has been made in the theory of NMR compared to other spectroscopic techniques, a lot still needs to be done. So far, the NMR literature does not present theoretical treatment of problems with more than three frequencies analyzed using Floquet theory or Floquet-Magnus expansion approach. With the increase of the level of sophistication of NMR experiments, second and third order terms are of increasing importance, such as in diffusion experiments, or like triple-resonance continuous waves (CW) radio frequency irradiation under MAS. These are some examples of unsolved problems in the theory of NMR. In respect with the developments in the mathematical structure of AHT, FLT, FME, and FE, we expect that the realm of applications of the Floquet Magnus expansion and Fer expansion will also be wide over the years and generate new contributions like the generation of efficient numerical algorithm for geometric integrators [37] -[39] .
The intention of writing this comment is to help bring the current and future prospective theoretical aspects of spin dynamics to the attention of the NMR community and lead new interactions between NMR experts and other specialists in related fields. All of these points strongly support the idea that the Floquet-Magnus expansion, the Fer expansion, and the Chebyshev approach can also be the very useful and powerful tools in quantum spin dynamics.
Acknowledgements
The author acknowledges support from Harvard University/Harvard Medical School, Massachusetts General Hospital, and the National Institute of Health (NIH), under Grants R01-HL110241 and T32 EB013180. The contents of this paper are solely the responsibility of the authors and do not represent the official views of NIH.